高地隙车辆侧倾稳定性主动力矩控制器的研究

余希胜, 冯静安, 王麒淦, 郭祖扬, 喻俊志,2

(1. 石河子大学 机械电气工程学院， 新疆 石河子 832000; 2. 中国科学院 自动化研究所， 北京 100190)

目前,常见车辆大多配备有行驶稳定性控制系统,常见的有制动防抱死系统(anti-lock braking system,ABS)和电子稳定性控制(electronic stability control,ESC)等[1-2].使用车辆稳定性控制的主要目的是为了减少事故受害者人数,其中侧翻类事故导致的死亡率在所有交通事故中约占33%[3].高地隙车辆是与传统车辆相比整车质心更高、离地间隙更大且行驶稳定性更差的特殊作业车辆,高地隙作业车辆具有更易受路面激励以及外部横向激励等不利于整车侧向稳定性的特点[4].同时,在高地隙车辆整车结构中,簧载质量占整车质量比例较大,在作业过程中由于路面激励输入,簧载质量容易发生质心偏移,导致整车发生侧倾甚至导致整车发生侧翻事故,严重影响车辆作业稳定性及驾驶人员的安全性.

与高地隙车辆侧向稳定性控制的相关研究主要集中在车辆工程领域,目前国内外学者对车辆稳定性控制技术进行了大量的理论分析和仿真试验研究.文献[5-6]分别设计了2种基于神经网络的车辆侧倾角状态观测器,能够有效地对车辆侧倾角进行估计,并将估计值用于侧倾稳定性控制系统中.文献[7-8]针对果园作业车的运动特点,设计了主动转向稳定性控制系统,通过仿真模型及比例模型验证了车辆稳定性控制系统的有效性.还有学者[9-10]设计了基于质心侧偏角和横摆角速度等参数反馈的控制器用于车辆稳定性控制系统中.上述研究大都以传统车辆为研究对象,但对于高地隙车辆这种复杂的非线性及时变不确定性的多刚体系统来说,基于质心侧偏角、横摆角速度和直接横摆力矩信息的稳定性控制方法并不适用于在复杂路面条件下高速作业过程中的高地隙车辆.

笔者针对高地隙车辆的复杂作业工况与路面激励导致车辆侧翻等问题,设计一种基于质心侧倾角的主动力矩控制器.建立车辆多体动力学模型,在ADAMS/View中建立动力学物理模型,并基于MATLAB/Simulink建立仿真控制模型,将物理模型与控制模型在Simulink中进行联合仿真.将传统PID控制、模糊PID控制以及灰色模糊PID控制算法分别应用于仿真控制模型中,通过系统响应结果验证仿真模型及控制方法的可行性.

1 高地隙车辆多体动力学建模

1.1 动力学建模

高地隙车辆在田间作业过程中,由于路面状况复杂且多变,影响其行驶及操纵稳定性的主要因素包括质心高度、质心横向位置、车速和悬架侧倾特性等.为分析上述因素对高地隙车辆在颠簸路面上行驶时侧向稳定性的影响,建立只考虑侧倾方向的车辆动力学模型如图1所示.在该模型中,将直角坐标系CGxyz的原点固定于簧载质量的质心CG处,假设车辆簧载质量ms围绕侧倾中心Cr做平面运动,x轴为车辆的纵向,其正方向为前进方向;y轴为车辆的侧向,规定向左为正方向;z轴为车辆的垂直方向,规定向上为正方向.

图1 侧倾动力学模型

根据上述定义,只考虑簧载质量绕x轴的侧倾运动,忽略非簧载质量以及前后轴不同特性对侧倾稳定性的影响,利用达朗贝尔原理建立车辆侧倾动力学模型,假设车辆沿x轴直线行驶,前轮无转向角,根据整车横向力平衡可得

(1)

式中:ay为横向加速度;φ为侧倾角;h为质心到侧倾中心的距离;Ff为前轮侧向力;Fr为后轮侧向力.

由车辆前后轮的线性侧向力模型可得

(2)

式中:kf为前轮侧偏刚度;kr为后轮侧偏刚度;βf为前轮侧偏角;βr为后轮侧偏角.

绕x轴的转矩平衡方程为

(3)

式中:Ix为簧载质量绕x轴的转动惯量;CR为悬架等效侧倾阻尼系数;KR为悬架等效侧倾刚度;g为重力加速度.

将式(1)-(3)联立,可得ay与φ的关系为

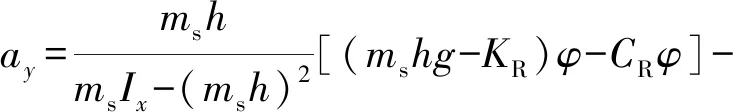
(4)

1.2 控制参数确定

为了保证车辆在行驶过程中稳定地向前行驶,避免发生侧倾甚至侧翻等事故,需要对簧载质量的侧倾角加以控制.控制目标为减小质心侧倾角,防止产生过度的倾覆力矩使整车侧翻,添加控制力矩后的平衡方程可由转矩平衡以及动能定理得到,即

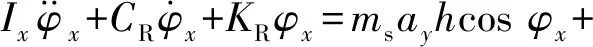
(5)

式中:φx为施加控制力矩后的质心侧倾角.

假设在施加主动控制力矩M前后质心速度均为0,根据机械能守恒定律进行动力学分析,可得

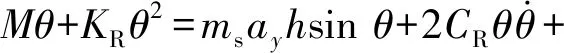
(6)

式中:θ为施加控制力矩后转过的角度,θ=φ-φx.

当φx=0时,即控制力矩使负载回到初始平衡位置,考虑到φ非常小,sinθ≈θ,cosθ≈1,式(6)经简化可得M与φ的关系,即

(7)

将式(5)代入式(7),可得主动控制力矩模型为

(8)

由于高地隙车辆宽高比较小且质心较高,在侧倾失稳状态下,横摆角的变化相对于侧倾角的变化更小,故可将式(8)简化为

(9)

式(9)即为高地隙车辆上侧倾稳定性控制参数的主动控制力矩M与侧倾角φ的关系式.

2 车辆仿真建模

为了对高地隙车辆行驶在复杂路况下的运动状态进行仿真模拟,验证控制方法的合理性与有效性,利用ADAMS/View建立整车的物理模型以及轮胎与路面模型,并基于MATLAB/Simulink搭建侧倾稳定性控制系统联合仿真模型,进行同步计算,并通过预先定义的ADAMS与MATLAB的输入输出接口在每一个仿真步长内进行数据通讯.

2.1 整车模型

虚拟样机技术是当前解决工程应用问题的一门主流技术,其涉及多体系统动力学等诸多学科.它利用软件建立虚拟样机模型和动力学模型,结合研发人员的实践经验,为解决工程应用问题提供参数依据[10].在利用ADAMS/View进行建模时,为了不影响动力学分析准确度的基础上,对结构复杂的实际样机进行一定的结构简化,以提高建模与仿真分析的效率,建立的虚拟样机模型如图2所示.

图2 虚拟样机模型

为了实现侧倾稳定性控制,需要在模型中对模型进行输入输出变量设置.液压缸的主动力设置为输入变量;质心侧倾角、侧倾角速度设置为输出变量.在ADAMS中利用ADAMS/control插件建立ADAMS与MATLAB的数据通讯接口,在进行联合仿真时,由Simulink的控制器模型计算出的主动力控制信号,联合仿真时,通过预先定义的数据通讯接口将输入变量实时传递给ADAMS中的车辆模型.

建立的高地隙车辆动力学模型主要考虑簧载质量的侧倾运动,通过查阅资料、图纸、计算等方法可确定其模型参数,建立的整车虚拟样机模型中前轮轴至后轮轴之间的距离为3.0 m, 两侧轮胎之间的轮距为2.0 m, 车辆离地间隙高度为1.5 m, 整车质量为536.31 kg,簧载质量为275.95 kg, 簧载质量质心与侧倾中心距离为0.3 m, 簧载质量绕侧倾中心的转动惯量为308.36 kg·m2, 悬架等效侧倾刚度为4 000 N·s·rad-1, 悬架等效侧倾阻尼系数为20 N·s·rad-1.

2.2 轮胎及路面模型

ADAMS软件内置多种轮胎模型,不同轮胎模型适用于不同的工作范围,可根据不同工况进行选择.高地隙车辆受到随机路面激励输入,对行驶在复杂路况条件下的车辆进行操纵稳定性分析时,需要能够适应复杂路面的轮胎模型才能得到较为准确的分析结果.选用Fiala轮胎模型,其轮胎质量为20 kg,轮胎自由半径为0.38 m,轮胎宽度为0.21 m,轮胎扁平比为0.55,轮毂半径为0.20 m,轮毂宽度为0.17 m,轮胎垂向刚度为190 000 N·m-1,轮胎垂向阻尼系数为50 N·s·m-1,轮胎静摩擦与动摩擦系数分别为0.8和1.1.

模拟随机路面的模型建立方法由很多种,主要方法有滤波白噪声生成法、谐波叠加法以及随机序列生成法等.为了最大程度上模拟随机路面激励输入,采用谐波叠加法生成随机路面时域模型.依据随机路面构造的谐波叠加法原理和路面功率谱密度Gq(n)的拟合表达式,利用MATLAB软件编制能够生成A-H 这8个等级的三维随机路面谱程序,根据高地隙车辆的工况要求,建立路面较为复杂的E级斜坡路面,然后,在MATLAB软件中生成符合ADAMS仿真要求的随机路面,导出为rdf格式文件,以供导入ADAMS轮胎路面模型仿真使用,经过多次测试验证,该路面模型能够满足虚拟样机路面激励的仿真要求.

2.3 基于PID控制算法的控制模型

(10)

KI=KP/TI,

(11)

KD=KPTD,

(12)

式中:M(t)为t时刻施加的主动控制力矩;KP,KI,KD分别为比例、积分、微分控制参数;Δφ(t)为t时刻的质心侧倾角偏差量;TI为积分时间常量;TD为微分时间常量.

3 仿真试验

将建立的物理模型与仿真控制模型在MATLAB/Simulink中进行联合仿真,在建立的随机路面条件下对设计的PID控制器、模糊PID控制器以及灰色预测模糊PID控制器进行仿真试验并比较这3种控制器的响应结果.

3.1 PID控制器仿真试验

在侧倾稳定性控制系统中,PID控制器根据传感器输入的侧倾角与期望的侧倾角之间的偏差,对负载施加合适的主动控制力矩,实现在系统控制参数不变条件下对侧倾角的控制.在PID控制系统中,比例环节能够快速减小响应偏差,在调节的同时易产生稳态偏差,积分环节可以消除系统稳态偏差,因此比例环节常与积分环节配合使用,微分环节起一定预测作用,在控制系统中可以不使用,常见有PI或PID这2种控制器.基于MATLAB/Simulink建立的PID仿真控制模型如图3所示.

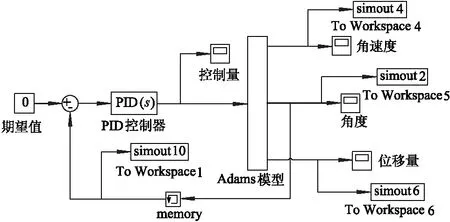
图3 PID仿真控制模型

图3中PID控制器根据输入的侧倾角偏差输出响应的主动控制力矩M,其中,PID控制参数整定的方法有很多,这里采用试凑法,反复调整PID控制参数,最终确定控制参数如下:KP=2;KI=2.4;KD=2.4.经过验证,这组参数能够使控制系统取得最优的控制效果.系统仿真结果如图4所示.

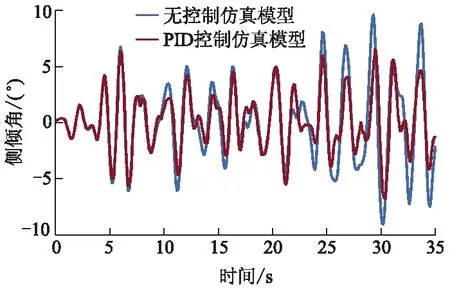
图4 PID控制与无控制响应对比

从图4可以看出:无控制器作用时,质心侧倾角波动范围为-9.34°～9.05°,在随机路面激励下很可能会出现侧翻危险,而在增加PID控制器后,质心侧倾角波动范围为-6.36°～6.46°,侧倾角变化范围减小了30.3%,侧倾角平均值增加了0.024°,同时反映响应曲线波动程度的均方根值(RMS)减小了29.4%,在一定程度上保证了高地隙车辆行驶时的操纵稳定性,证明了PID控制器的可行性与有效性,但增加PID控制器后车辆质心侧倾角依然较大,PID控制器的控制效果有限,需要进一步研究.

3.2 模糊PID控制器仿真试验

模糊PID控制是基于PID控制算法的一种智能控制方法.PID控制算法能够对侧倾角控制起到一定作用,但PID参数固定,在随机波动程度较大的路面激励条件下,对于复杂的时变系统无法起到很好的控制效果.加入模糊控制算法后,根据制定的模糊规则可对PID参数进行自正定,根据系统响应结果自行调整PID参数以起到更好的控制效果.高地隙车辆侧倾稳定性控制系统中的模糊PID控制器通过传感器不断检测侧倾角以及侧倾角速度偏差,利用模糊控制规则在线对PID参数进行整定,使高地隙车辆行驶时具有良好的操纵稳定性.模糊PID的控制原理图如图5所示.

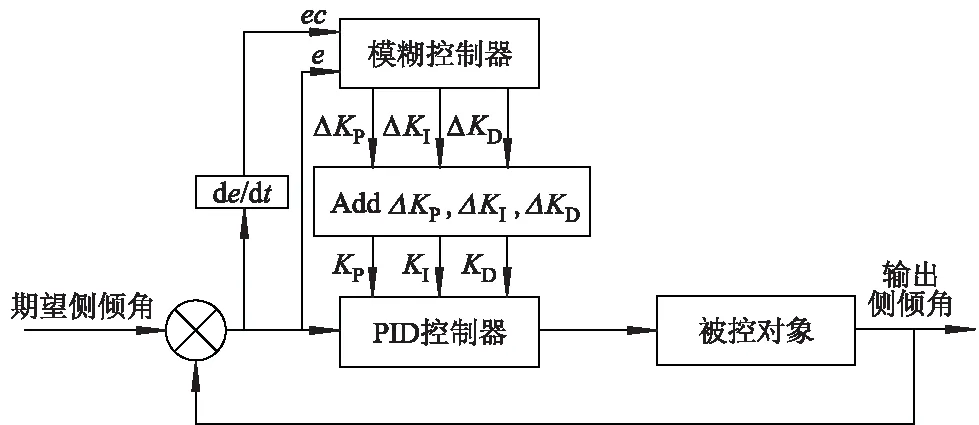
图5 模糊PID控制器原理图

根据模糊PID控制原理,通过测得当前侧倾角以及侧倾角速度偏差,利用已制定好的模糊规则推理,制定PID控制参数的模糊推理规则表.侧倾角论域为{-10,0,10},侧倾角速度论域为{-1,0,1},PID参数中KP论域为{-2,0,2},KI,KD论域均为{-2.5,0,2.5},这5个变量的模糊子集均定义为{NB,NM,NS,ZO,PS,PM,PB},从而得出各模糊子集的隶属度函数.采用中心法进行解模糊后,可得PID控制参数与侧倾角偏差e、侧倾角速度偏差ec的关系曲面如图6所示.

图6 PID控制参数与侧倾角偏差、侧倾角速度偏差的关系曲面图

根据建立的模糊控制规则与PID控制器结合,将基于Simulink建立的PID控制器模型与模糊控制器组成联合控制模型,随设计的模糊PID控制器进行仿真.得到控制系统的仿真模型如图7所示.PID模块的初始参数值设定为KP=2,KI=0.1,KD=0.1,由于加入模糊控制器的原因,初始参数值与普通PID控制器的参数值有所不同.模糊PID控制系统的响应曲线如图8所示.

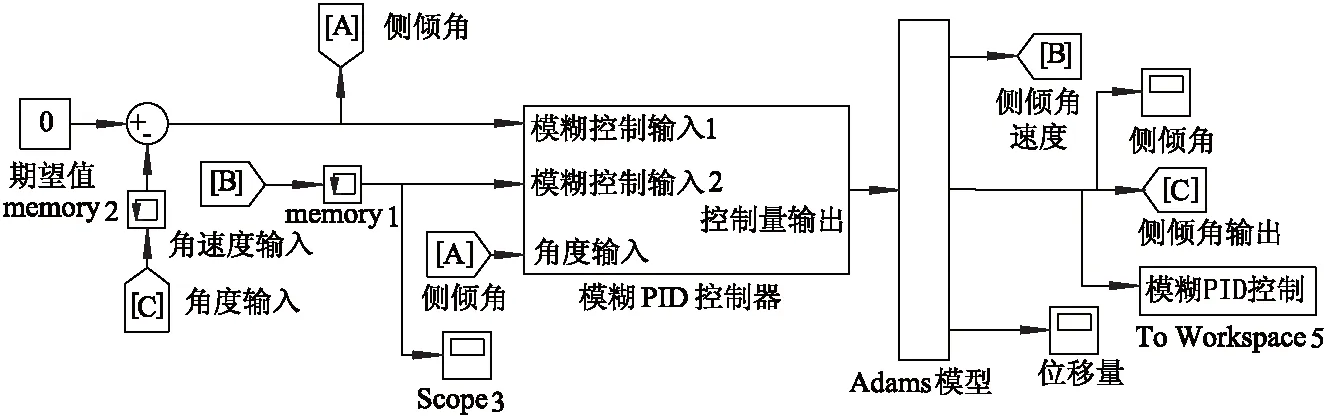
图7 模糊PID控制器仿真控制模型

图8 模糊PID控制器响应曲线

从图8可以看出:模糊PID控制器与PID控制器的响应曲线形状相似,峰值不同,波动程度不同,模糊PID控制器作用效果明显;基于PID控制算法,添加模糊控制后,侧倾角变化范围由-6.36°～6.45°减小至-5.57°～6.16°,波动范围减小了8.49%,模糊PID控制与PID控制器相比,控制效果有一定的改进;反映控制响应曲线波动程度的均方根值减小了17.5%,模糊PID控制器的响应曲线更加平稳,能更好地保证高地隙车辆的侧倾稳定性,模糊PID控制器对于高地隙车辆侧倾稳定性的控制有进一步的改进,但改进程度较小,响应曲线波动依然较大,若能进一步缩小响应曲线波动程度与侧倾角的曲线峰值,将能够更好的保证高地隙车辆的侧倾稳定性.

3.3 灰色模糊PID控制器仿真试验

设计的PID控制器以及模糊PID控制器均是根据系统已发生的行为特征进行控制,属“事后控制”.此类控制方法在多数情况下对于系统控制有效,但由于系统的惯性,很难完全做到真正的实时控制,因而对于系统的控制质量有限.由邓聚龙[11]提出的灰色预测控制理论,则是从系统行为的原始数据中寻找规律,并对系统的未来行为做出预测,根据预测结果做出相应的控制决策.

基于普通PID控制以及模糊PID的优缺点,将灰色预测控制方法与模糊PID控制策略相结合,利用灰色预测模型对系统行为进行预测的优点,配合模糊PID控制算法整定PID控制参数.取建模维数n=4,灰色预测的预测步数取N=1,建立等维新息GM(1,1)灰色预测模型,根据采集的4个系统原始侧倾角偏差以及侧倾角速度偏差数据,将数据经过累加求和以消除随机误差,并得出白化方程后求出在k时刻的解,并预测(k+N)时刻侧倾角偏差量,将预测得到的偏差量用于控制,灰色模糊PID控制原理图如图9所示.

图9 灰色模糊PID控制器原理图

图9中,基于Simulink通过S-Function建立灰色预测模型并编制相应的M文件,将建立的灰色预测模型添加到灰色模糊PID控制模型反馈回路中,利用当前时刻以及前3个采样周期的数据,由灰色预测算法求得下一时刻的预测值,将预测值取代当前侧倾角偏差以及侧倾角偏差变化并用于模糊PID的参数在线整定,建立的Simulink控制模型如图10所示.基于图10中的灰色模糊PID控制器模型进行联合仿真,通过仿真试验,确定PID控制参数初始值为KP=2.09,KI=0.25,KD=0.1,取仿真周期T=35 s,可得系统仿真结果如图11所示.

从图11可以看出:在反馈回路中增加灰色预测模型后的模糊PID控制器与模糊PID控制器的响应曲线形状大致相似,只是峰值与曲线波动程度有所减小,灰色预测模糊PID控制器对于高地隙车辆质心侧倾角的控制效果比模糊PID控制器的效果有进一步的改善;基于模糊PID控制器,添加灰色预测模型后,侧倾角变化范围由-5.57°～6.16°减小至-4.93°～5.09°,波动范围减小了14.6%,可见灰色预测模糊PID控制器对于模糊PID控制器相比于模糊PID控制器对于PID控制器的响应效果有更大的改善,这是因为灰色预测模型的加入使得控制器能够提前预测系统响应并发出相应控制指令,得到更好的控制效果;反映控制响应曲线波动程度的均方根值减小了5.94%,说明灰色预测模型对于响应曲线的波动程度有进一步的改善,灰色预测模糊PID控制器相比于PID控制器与模糊PID控制器,能更好地控制高地隙车辆侧倾角变化,也能在最大程度上保证车辆行驶时的侧倾稳定性与操纵稳定性.

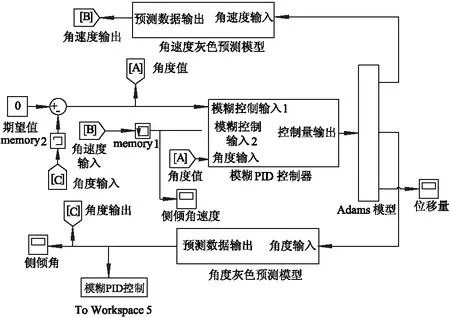
图10 灰色模糊PID控制器仿真控制模型

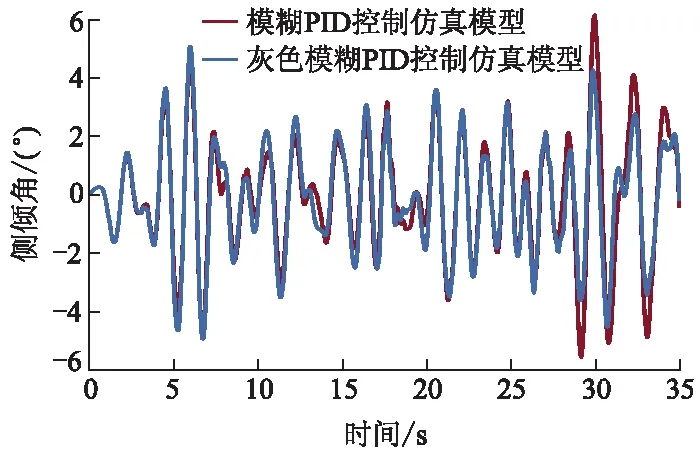
图11 灰色预测模糊PID控制器响应曲线

3.4 控制器效果对比

将无控制器仿真模型、PID控制器仿真模型、模糊PID控制器仿真模型以及灰色模糊PID控制器仿真模型的控制结果进行对比,结果如表1所示.

从表1可以看出:无控制模型作用时,由于建立的路面模型随机程度大,侧倾角变化范围较大,波动程度剧烈;加入PID仿真控制器模型后,质心侧倾角变化范围减小了30.3%,响应曲线均方根值减小了29.4%,具有较明显的控制效果;在PID仿真控制模型的基础上,加入具有在线整定PID参数的模糊控制算法,使PID控制参数不再固定不变,而是可以根据相应情况进行在线整定,使得质心侧倾角变化范围减小了36.2%,侧倾角响应曲线均方根值减小了41.7%;在模糊PID仿真控制模型的基础上,加入灰色预测模型,起到“事前调节”的作用,质心侧倾角变化范围减小了45.5%,响应曲线均方根值减小了45.2%;3种控制器的作用有效程度依次为灰色预测模糊PID控制器、模糊PID控制器、PID控制器.

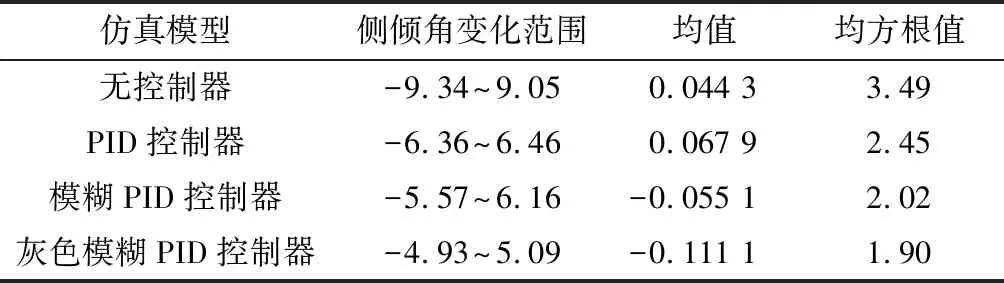
表1 不同控制器的控制效果对比 (°)

4 结 论

1) 结合高地隙车辆复杂作业工况分析,建立了高地隙车辆整车动力学模型及轮胎与路面模型,在动力学分析基础上,建立侧倾角主动力矩及控制模型,为实现高地隙车辆在复杂路面、低速行驶过程中侧倾稳定性控制提供理论依据.

2) 将ADAMS/View与MATLAB/Simulink中建立的模型相结合,进行联合仿真分析.基于PID控制算法的原理,结合模糊控制算法与灰色预测控制的优点,建立了模糊PID仿真控制模型以及灰色模糊PID仿真控制模型,应用于联合仿真模型的控制系统中,分别验证不同控制算法对于质心侧倾角控制的控制效果,并进行比较.通过联合仿真结果分析,利用不同控制算法的控制系统具有不同的控制效果,其中灰色模糊PID控制算法的效果最优,表明主动力矩控制系统能够对质心侧倾角进行有效控制.