基于稳定性的DEV分层控制策略研究

赵 涛，李 强，邢紫筱，吴 坚

(1.浙江科技学院 机械与能源工程学院，杭州 310023；2.爱丁堡大学 工程学院，爱丁堡 EH8 9YL)

分布式驱动电动汽车(distributed-driven electric vehicle，DEV)精简了底盘结构，具有结构紧凑、传动效率高、动力分配灵活等优点。它能够充分利用DEV的驱动力和制动力可独立调节分配的优势，挖掘电动汽车在不同路面状况下的附着力潜力，从而提高其动力性和经济性，改善其操纵性能。

DEV一般都是通过感知当前车辆状态，采用智能控制策略来获得所需的期望横摆力矩，如采用滑模控制理论对车辆横摆角及质心侧偏角进行联合控制[1-2]；基于EKF(extended Kalman filter，扩展卡尔曼滤波器)估计车速后对车辆进行直接横摆力矩控制，在一定程度上提高了轮胎的纵向利用率[3]；以轮胎附着利用率最小化为优化目标函数控制横摆补偿力矩，从而改善了车辆的转向动态特性[4-5]；基于模糊控制和滑模滑转率控制策略，当滑转率超过设定阈值时将直接限制驱动转矩，提高了车辆在低附着路面的驱动防滑效果[6-8]。采用智能控制策略有较好的操纵稳定控制效果，但有些参数的设定需要大量的专家经验，有些控制算法相对较为复杂，不利于实时控制。针对分布式独立驱动电动汽车的转矩分配问题，我们采用简化滑转率控制方法设计了基于稳定性分层的转矩控制器，分别在高、低附着路面上对直行和转弯等不同行驶工况进行仿真验证，以期提高DEV驱动防滑性能及转向操作稳定性。

1 整车动力学模型

1.1 车身动力学模型

图1 七自由度整车动力学模型

选取沿x轴的纵向运动、沿y轴的横向运动、绕z轴的横摆运动及4个轮胎的运动[9]，建立用于DEV转矩分配的七自由度整车动力学模型，如图1所示。

整车动力学方程为

(1)

(2)

(3)

(4)

式(1)～(4)中：m为整车质量，kg；vx、vy分别为车辆纵向和横向速度，m/s；δ、ω分别为前轮转角和车身横摆角速度，rad，rad/s；Fxij、Fyij分别为车辆所受纵向力、横向力，N，其中i=f、r，表示前、后车轮，j=l、r，表示左右车轮(i、j下同)；lf、lr、lw分别为车辆质心到前、后轴的距离及车辆后轮距，m；Iz为车辆横摆转动惯量，kg·m2；β为质心侧偏角，rad。

1.2 轮胎动力学模型

轮胎作为汽车与地面接触的唯一零部件，其力学性能和结构直接影响了汽车的各项性能。采用精度较高的Dugoff轮胎动力学模型[10-11]，运用摩擦圆的概念来计算组合的纵向力和横向力，相比于魔术轮胎动力学模型，Dugoff模型使用更少的系数，便于嵌入式MCU进行快速计算。轮胎的动力学方程为

(5)

式(5)中：Fxij、Fyij、Fzij分别为轮胎所受纵向力、横向力和垂向力，N；Cx、Cy分别为轮胎的纵向、横向刚度，N/m；hg为质心离地高度，m；ax、ay分别为纵向加速度和横向加速度，m/s2。当i=f，r时，li=lr，lf；当ij=fl，fr，rl，rr时，运算符±分别表示-+、--、++、+-。其中

(6)

式(6)中：αf、αr分别为前后轮的侧偏角，rad；各驱动轮滑转率

(7)

式(7)中：ωwir为车轮角速度，rad/s；R为轮胎的动载半径，m；ωwij为各驱动电机转动角速度，rad/s；各驱动轮中心速度

(8)

式(8)中：当ij=fl，rl时，运算符±表示+-；当ij=fr，rr时，运算符±表示-+。

1.3 轮毂电机模型

图2 驱动轮运动受力模型

针对驱动防滑问题对矢量控制电机进行简化，结合轮胎动力学模型，驱动电机负载转矩[12]为

(9)

式(9)中：Tcij为电磁转矩，Tdij为各电机的负载转矩，N·m；c为驱动轮阻尼系数，N/(m·s-1)；Id为电机转子转动惯量，kg·m2。驱动轮运动受力模型如图2所示，由图可得各驱动轮的转矩平衡方程为

(10)

式(10)中：Iwij为各驱动轮的转动惯量，kg·m2。

2 设计分层控制器

2.1 控制系统结构

以驾驶员输出转矩(即踏板开度)作为总的控制器输出约束，由上层集中控制器依据当前车辆模型实时反馈的车身横摆角速度等状态信息，计算车辆当前所需的实际总转矩并分配至各驱动轮，以使车辆由转向引起的横摆角速度变化得到控制；下层控制器以各驱动轮的理想滑转率为控制目标，对车辆反馈的各驱动轮滑转率进行实时监测，由PID控制器计算出各驱动轮保持理想滑转率所需的补偿转矩，结合上层集中控制器分配至各驱动轮的转矩，从而确定最终分配至驱动轮的实际转矩。整车转矩分配分层控制策略如图3所示。

图3 整车转矩分配分层控制策略

2.2 上层集中控制器——驱动总转矩及分配

由二自由度整车参考模型得到控制系统的期望横摆角速度。集中控制器的控制目标为整车横标角速度保持在期望横摆角速度值附近，以使车辆保持良好的操纵稳定性和舒适性[13]。建立二自由度整车模型的数学模型为

(11)

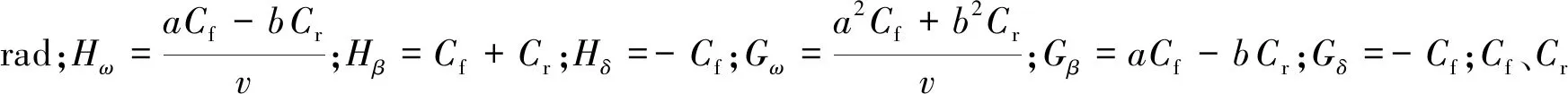
由式(3)、(11)可得期望横摆角速度与实际横摆角速度ω之差

Δω=ωr-ω。

则由Δω产生的附加横摆力矩ΔM=IzΔω，至此计算出需要对驱动轮进行分配的转矩差。为了单独研究驱动力转矩控制对车辆稳定性的影响，图1车辆向右转弯时，施加在各驱动轮的驱动转矩分别为

(12)

式(12)中：Tm为驾驶员期望的输出转矩，N·m。

2.3 下层滑转率控制器——各驱动轮的起步修正转矩计算

建立在各驱动力驱动电机的输出转矩已知的条件下，即上层控制器对各驱动轮进行转矩预分配后，分别研究各驱动轮的滑转情况并最终得出修正转矩。当驱动车轮滑转率从0开始增加时，驱动力也随之增加；当最佳滑转率达到15%～23%时，驱动力达到最大值；如果滑转率继续增加，驱动力则会下降。车辆滑转率过高，不仅无法正常行驶还会加剧轮胎磨损甚至失去操纵稳定性；滑转率过低则无法充分利用路面的附着力，致使车辆动力性较差。考虑到车辆驱动防滑控制，即轮滑转率控制在最优滑转率附近，当车辆实际滑转率超过最优滑转率时，降低驱动电机的输出转矩以减轻车轮的滑转程度[14-15]。为方便研究，以左前轮为例对量符号下角标进行简化，记各驱动轮滑转率为S，驱动轮纵向附着力为Fx，驱动力矩为Td，μx为纵向力附着系数，得

(13)

式(13)中：Fx为轮胎的驱动力，N，其最大值称为附着力，由轮胎载荷Fz和纵向峰值附着系数μxmax共同决定。纵向附着系数μx与滑转率S的数学关系式为

(14)

式(14)中：μp为纵向峰值系数；μs为滑动附着系数；Sp为最佳滑转率。

横向附着系数μy与滑转率S的数学关系式为

μy=μm(1-S)。

(15)

式(15)中：μm为横向峰值系数。

滑转率控制器以实时滑转率偏差值ΔS(t)为输入参数，输出参数为驱动电机的补偿转矩Tsij。本文控制算法旨在对车辆主要参数实现良好的跟踪性能，对操作条件的变化具有较强的适应性；同时，该控制器应易于实施且具有较快的频率响应特性，以利于车辆的实时控制。根据PID控制规则[16]得

(16)

式(16)中：KP、KI、KD分别为控制器比例参数、积分参数、微分参数。

3 整车控制系统的搭建及仿真

基于转矩矢量控制系统模型及整车动力学模型，分别在以下路况进行仿真分析：在高附着路况和低附着路况下进行启动加速试验；在高附着路况进行不同转弯工况稳定性试验。整车部分参数见表1。

表1 整车部分参数

3.1 低附着路况下的启动防滑仿真分析

当车辆在冰雪路况原地起步时，取一个驱动轮的仿真结果进行对比分析，如图4～6所示。

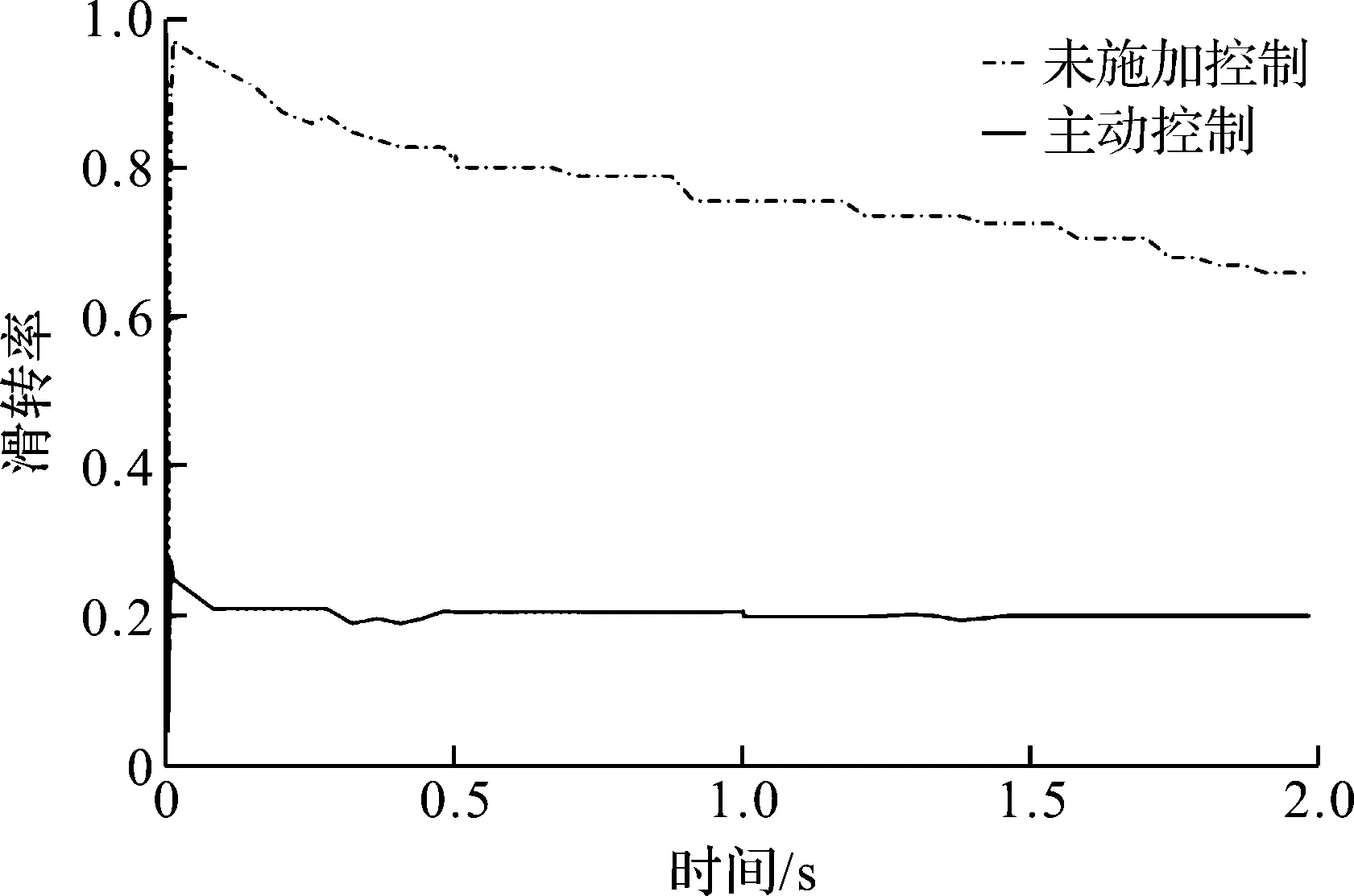
图4 低附着路况下启动时滑转率对比

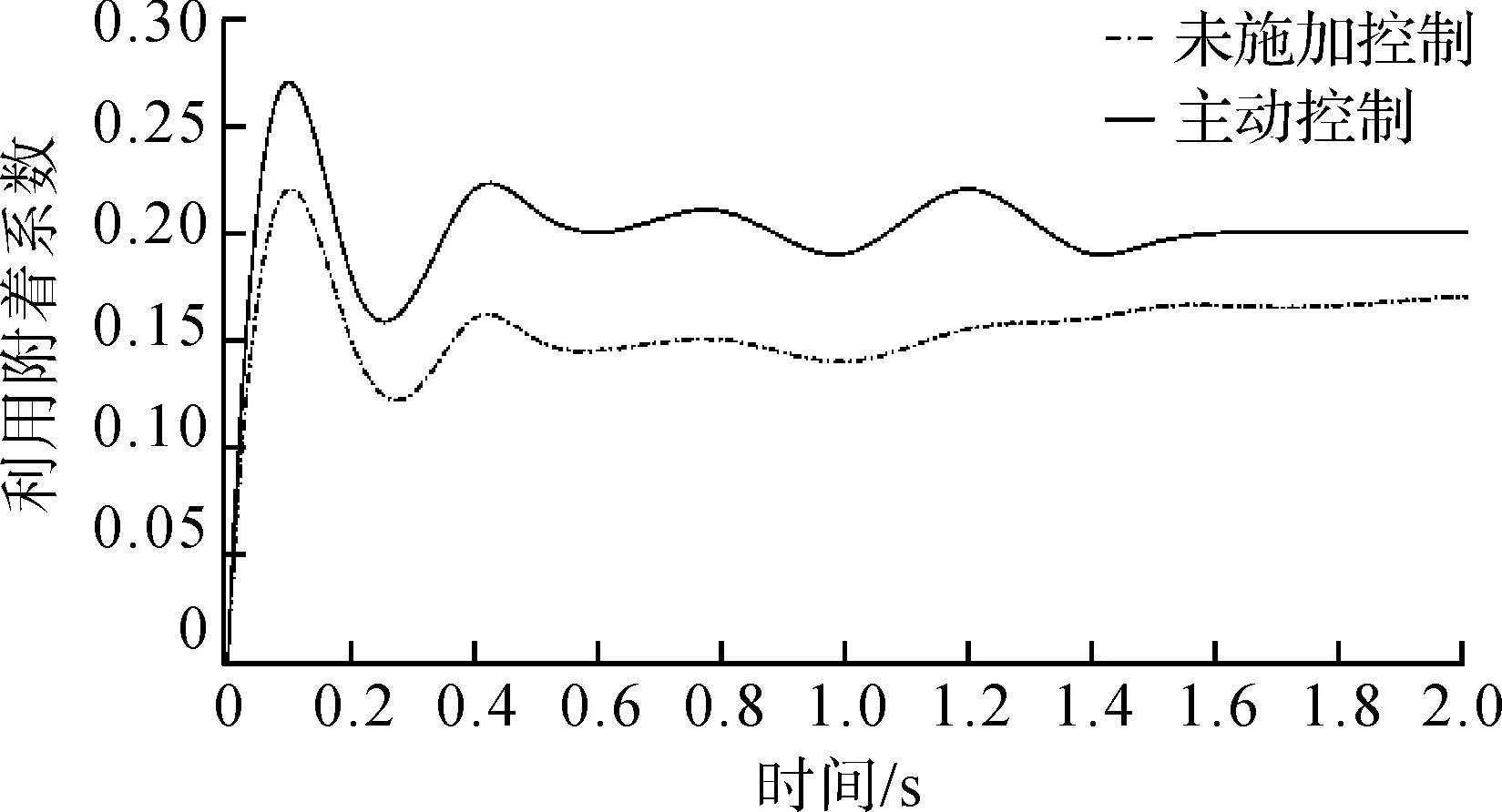
图5 低附着路况下利用附着系数对比

图6 低附着路况下车身加速度对比

由图4可知，当车辆在附着系数很低的冰雪路面进行起步时，未施加控制时的驱动轮出现严重的过度滑转，此时轮胎磨损加剧同时动力性降低，滑转率接近0.97，随后逐渐降低但仍然在0.65以上；施加主动分配控制后，启动时的过度滑转现象得到有效的抑制，驱动轮滑转率基本上维持在0.21左右，可见本文算法介入时间较短。由图5可知，利用附着系数也得到一定的改善。图6中采用主动控制后车身加速度稳定在1.2 m/s2，较未施加控制时的车身加速度也有所改善，能保证车辆具有良好的动力性和操纵性。

3.2 对接路面下仿真分析

图7 对接路面下仿真结果

车辆从附着系数为0.5的碎石路面启动，0.8 s后进入附着系数为0.2的冰雪路面，其他条件同3.1。仿真结果如图7所示。由图7可知，未施加控制的车辆在0.8 s时，由于进入附着系数较低的冰雪路面立即发生严重的打滑现象，滑转率激增至0.6左右。车辆的利用附着系数也骤降至0.18，随后缓慢下降。施加主动控制的车辆滑转率并未发生明显变化，保持在最佳滑转率0.17左右[16](由路面附着系数与滑转率关系得出)，同时利用附着系数也保持在0.18左右。

3.3 对开路面下仿真分析

车辆左侧车轮行驶在附着系数为0.5的碎石路面上，右侧车轮行驶在附着系数为0.2的冰雪路面上，其他条件同3.1，取左前轮和右前轮为研究对象，仿真对比分析结果如图8～9所示。

图8 对开路面下滑转率对比

图9 对开路面下利用附着系数对比

由图8～9可知，未施加控制的车辆左前轮在冰雪路面启动时发生严重的过度滑转，滑转率达0.91；随后车辆滑转率逐渐下降，利用附着系数维持在0.15以内，车辆右前轮滑转率在0.18左右，接近路面利用附着系数，此时车轮可能发生激转现象，处于危险状态。施加主动控制后的车辆启动时的过度滑转得到抑制，车辆左前轮、右前轮滑转率均维持在0.17左右，充分利用了路面附着力，且处于冰雪路面的左前轮利用附着系数也有一定的提高。

3.4 在高附着路况进行不同转弯工况的仿真分析

车辆行驶在附着系数为0.8的路面上，车速为60 km/h，在单移线工况和阶跃输入工况下的横摆角速度仿真对比分析结果如图10～11所示。在图10中，当车辆在附着系数为0.8的路面上以60 km/h的速度超车时，经主动分配转矩后的车辆横摆角速度响应曲线(虚线)可以很好地跟踪参考横摆角速度响应曲线(实线，由二自由度模型得出)，但未施加控制的车辆横摆角速度响应曲线与参考曲线偏差较大。在图11中，当车辆在附着系数为0.8的路面上以60 km/h的速度转弯时，横摆角速度响应的对比结果与单移线工况下相似，可见使用分层控制器后车辆的操纵稳定性得到较大的改善。

图10 单移线工况下的横摆角速度

图11 阶跃输入工况下的横摆角速度

4 结 语

本研究通过采用分层控制策略，对整车的横摆角速度和驱动轮的滑转率进行综合控制，较好地解决了DEV车辆的四轮转矩协调分配问题。上层集中控制器采用二自由度车辆模型求期望横摆角速度，再与七自由度车辆模型中的横摆角速度之差作为控制目标，完成整车横摆力矩的预分配；下层PID滑转率控制器则实现驱动轮的转矩补偿控制。对车辆在不同附着路面进行启动驱动防滑试验及高速转弯试验的结果表明，我们设计的方法可以实现对理想横摆角速度和理想滑转率的跟踪，在充分发挥动力性的同时还保证了DEV车辆的行驶稳定性。