注重策略对比 深度发展思维

○申武广

众所周知，运算定律向来是计算教学的重点和难点，如何能够正确且灵活地运用运算定律，是我们课堂教学中密切关注的问题。在教学四年级下册第三单元运算定律的最后一课即《解决问题策略的多样化》时，教师讲完例题之后依次出示了两道教材上的练习题，引发了学生的热烈讨论。

【案例呈现】

先出示72×125，独立思考后，学生展示各自的解法：

经过讨论，学生普遍认为后两种方法比较简便。然后接着做第二道题88×125，学生的解题方法更多：

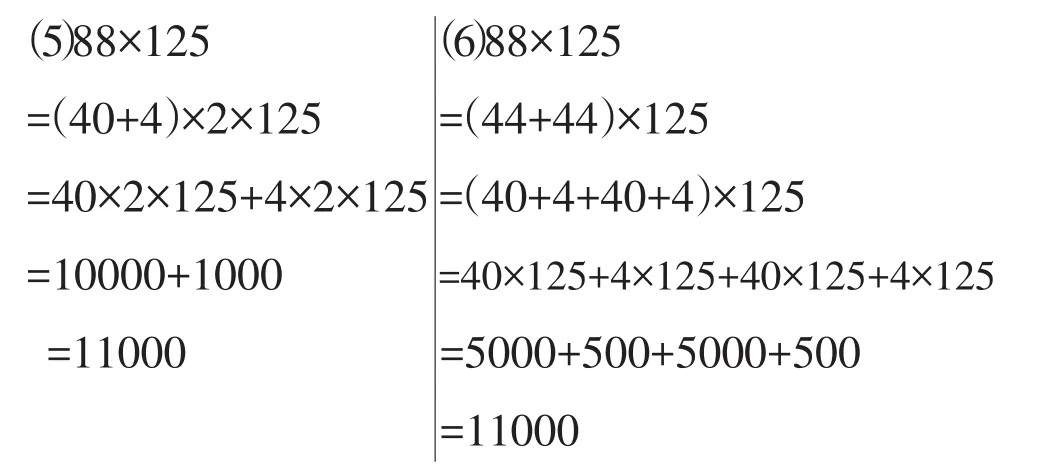
【教学思考】

本节课旨在引导学生将运算定律的学习与简便计算应用及解决现实问题相联系，灵活选择算法，注重解决策略多样化，突破思维定势，提高学生分析、判断、推理的能力，从而增强学生运用简便方法的择优意识。在课堂教学中，教师应结合学生的实际情况开展活动，注重多样化策略展示，更要关注学生对各种方法之间的比较和沟通。

1.在多样化的策略下，欣赏接纳学生的个性方法。

当黑板上呈现这几种方法时，我甚感意外！学生从哪里冒出如此多的方法？通过举手示意，大多数学生认为，第一种和第四种方法比较简便。有一名学生却表示自己的方法（第三种）也简便，众生表示不解。这名学生说：“我们知道8×125=1000，而40是8的5倍，40×125当然就是5000了；48是8的6倍，48×125当然是6000了。40×125=5000，48×125=6000。这样算并不麻烦，我觉得比较简便。”

此时大家恍然大悟，我在一旁也深感惭愧！如果不倾听这名学生的想法，怎么能读懂他的个性解法呢？很明显，这名学生灵活运用了之前所学的“积的变化规律”这个旧的数学知识，不正说明他对这部分知识已经融会贯通了吗？什么是最简便的方法？我认为，简便方法不一定是统一的方法，简便是因人而异的。这让我想起美国著名教育心理学家奥苏伯尔曾说过的一句话：“假如让我把全部教育心理学仅仅归纳为一条原理的话，那么，我将一言以蔽之：影响学习的唯一最重要的因素就是学生已经知道了什么，要深明这一点，并应据此进行教学。”可见，每种方法都是建立在学生已有知识经验之上的。我们在教学时要做好充分的预设，并在课堂进程中时刻关注学生的反应，倾听他们的心声。

2.在多样化的策略下，对比感受学生的繁琐方法。

第二种方法明显是受72×125的影响，这名学生尝试运用了减法，结果感觉不够简便。对于此做法，我表示理解，因为之前在做72×125的时候，这名学生一定是深切体会到了把72分解成（80-8）的简便效果，但做88×125时没有认真观察数的特点，导致盲目使用，却没有达到简算的效果。为此，我引导大家分析比较前后两道题的不同，为什么前面那道题可以分解成减法，后面这道题用减法却不简便呢？通过这样的反思活动，使学生对不同情况灵活选择不同的方法有了深刻的认识，如果教师采取简单否定的做法，势必失去一次探究学习的机会。

选用第五种方法的学生，采用了更多的分解步骤，出现了40×250和4×250的情况，所以在后面的计算中也是比较简便的。询问这样做的原因，学生说：“一方面是对数特点的观察，一方面是逐步尝试计算。”对于这种方法，并没有到此结束，因为我从这名学生的做题步骤中发现了新的教学契机。这道题如果用这种方法做，第二步是很容易出错的，于是我想到了过去的典型错题教学，本道题部分学生很可能会采用40×2+4×125的形式。因此，我提出问题：第二步正确吗？为什么？能不能证明一下？有的学生很快明白了：因为结果正确，每一步推导也没有问题，所以肯定正确。也有学生说，我们可以把括号后面的两个数相乘就是（40+4）×250，这不就是乘法分配律的基本形式吗？那么，这个算式能不能写成40×2+4×125的形式呢？通过热烈讨论，学生对问题越辩越明。

最后一种方法分解得更细。除了带有学生明显的个性化特点外，我还引导学生观察这种方法是对乘法分配律的拓展运用，刚才所学的括号里都是两个数，那么四个数也同样适用，这样的引导使学生对乘法分配律的理解更深了一步。

总之，在解决问题策略的多样化教学中，当学生出现个性化解法时，教师要尊重学生的想法，简便与否不能一概而论；当学生出现繁琐的方法时，教师除了从简便的角度分析外，还要让学生深刻地理解运算定律的本质特征。运算律是运算的主要性质，反映了运算的规律性。学习运算律不仅是为了计算简便，更要深化学生对数与运算意义的理解，培养数学学习的能力。