大跨度自锚式悬索桥钢-STC组合桥面箱形加劲梁抗风性能试验研究

(1.湖南省交通规划勘察设计院有限公司， 湖南 长沙，410219； 2.株洲市城市建设发展集团有限公司， 湖南 株洲 412007)

0 引言

与地锚式悬索桥相比，自锚式悬索桥无需大体量的锚碇，具有造型美观、线型优美等优点，在城市桥梁建设中得到广泛应用。基于自锚式悬索桥受力特点，混凝土加劲梁的跨度非常有限，大跨度自锚式悬索桥常采用钢箱加劲梁。

为解决正交异性钢桥面因刚度较小带来的疲劳开裂和铺装易损等难题，株洲枫溪大桥创造性地将STC超高性能轻型组合桥面应用于自锚式悬索桥，极大地降低了钢桥面的开裂风险，延长了桥面铺装使用寿命。

超高性能轻型组合桥面加劲梁在大跨度自锚式悬索桥体系中具有很好的应用前景。同时，自锚式悬索桥随着跨度增大，结构动力效应显著，对大跨度自锚式悬索桥STC组合桥面加劲梁进行抗风性能研究具有重要意义[1-8]。

本文以株洲枫溪大桥为工程背景，采用有限元计算和节段模型试验相结合的方法，研究大跨度自锚式悬索桥宽幅STC组合桥面钢箱加劲梁抗风性能，为类似桥梁的设计研究提供参考。

1 工程背景

株洲枫溪大桥是株洲市的重要跨湘江通道，主桥跨径布置为(3×45+300+3×45)m双塔单跨自锚式悬索桥，矢跨比为1/5，如图1所示。加劲梁采用钢—STC组合桥面闭口钢箱梁，桥面宽度32 m，中心梁高3.5 m，横向吊点中心距为25.5 m，见图2。

图1 株洲枫溪大桥总体布置(单位： cm)Figure 1 General layout of zhuzhou fengxi suspension bridge(Unit： cm)

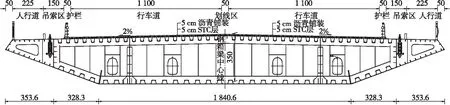
图2 STC组合桥面加劲梁横断面(单位： mm)Figure 2 Cross section of stiffening girder with STC composite deck(Unit： mm)

2 自锚式悬索桥动力特性分析

2.1 结构动力分析模型

为了进行风荷载作用下的结构抖振响应分析、节段模型测振风洞试验研究，桥梁结构动力特性分析是研究桥梁振动问题的基础。

株洲枫溪大桥成桥状态下的结构动力特性分析采用离散结构的有限元方法，基于大型通用有限元软件ANSYS平台，其总体坐标系以顺桥向为X轴，以横桥向为Z轴，以竖向为Y轴，建立全桥动力分析模型，如图3所示。

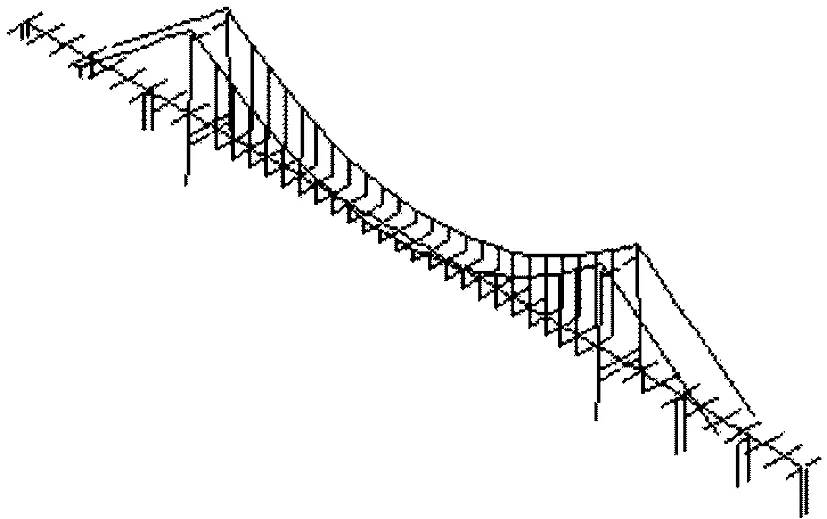
图3 全桥动力分析模型Figure 3 Dynamic model of suspension bridge

枫溪大桥的整体结构是由加劲梁、桥塔、主缆和吊杆等主要构件组成，其主要构件截面特性参数如表1所示。

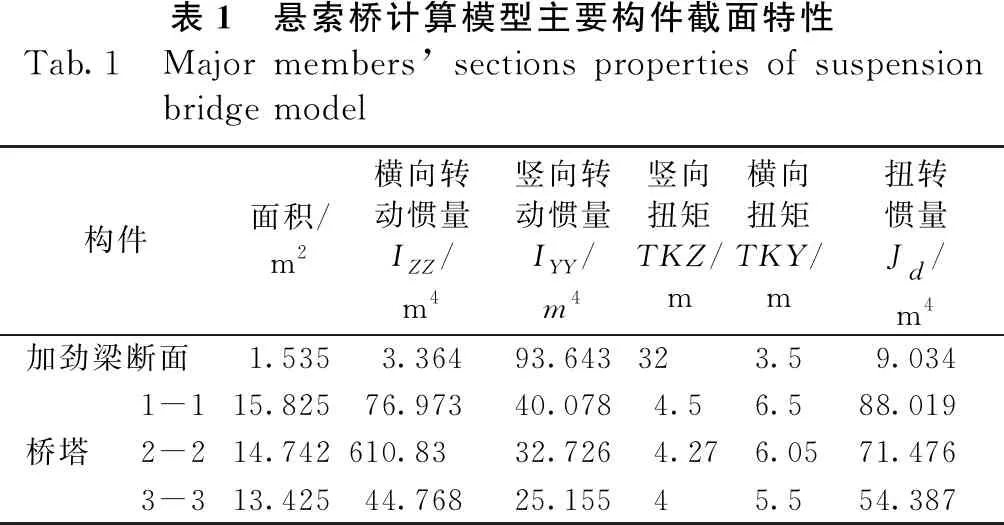
表1 悬索桥计算模型主要构件截面特性Tab.1 Major members’ sections properties of suspension bridge model构件面积/m2横向转动惯量IZZ/m4竖向转动惯量IYY/m4竖向扭矩TKZ/m横向扭矩TKY/m扭转惯量Jd/m4加劲梁断面 1.5353.36493.64332 3.59.0341-115.82576.97340.078 4.5 6.588.019桥塔2-214.742610.8332.726 4.276.0571.4763-313.42544.76825.155 4 5.554.387

2.2 结构动力特性计算结果

基于自锚式悬索桥ANSYS动力仿真模型，进行结构动力特性分析，结构振型主要表现为侧弯、竖弯和扭转，动力特性分析结果如表2所示。

表2 结构动力特性分析结果Tab.2 Dynamic analysis results of structure振型描述频率/Hz等效质量/(t·m-1)等效质量惯矩/(t·m2·m-1)一阶正对称侧弯0.577 71.80 E+02一阶反对称侧弯0.956 93.69E+01一阶正对称竖弯0.447 52.81E+01一阶反对称竖弯0.533 32.73E+01一阶正对称扭转1.295 42.24E+03一阶反对称扭转2.098 72.13E+03

3 加劲梁节段模型测振风洞试验研究

3.1 设计风速参数

根据桥位地理位置和地形特征，确定枫溪悬索桥的设计风速参数如表3所示：

3.2 加劲梁风洞测振试验节段模型

根据节段模型相似性原理，制作1/70缩尺模型，节段模型为薄壁箱形结构，是由铝合金框架与纤维木板板覆面组成，桥面栏杆、检修轨道和风嘴等均选用ABS材料雕刻而成。加劲梁节段模型采用洞外支架悬挂，整个节段模型测振悬挂系统如图4所示。

表3 枫溪悬索桥设计风速参数表Tab.3 Design wind speed parameters of fengxi suspension bridge(m·s-1)基本风速风剖面系数成桥设计基准风速成桥颤振检验风速静力扭转发散检验风速25.6B类,α=0.1630.345.460.6

图4 加劲梁风洞测振试验节段模型Figure 4 Segmental model of stiffening girder for wind tunnel tests

在均匀流场中针对施工图设计阶段加劲梁原始断面进行了节段模型颤振风洞试验，包括-3°、0°和+3°的3种风攻角，共3个试验工况，测试内容包括颤振临界风速、阻尼-风速曲线及气动导数识别。

3.3 颤振试验结果

通过直接试验法测定的结构颤振临界风速、气动阻尼随风速增加的变化规律及气动导数随折减风速的变化。

3.3.1阻尼-风速曲线

通过对加劲梁断面形式进行颤振风洞试验，其实测的成桥状扭转阻尼比随风速增加的变化规律如图5所示。

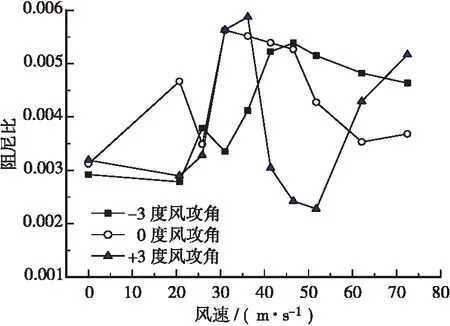
图5 加劲梁系统扭转阻尼比-风速曲线Figure 5 Torsional damping ratio of stiffening girder changing with wind speed

3.3.2气动导数识别

针对钢 — STC超高性能轻型组合桥面加劲梁成桥状态断面采用了弯扭耦合振动形式，运用自由振动气动导数识别方法进行气动导数测定试验，结果如图6所示。

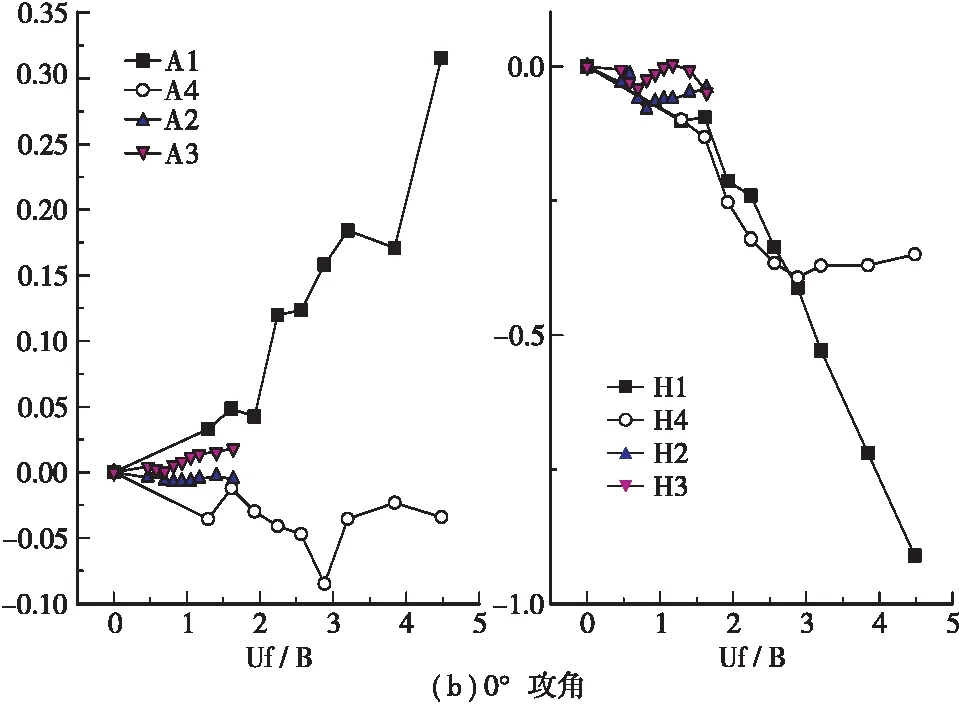
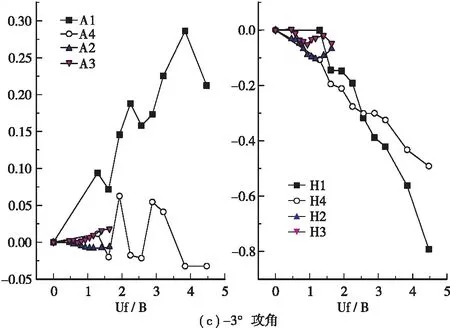
图6 折减风速 — 气动导数曲线

3.3.3颤振临界风速

不同工况下的桥梁结构颤振临界风速风洞试验实测结果显示：加劲梁竖弯阻尼比为0.34%，扭转阻尼比为0.329%，-3°、0°和+3°的3种风攻角工况下，+3°风攻角工况颤振风速最小，临界风速为172.5 m/s，远高于检验风速45.4 m/s。

3.4 涡振试验结果(见表4)

根据《公路桥梁抗风设计规范》中的规定，株洲枫溪大桥竖弯、扭转涡激共振振幅允许值分别为：扭转涡激共振振幅允许值为:[θa]=4.56/Bft=0.011°；竖弯涡激共振振幅允许值为: [ha]=0.04/fb=0.089 4 m。

风洞试验结果显示：成桥状态下的原始断面在+3°攻角下出现11.1～16.7 m/s与22.7～33.4 m/s 两个竖弯涡振区，以及风速大于47.4 m/s的扭转涡振区(已经超过颤振检验风速，不做考虑)，其中在第二个竖弯涡振区，其峰值振幅0.188 m超过规范所允许的振幅值。

表4 涡振振幅峰值及其风速表Tab.4 Peak amplitudes and wind speeds of vortex induced vibration涡振试验工况断面形式风攻角涡振形式共振风速/(m·s-1)峰值振幅WZ-1(原型断面)WZ-2(无检修轨道)WZ-3(检修轨道移至斜腹板)WZ-4(检修轨道移至斜腹板并增设过江管道)3°无//0°//+3°竖弯11.1～16.70.050 m竖弯22.7～33.40.188 m+3°无//3°无//0°无//+3°竖弯10～12.30.026 m扭转21.3～28.40.048°3°竖弯8.5～10.70.037 m+3°竖弯8.9～11.80.053 m扭转25.2～28.30.031°

为了使该桥施工图设计方案涡激共振性能满足规范要求，需要对原始断面进行改进。首先去除检修轨道，对无检修轨道断面进行涡振试验，以确定涡振的产生是否是由于检修轨道的布置引起的。风洞试验结果表明，无检修轨道断面在+3°攻角下未发生涡振，这就说明布置在下甲板上的检修轨道是引起该桥竖弯涡激共振的主要原因。

将检修轨道移至斜腹板中央(改进断面)，并进行+3°、0°以及-3°攻角下的涡振试验。风洞试验结果显示改进断面仅在+3°攻角下发生竖弯涡振(10～12.3 m/s)和扭转涡振(21.3～28.4 m/s)，但是峰值振幅较小，均未超出规范允许值(0.110°及0.089 4 m)。

对于增设过江管道的断面(检修轨道移至斜腹板下缘)，风洞试验结果表明，在-3°攻角下发生竖弯涡振(8.5～10.7 m/s )，但是峰值振幅(0.037 m)较小，未超出规范允许值(0.089 m)；在+3°攻角下发生竖弯涡振(8.9～11.8 m/s)和扭转涡振(25.2～28.3 m/s)，但是峰值振幅较小，均未超出规范允许值(0.110°及0.089 4 m)。

4 节段模型测力风洞试验研究

4.1 加劲梁风洞测力试验节段模型

根据节段模型相似性原理，制作1/70缩尺模型，测力试验除气动外形相似外要求节段模型刚性尽可能大，但对质量和质量惯矩没有相似性要求。加劲梁测力节段模型竖直安装在测力天平上，以用于测力风洞试验。如图7所示。

图7 加劲梁风洞测力试验节段模型Figure 7 Segmental model of stiffening girder for wind tunnel tests

4.2 测力试验结果

定义静力三分力的方向如图8所示，加劲梁断面风轴坐标系下三分力系数定义如下：

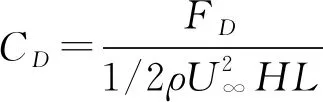
(2)

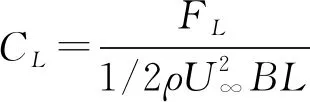
(3)

(4)

加劲梁断面体轴坐标系下三分力系数定义如下：

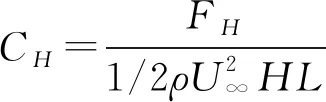
(2)

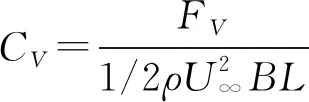
(3)

(4)

式中：U∞为试验风速；空气密度ρ=1.225 kg/m3；L为测力节段模型长度；其中阻力系数以加劲梁高度H为参考长度；升力系数、气动俯仰扭矩系数均以加劲梁断面宽度B为参考长度。

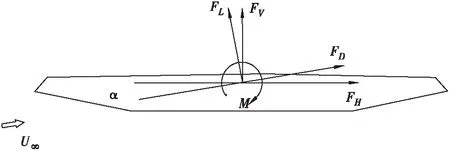
图8 加劲梁静力三分力方向示意Figure 8 Coordinate sketch-map of static forces of stiffening girder

成桥状态加劲梁断面在风轴和体轴状态下的静力三分力系数随攻角的变化趋势如图9所示。

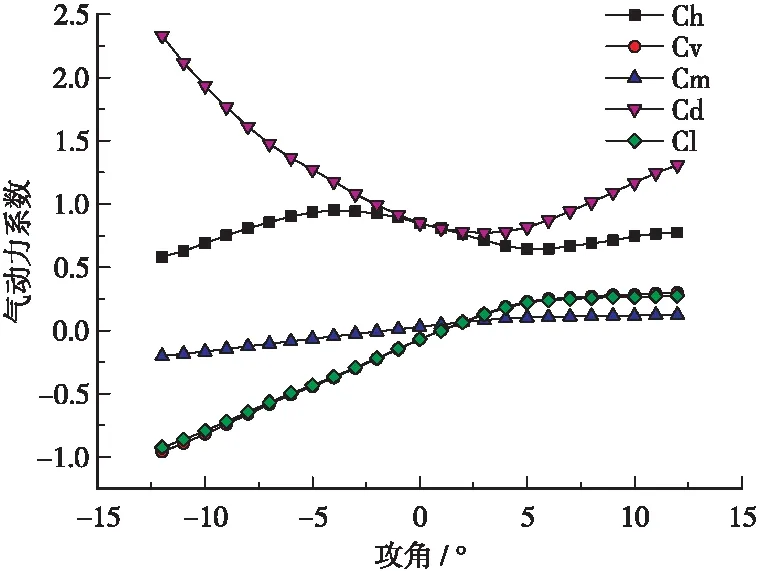
图9 静力三分力系数随攻角的变化Figure 9 Aerodynamic coefficients change with angle of attack

5 结论

以株洲枫溪大桥为工程背景，采用有限元分析、节段模型试验相结合的方法，研究大跨度自锚式悬索桥钢—STC组合桥面宽幅箱形加劲梁抗风性能。并得到以下结论：

枫溪大桥设计基准风速为Vd=30.3 m/s、成桥状态颤振检验风速为[Vcr]=45.4 m/s、二维静风稳定性检验风速为Vtd=60.6 m/s。

结构一阶竖弯、侧弯和扭转频率分别为0.447 5、0.577 7和1.295 4 Hz。

钢—STC组合桥面宽幅箱形加劲梁结构在-3°、0°及+3°的3种风攻角下颤振临界风速均远高于桥位处检验风速，表明设计方案满足颤振稳定性要求，且有较大富余度。

成桥状态下的原型断面在+3°攻角下出现了11.1～16.7 m/s与22.7～33.4 m/s两个竖弯涡振区，其中在第二个竖弯涡振区，其峰值振幅0.188m超过规范所允许的振幅值。通过对截面进行局部优化，竖弯涡振和扭转涡振的峰值振幅均大幅降低，均在规范允许值以内。

节段模型测力风洞试验基于风攻角为-12° 至12° 范围内变化，研究了加劲梁断面的静力三分力系数的变化规律。

本文基于枫溪大桥加劲梁风洞试验及静动力特性分析，研究了大跨度自锚式悬索桥的钢—STC组合桥面箱形加劲梁的抗风性能，为类似桥梁的设计研究提供依据和参考。