基于集对联系数的围岩稳定性组合评价模型研究
(1.中交第三公路工程局有限公司,北京 100102; 2.湖南大学 土木工程学院,湖南 长沙 410082;3.湖南湖大建设监理有限公司,湖南 长沙 410082)
0 引言
随着我国交通运输行业的不断发展,公路和铁路的路网规模不断扩大、路网结构日趋完善[1]。我国西部地区的地形以高原和山地为主,在公路和铁路的建设中,道路越岭成为山区道路施工的最佳选择,隧道在线路中所占的比重越来越大[2-3]。在隧道施工中,为了经济合理地进行工程规划选址、岩体加固设计和安全施工,需要预先对围岩稳定性进行评定[4]。准确可靠地确定围岩稳定性等级,具有重要工程价值和意义。
围岩的稳定性受多种因素影响与控制,且各因素具有多样性、可变性、不确定性等特点,使得围岩的稳定性评价成为一个复杂的不确定性问题[5]。对于围岩的稳定性评价,学者们提出了定性与定量相结合的多指标评价方法,如可拓方法[6]、云模型法[7]、BQ法[8]、投影寻踪法[9]、粗糙集法[10]和灰色理论法[11]等。目前关于围岩稳定性评价的研究不断深入,考虑的因素也愈来愈全面,但由于这一复杂问题的不确定性,每一种评价方法都有着不足。如可拓法在计算关联度时以区间中值为最优,忽略了重要的约束条件,使得评价结果与实际情况存在差异;灰色理论法在样本数据波动较大时,其评价结果容易产生偏差。单一的评价方法大多利用部分信息片段从特定角度对围岩稳定性进行分析与评价,导致不同方法获取的结果存在差异,使决策者难以抉择。
集对分析理论是一种新的处理不确定系统问题的理论[12-13]。其将确定性和不确定性作为一个系统进行分析,为围岩稳定性评价问题提供了新的思路和途径。同时,组合评价的思想可综合单项评价模型的优势,提高评价结果的可靠性[14]。因此,本文基于组合评价的思想,利用集对分析理论表达单项评价模型间信息的差异性,并基于正态分布理论合理确定集对关系准则,进而利用集对联系数定量分析单项评价模型间的集对关系,并基于集对联系数确定组合权重系数,获得围岩稳定性组合评价模型,为围岩稳定性评价问题提供新的解决思路。
1 基于集对联系数的围岩稳定性组合评价模型
1.1 基本原理
组合评价模型是基于联系度对单项评价模型信息的可靠性与有效性进行定量分析,进而对单项评价模型的信息进行有效组合,提高组合评价的可靠性和有效性。基于集对联系数的围岩稳定性组合评价,首先选取合理的单项评价模型对围岩稳定性进行评价,并基于评价结果将单项评价模型两两构建为集对;其次基于构建的集对信息,利用正态分布理论确定集对关系划分准则;再次基于集对关系准则,获得两两评价模型间的联系度,并基于联系度计算各单项评价模型的组合权重系数;最后应用线性组合加权方法获得围岩稳定性评价分数,确定围岩稳定性等级。
1.2 集对分析理论
集对分析理论是中国学者赵克勤提出的一种确定和不确定系统分析理论[15]。该理论通过集对同异反关系刻画确定和不确定系统中的对立统一关系,并以联系度μ来描述系统中确定和不确定性的相互联系。对由集对的N个样本展开集对关系分析,若其中处于同一性关系的样本数为S,处于差异性关系的样本数为F,处于对立性关系的样本数为P,则联系度则可表达为下式:
(1)
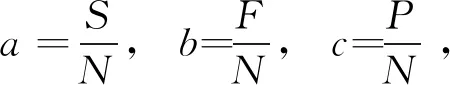
μ=a+bi+cj
(2)
其中,a,b和c分别为集对的同一度、差异度和对立度,且a+b+c=1。
1.3 集对关系准则的确定
集对关系准则是集对分析的核心和关键。传统的主观隶属度法无法应用于集对关系准则未知的不确定性问题。三等分法常被用来解决集对关系准则未知的不确定性问题[12],但该方法仅依据样本数据的最大值和最小值对数据分布区间进行三等分,而对样本数据的分布特征及包含的信息缺乏考虑,进而未能合理地体现数据内部包含的集对关系。基于上述考虑,本文从集对关系的分布特征入手,基于样本的整体信息对集对关系准则进行划分。
考虑到单项评价模型信息的确定性与不确定性,各单项评价模型的评价结果一般相差不大,较为接近,其集对关系可认为是差异性关系;较少数的评价结果会显著地差异很小或很大,这两种情况下的集对关系可认为分别是同一性关系和对立性关系。因此,集对关系准则可描述如下:若评价结果间的差异处于区间(α,β)中,则认为此时的集对关系为差异性;若评价结果间的差异处于区间[0,α],则认为此时的集对关系为同一性;若评价结果间的差异处于区间[β, +∞),则认为此时的集对关系为对立性。
由于单项评价模型的有效性,不同模型对某一样本评价结果之间的差异值往往在一个范围内上下波动,差异值极小或极大的情况较少。因此,不同评价模型间的差异值呈现出正态分布的特征。本文考虑利用正态分布理论对集对关系的阈值进行确定,进而基于正态分布参数获得集对关系准则。
1991年,《国务院关于大力发展职业技术教育的决定》中提出“产教结合、工学结合”,在国家顶层路径导向上,拉开了职业院校与企业合作办学的实践序幕。1996年至2014年,先后有《中华人民共和国职业教育法》,以及教育部《关于以就业为导向深化高等职业教育改革的若干意见》《关于实施国家示范性高等职业院校建设计划加快高等职业教育改革与发展的意见》,国务院《关于加快发展现代职业教育的决定》等政策法规出台,均就职业学校校企合作提出明确要求。国家顶层设计确定了职业教育发展方向及定位:走校企合作之路。
在正态分布的假设检验中,样本的差异值大多集中在区间(μ-σ,μ+σ)内。同时根据上述分析,较多的差异值处于差异性关系,即落在差异性关系区间(α,β)内。鉴于正态分布参数的内涵与集对关系阈值相吻合,选用正态分布参数(μ-σ,μ+σ)作为差异性关系区间(α,β)。相应地,较少的差异值会落在区间(-∞,μ-σ]和[μ+σ, +∞)内,同时较少的差异值会处于同一性关系和差异性关系,因此,选用正态分布参数(-∞,μ-σ]作为同一性关系区间,选用[μ+σ, +∞)作为对立性关系区间。因此,基于正态分布理论的集对关系准则可用图1和式(3)表示。

图1 基于正态分布的集对关系准则Figure 1 Set pair relationship criterion based on normal distribution
{p≤μ-σ同一性关系
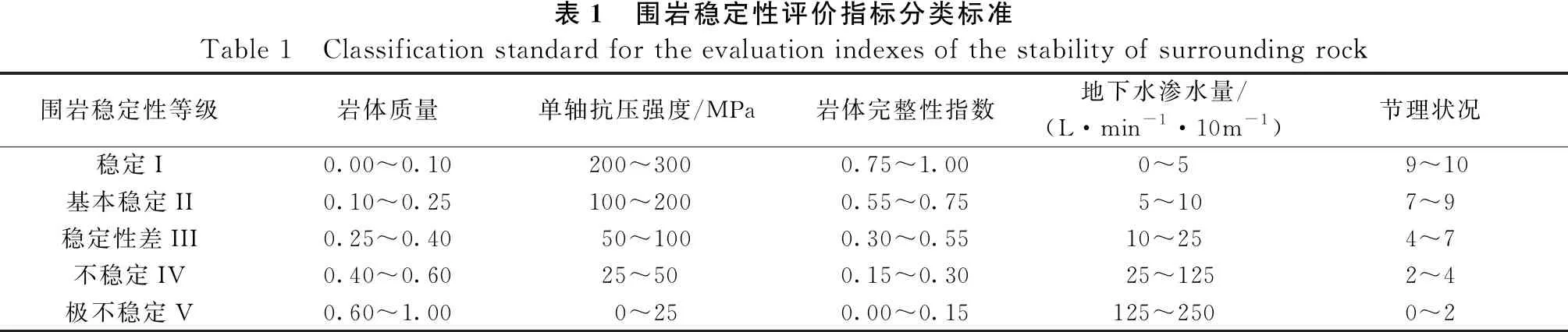
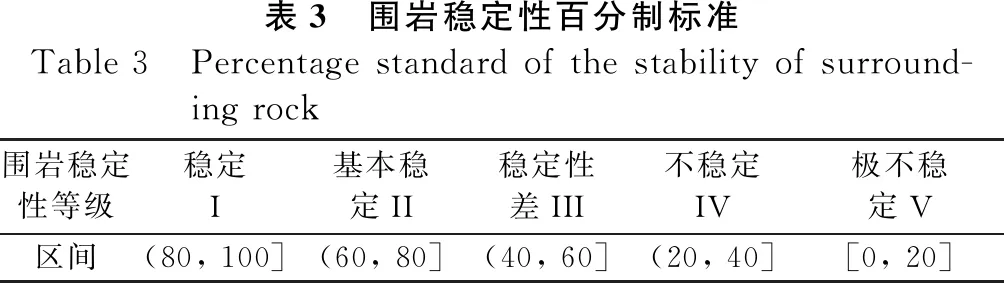
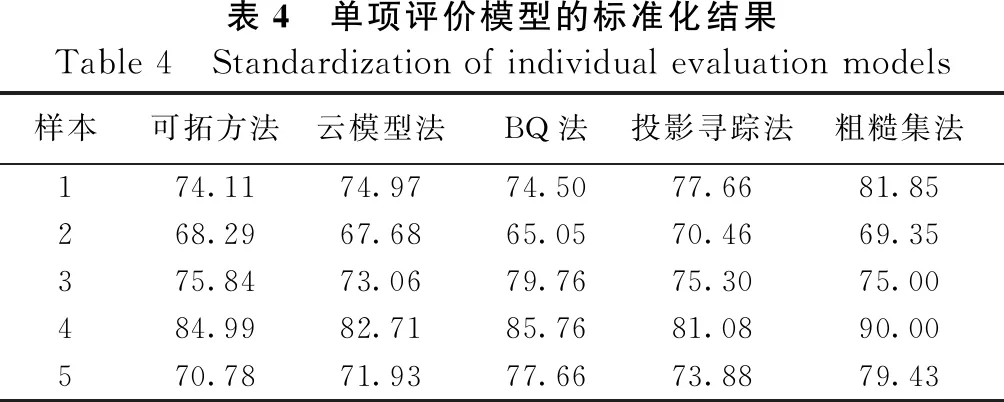
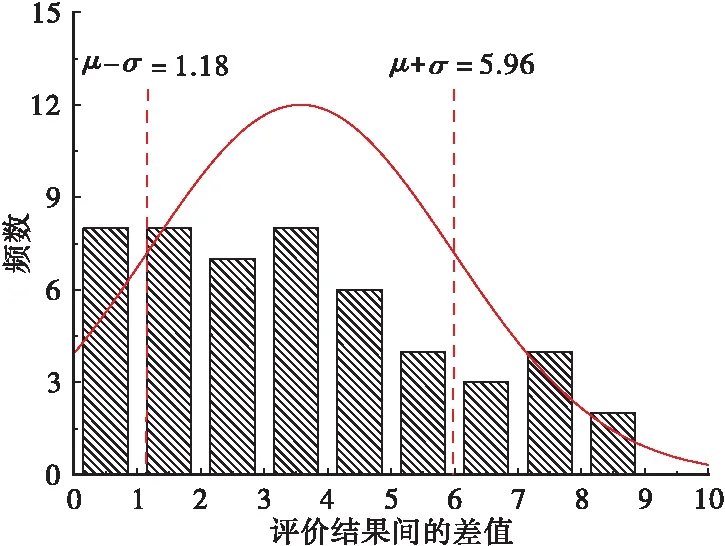
μ-σ p≥μ+σ对立性关系 (3) 组合评价模型的核心是权重系数的确定。集对联系数定量刻画了评价模型间信息的确定性与不确定性关系,表达了各评价模型的可靠性与有效性,因此,可利用集对联系数确定权重系数。 首先,基于图1和式(3)所示的集对关系准则,对单项评价模型间的集对关系进行定量分析,分别统计集对关系为同一性、差异性以及对立性的样本个数[式(1)],获得单项评价模型间的联系度[式(4)];然后,对联系度进行归一化处理,获得组合权重系数[式(5)];最终,采用线性加权法对各评价方法结果进行组合,获得组合评价结果[式(6)]。相应的权重及组合评价模型如式(4)至式(6)所示。 (4) (5) (6) 在围岩稳定性评价问题中,作为评价的独立因素一般有围岩质量、围岩完整性以及地下水情况等[4-6]。本文选取了岩体质量、单轴抗压强度、岩体完整性指数、地下水渗水量以及节理状况等5个指标作为围岩稳定性评价指标[9]。依据相关规范,将围岩稳定性等级分为稳定I、基本稳定II、稳定性差III、不稳定IV和极不稳定V等5个等级,如表1所示。 在应用组合评价模型对围岩稳定性进行评价前,应先选取合理的单项评价模型。已有的研究结果表明,可拓方法、云模型法、BQ法、投影寻踪法和粗糙集法在围岩稳定性评定中可获得合理可靠的结果[6-10]。因此,本文选取这5种评价模型作为单项评价模型,各评价模型的计算过程见文献[6-10]。 表1 围岩稳定性评价指标分类标准Table 1 Classification standard for the evaluation indexes of the stability of surrounding rock 围岩稳定性等级岩体质量单轴抗压强度/MPa岩体完整性指数地下水渗水量/(L·min-1·10m-1)节理状况稳定I0.00~0.10200~300 0.75~1.000~5 9~10基本稳定II0.10~0.25100~200 0.55~0.75 5~107~9稳定性差III0.25~0.4050~1000.30~0.5510~254~7不稳定IV0.40~0.6025~50 0.15~0.30 25~1252~4极不稳定V0.60~1.000~250.00~0.15125~2500~2 表2 围岩样本评价指标的实测值Table 2 Measured values of the evaluation indexes of sur-rounding rock samples样本岩体质量单轴抗压强度/MPa岩体完整性指数地下水渗水量/L·min-1·10 m-1 节理状况10.12185.50.896820.27176.40.808730.08158.20.946740.04201.10.975950.24181.90.9298 由于各评价模型的评价结果会以不同形式给出,为使不同评价方法的结果具有可比性,在将单项评价模型构建为集对前,应首先对评价结果进行标准化。同时,为便于工程应用以及方便比较,标准化后的结果采用工程界应用最为广泛和简便的定量转换方法—百分制评分方法。鉴于围岩稳定性划分为5个等级,围岩稳定性百分制标准也均等地划分为5个等级,如表3所示。 表3 围岩稳定性百分制标准Table 3 Percentage standard of the stability of surround-ing rock围岩稳定性等级稳定I基本稳定II稳定性差III不稳定IV极不稳定V区间(80, 100](60, 80](40, 60](20, 40][0, 20] 以可拓方法为例,对标准化的过程予以说明。对于样本1,可拓方法获得的样本关于I~V等级的关联度x1″分别为-0.137、0.161、-0.456、-0.693和-0.789。由于评价结果未在实数范围内,故首先进行数据预处理,如式(7)所示,使之处于实数范围内。 (7) 式中:x1″为样本1评价结果(关联度),x1′为实数化后的评价结果。再将实数化后的评价结果进行标准化,如式(8)所示。 (8) 式中:pt为围岩稳定性百分制标准中各等级区间的中值,当等级t=1、2、3、4和5,pt依次取90、70、50、30和10。按照上述标准化方法,可获得各单项评价模型的标准化结果,如表4所示。 表4 单项评价模型的标准化结果Table 4 Standardization of individual evaluation models样本可拓方法云模型法BQ法投影寻踪法粗糙集法174.1174.9774.5077.6681.85268.2967.6865.0570.4669.35375.8473.0679.7675.3075.00484.9982.7185.7681.0890.00570.7871.9377.6673.8879.43 对于各单项评价模型,基于评价结果的差值(绝对值)构建集对。统计差值的分布情况,并利用正态分布理论确定集对关系准则。基于正态分布理论,获得该分布的平均值μ=3.57,标准差σ=2.39。根据上述关于集对关系阈值的规定,采用μ-σ,μ+σ作为集对关系划分阈值,即α=1.18,β=5.96。单项评价模型间的差值分布情况及集对关系阈值如图2所示。各单项评价模型间的集对关系准则可确定为式(9)。 图2 差值的分布情况及集对关系阈值Figure 2 Distribution of difference and set pair relationship threshold {x≤1.18 同一性关系 1.18 x≥5.96 对立性关系 (9) 基于集对关系准则式(9),对单项评价模型间的集对关系进行定量分析。统计各集对中集对关系为同一性、差异性和对立性的样本个数,基于式(1)和式(2)获得单项评价模型间的联系度,如表5所示。 表5 单项评价模型间的联系度Table 5 Connection degree between individual evaluation models可拓方法云模型法BQ法投影寻踪法粗糙集法可拓方法1+0i+0j25+35i+0j25+25i+15j15+45i+0j25+15i+25j模型法25+35i+0j1+0i+0j15+35i+15j05+55i+05j05+25i+35jBQ法25+25i+15j15+35i+15j1+0i+0j05+55i+05j05+45i+15j投影寻踪法15+45i+0j05+55i+05j05+55i+05j1+0i+0j25+25i+15j粗糙集法25+15i+25j05+25i+35j05+45i+15j25+25i+15j1+0i+0j 在差异度系数i取0.5,对立度系数j取-1的条件下,上述联系度可转化为联系数。利用式(4)和式(5)将联系数进行归一化,获得组合评价的权重系数,如表6所示。最后,利用式(6)将单项评价模型的评价结果进行线性加权组合,获得在百分制区间内的围岩稳定性评价结果。本文组合模型的围岩稳定性评价结果及与其它模型结果的对比见表7。 表6 组合权重系数Table 6 Combined weight coefficient可拓方法云模型法BQ法投影寻踪法粗糙集法0.230.180.220.250.12 表7 评价结果及与其它模型结果的对比Table 7 Evaluation results and comparison with other models样本本文模型BQ法投影寻踪法[9]粗糙集法[10]176.20(II)IIIII268.16(II)IIIIII375.96(II)IIIIII484.41(I)III574.33(II)IIIIII 由表7可知,本文的评价结果与常用评价模型的结果相吻合,表明基于集对联系数的组合评价模型应用于围岩稳定性分析是可行的。对于粗糙集法,无论是规范化后的评分还是最终的等级评定,该模型都与其它模型存在明显差异,表明该模型包含的结果信息与其它模型存在明显差异。因此,其联系数最小,该方法的有效性与可靠性最低,其组合权重系数也最小。而对于其它单项评价模型,无论是规范化后的评分还是最终的等级评定,结果间的差异都较小,表明各评价模型间的信息基本一致,其权重系数也较为接近。本文模型通过集对联系数,定量地分析了各评价模型间信息的差异,并基于联系数的内涵表达组合权重系数,合理有效地对单项评价模型的信息进行组合,达到降低评价风险、综合单项评价模型优点的效果。 此外,本文基于样本集对关系的分布特征以及整体信息,利用正态分布理论确定集对关系阈值,构建了基于正态分布理论的集对关系准则确定方法。该方法能够深入挖掘各评价模型所包含信息的确定性与不确定性,有效地提高了集对关系识别的精度,进而更加合理地对单项评价模型间的集对关系进行分析,优化单项评价模型间的信息组合。 围岩稳定性问题涉及交叉和交融等不确定性因素,应用单一的分析方法往往结果不太理想。本文基于组合评价的思想,利用集对联系数构建了围岩稳定性组合评价模型。研究结果如下: a.基于集对联系数的组合评价模型应用于围岩稳定性分析是可行的。该组合评价方法将围岩稳定性评价问题作为一个确定与不确定的系统进行数值处理,通过联系数分析围岩稳定性评价的确定性与不确定性,并定量刻画单项评价模型的有效性与可靠性。基于联系数确定组合权重系数,对单项评价模型的信息和优点进行融合,克服了单项评价模型信息片面性的缺陷,获得了可靠性更高的评价结果。 b.以正态分布理论为基础的集对关系准则确定方法基于样本集对关系的分布特征以及整体信息对集对关系进行划分,避免了三分法主观确定集对关系的缺陷和不足,提高了集对关系的识别精度,为集对关系准则未知的不确定性问题提供了新的处理思路,也为集对联系数理论的推广应用提供了理论支撑。1.4 权重的确定及组合评价模型
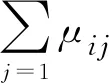
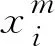
2 实例应用
2.1 围岩稳定性评价指标及分类标准
2.2 工程应用分析




3 结语

