三角翼滚转运动的首次穿越分析
彭如月, 焦萌倩, 黄文韬, 蒋贵荣
(1.桂林电子科技大学 数学与计算科学学院,广西 桂林 541004; 2.广西师范大学 数学与统计学院,广西 桂林 541004)
在航空领域,三角翼作为当今较受欢迎的飞行器,它的滚转运动问题值得深入研究。三角翼飞行器在飞行过程中会遇到很多不确定因素,导致飞行事故的发生。因此,在研究三角翼的滚转运动时,考虑随机激励很有必要。当三角翼飞行器受随机外激或随机参激时,会使系统响应在相空间中发生随机变化,此时需要考虑系统的可靠性。 在随机动力学中可靠性研究是一个难点[1],学者们在这方面做了大量研究。文献[2-3]研究了基于拟可积Hamilton系统和不拟可积Hamilton系统的铁路桥梁动力可靠度。朱位秋等[4]利用随机平均法研究了随机激励系统的首次穿越与可靠性问题。文献[5]通过建立可靠性函数的后向Kolmgolov方程和广义Pontryagin方程,分析了色噪声激励下的非线性阻尼动力系统的首次穿越问题。
三角翼飞行器有较悠久的研究历史,三角翼因其优良的气动特性在军用飞机和无人机上获得了广泛的应用[6]。李乐奇[7]设计了一种双回路的无人机滚转运动的PID控制器,但未考虑外界干扰的影响。牛中国等[8]从来流条件和激励参数分析了DBD (dielectric barrier discharge)等离子体激励对三角翼流动控制效果的影响规律,并对三角翼前缘涡控制的发展进行总结展望。大攻角情况下,机翼摇滚是一种典型多自由度耦合运动,它的滚转运动是最主要的自由度[9]。文献[10]采用旋转升力和动态失速2种不同的方法,研究了扑翼产生的非定常气动力降阶模型。文献[11]利用多种方法分析了三角翼滚转运动的随机响应。
目前,涉及到三角翼滚转运动的文献大部分是利用多方面耦合的方法研究摇滚气动特性问题,且得到的大多是一个数值结果,对于三角翼滚转运动的首次穿越问题的研究较少;利用数学方法研究三角翼单自由度滚转运动问题的文献也较少。因三角翼外部干扰的文献也不多,关于三角翼滚转运动首次穿越的研究就更少。
鉴于此,研究高斯白噪声激励下三角翼飞行器滚转运动的稳定性和可靠性问题。建立三角翼滚转运动的随机动力学模型,利用最大Lyapunov指数分析稳定性,最后加入一个PID控制律,利用滚转角比例参数和滚转角速度比例参数来减少期望滚装角与实际滚转角的误差。理论分析与数值模拟相结合,对三角翼滚转运动的首次穿越时间距进行了比较。
1 三角翼随机动力学模型
考虑三角翼飞行器单自由度滚转运动,讨论滚转角随时间变化的定量和定性规律,其滚转运动方程[12]为
(1)

系统(1)未考虑随机因素,然而实际因素对飞机在飞行过程中的影响很大,所以在系统(1)中加入高斯白噪声,模型如下:

(2)
设滚转力矩系数为
(3)
将式(3)代入式(2),得
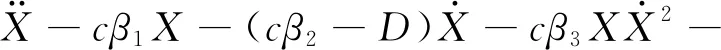
(4)
令ω2=-cβ1,α1=-(cβ2-D),α2=-cβ3,α3=-cβ4,α4=-cβ5,则整理式(4)可得三角翼飞行器在高斯白噪声激励下的滚转运动动力学模型:

(5)
其中:W(t)为具有谱密度K的高斯白噪声;ω2和αi(i=1,2,3,4)均为系统参数。

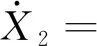
其中,X1、X2分别为三角翼滚转运动的滚转角和滚转角速度。
在系统(5)的无阻尼自由振动方程中,其势能和总能量分别为:
由于能量过程是一个慢变过程,可近似为马尔科夫扩散过程,系统(5)可依概率收敛到一维扩散过程,由伊藤方程支配[4]:
dλ=m(λ)dt+σ(λ)dB(t),
其中:B(t)为标准Wiener过程;m(λ)、σ(λ)分别为伊藤随机过程的漂移和扩散系数。
运用能量包线随机平均法[4],可计算得到系统(5)的漂移和扩散系数:
(6)
(7)
为求解系统(5)的随机响应过程的转移概率密度函数,给出系统(5)相应的FPK(fokker-planck-kolmogorov方程[4]):
(8)
对于随机动力系统(5),其稳定性主要由平稳解决定,将式(6)、(7)代入式(8),得到系统(5)的平稳概率密度p(λ),即平稳解:
其中C为任意常数。
由于系统存在非平凡平稳概率密度,可以考虑系统的样本渐近稳定性。
定义1[4]若对每个ε1,ε2>0,存在δ(ε1,ε2,t0)>0,使得
成立,且对每个ε>0,存在δ(ε,t0)>0,使得
只要‖x0‖≤δ,由于ε任意小,则称样本渐近稳定。
非线性随机动力学系统(5)的样本渐近稳定性只取决于最大Lyapunov指数rmax,因此,系统(5)的渐近稳定的充要条件为rmax<0。
2 随机稳定性
最大Lyapunov指数是判断非线性随机动力学系统的渐近稳定性的重要参数。通过计算线性化系统的最大Lyapunov指数讨论非线性随机系统(5)平凡解的局部稳定性。
定理1当α1<πK/2ω时,系统(5)的线性伊藤随机微分方程的平凡解(0,0)渐近不稳定,此时三角翼飞行器在随机扰动的影响下会出现失稳现象。
证明系统(5)存在一个平凡解O(0,0),伊藤随机微分方程在零点处存在唯一平凡解。将漂移系数与扩散系数在λ=0处线性化,得到线性化的伊藤随机微分方程:

令Y=lnλ,利用伊藤微分规则可得到Y的伊藤方程:
(9)
解得式(9)的形式解为
所以可得:
故最大Lyapunov指数为

当r>0,即α1<πK/2ω时,系统(5)的线性伊藤随机微分方程的平凡解渐近不稳定。定理证毕。
3 受控系统的稳定性
对于飞行器而言,其飞行控制系统在实际中至关重要,它的优劣程度将直接影响飞机安全飞行的各项性能。所以在系统(5)的基础上,借鉴经典的PID控制[7],在系统(5)中加入控制律e,利用滚转角比例参数和滚转角速度比例参数来减少期望滚装角与实际滚转角的误差,得到以下受控的动力学方程:

(10)

定理2当KD<α1-πK/2γ时,随机系统(10)线性化伊藤随机微分方程的平凡解是局部渐近稳定的。
证明用能量包线随机平均法可得相应支配的伊藤随机微分方程:
dλ=me(λ)dt+σe(λ)dB(t),
其中:
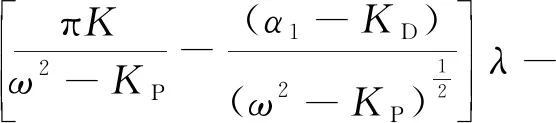
加入控制律后,系统(10)的线性化伊藤随机微分方程为
可解得系统(10)在平衡点处线性化的最大Lyapunov指数为
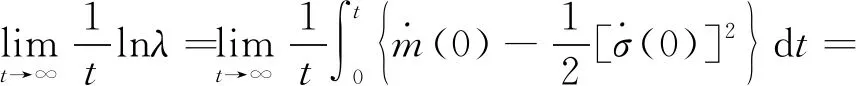
(11)
根据式(11),KD<α1-πK/2γ时,有re<0,从而受控系统(10)线性化伊藤随机微分方程的平凡解是局部渐近稳定的。定理证毕。
4 受控系统的首次穿越
系统可靠性问题主要考虑可靠性函数Re(t,t0,λ0),它为给定初始状态λ0∈[λl,λc)的条件下,在t时刻系统处于λl≤Λ(t)<λc的概率,

其中:p(λ,t|λ0,t0)为过程λ(t)在超越右边界(λc)之前的转移概率密度;λl为能量过程λ(t)的左边界。
令τ=t-t0,则可靠性函数Re(t,t0,λ0)可记为Re(τ,λ0),转移概率密度p(λ,t|λ0,t0)满足后向科尔莫戈罗夫方程(backward Kolmogorov,简称BK)[4]:
(12)
其中me(λ0)、σe(λ0)为受控的漂移和扩散系数。
考虑到求解可靠性函数比较困难,而求解首次穿越时间的统计量较为简单,当λ(t0)=λ0时,能量过程λ(t)首次到达临界值λc(λ0<λc),称其为发生了首次穿越[4]。
首次穿越时间的均值与可靠性函数之间的关系[4]为

(13)
根据式(12)、(13),可得广义Pontryagin(GP)方程[4]:
(14)
根据式(14),解得加入控制律后的首次穿越时间的n+1阶距:

其中:
因首次穿越时间非负,不同阶的距的统计量具有相同的趋势,因此,一阶矩是最重要的[4]。当n=0时,加入控制律后首次穿越时间距为
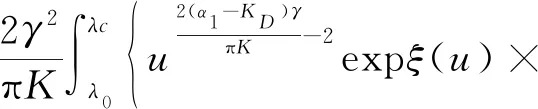
(15)
5 数值模拟
在系统(5)中,取K=0.2,ω2=0.16,α2=1.2,α3=0.8,α4=0.49。根据定理1,取α1=0.6πK/2ω=0.471 2。 取初始点为(3,2)。图1为变量x的时间序列图的样本。从图1可看出,系统(5)的零解不是随机稳定的。
根据定理2所示,取Kp=0.15,KD<0.7(α1-πK/2γ)。从图1可看出,系统(10)中的x趋向于0,从而随机系统(10)线性化伊藤随机微分方程的平凡解是局部渐近稳定的。

图1 变量x的时间序列
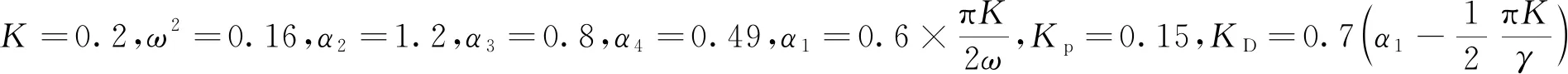
当参数K=0.2,ω2=0.01,α1=0.047,α2=1.2,α3=0.8,α4=0.19,Kp=-0.15,KD=1.8,λ0=1,λc=10时,图2 为系统(5)和(10)的首次穿越时间距。
在系统(5)和(10)中,取ω2=0.01,α1=0.047,α2=1.2,α3=0.8,α4=0.19,Kp=-0.15,KD=1.8,λ0=1,λc=10,关于K的首次穿越时间距如图2所示。当K=0.34时,系统(5)的首次穿越时间距约为152,施加控制后,系统(10)的首次穿越时间距明显增大,约为351,从而提高了系统的可靠性。
W(t)为具有谱密度为K的高斯白噪声,K∈[0.3,0.6]。从图2可看出,当K=0.42时,系统(5)、(10)的首次穿越时间距约为41和82,随着噪声强度的增加,系统的首次穿越时间距均减少。
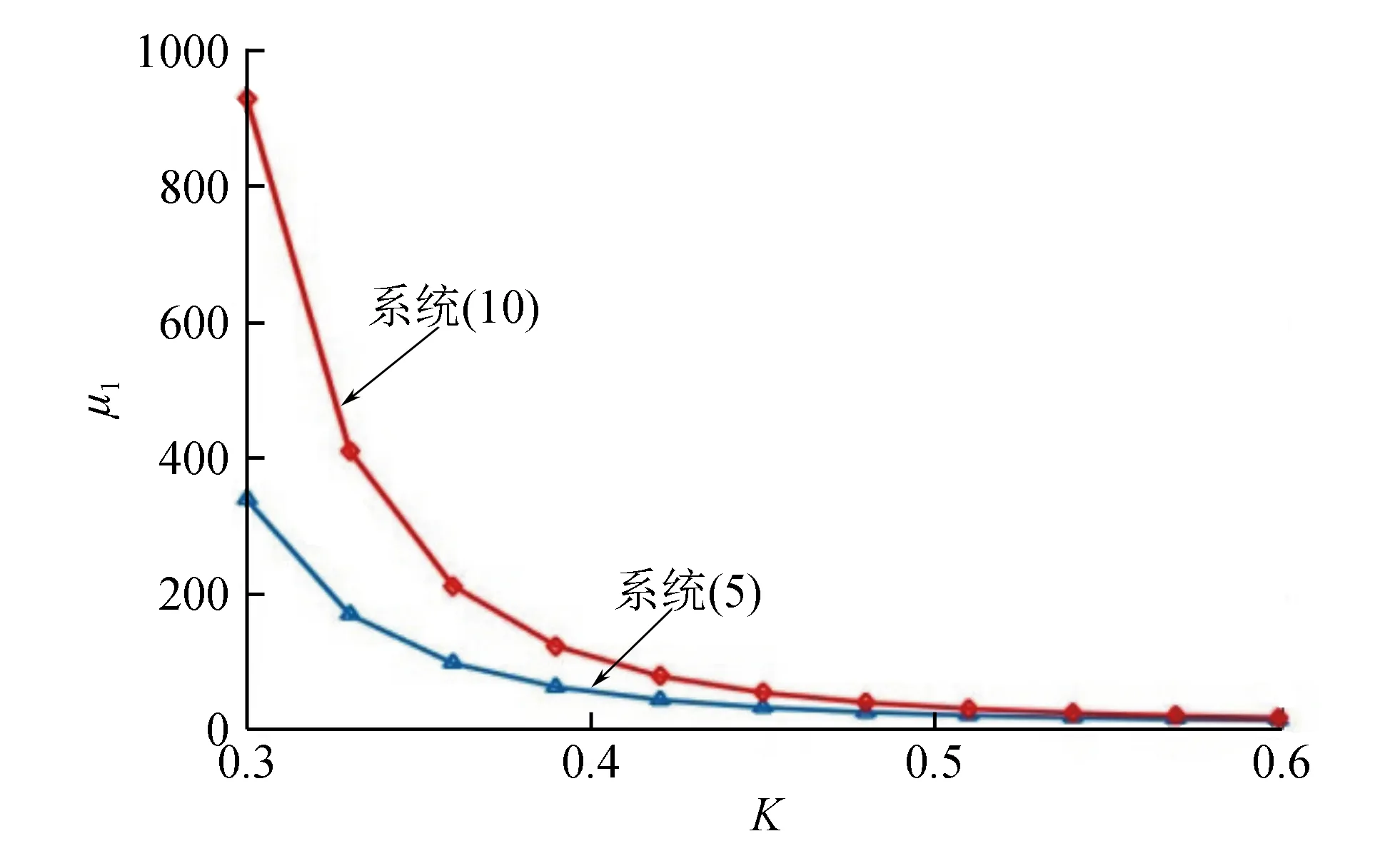
图2 首次穿越时间距
6 结束语
针对三角翼飞行器在随机激励影响下滚转运动的稳定性,研究了三角翼飞行器滚转运动在高斯白噪声影响下发生的首次穿越问题。利用能量包线随机平均法将非线性随机函数表示为一维扩散过程,通过最大Lyapunov指数分析系统的局部稳定性,建立可靠性函数和首次穿越时间的距所满足的BK方程,计算出首次穿越时间距。通过加入一个控制律,对比了不加控制与加入控制的时间距,并对结果进行数值模拟。结果表明,加入的控制律能使平均首次穿越时间距明显增大,有良好的控制效果。本研究的不足之处是考虑的噪声激励是高斯白噪声,自然界的随机干扰很复杂,对于其他噪声还需进一步研究。

