基于核函数NPSSB模型的HY-2A卫星雷达高度计海况偏差研究

张洁，田杰，王兆徽

（1.国家海洋环境预报中心，北京100081；2.国家海洋局空间海洋遥感与应用研究重点实验室，北京100081）

1 引言

海况偏差（Sea State Bias，SSB）是由于海表面存在波浪引起的，会造成实际的高度计测距大于真实距离的一种误差[1]，因此海况偏差为负值。它是卫星雷达高度计测高的主要误差源之一。按照误差产生的原因，海况偏差由：电磁偏差、偏斜偏差和跟踪偏差这3种误差构成[2]。其中电磁偏差是由于在雷达脉冲与海面相互作用时，海表面波浪的波谷比波峰更多地反射了脉冲，会导致平均反射面低于真实平均海面[3]，关于这一点，Gaspar等[4]曾做过相应的研究，发现平均反射面和真实平均海面之间的高度差为-1%～-4%的有效波高（Significant Wave Height，SWH）；另外两种偏差：偏斜偏差和跟踪偏差，都是由仪器产生的误差[5]。星上跟踪器的作用是确定高度计返回脉冲波形上升沿半功率点的位置，在计算中假设海面的高度概率密度函数成高斯分布，由于实际波形是非高斯型或是偏斜的，所以产生偏斜和跟踪偏差，与SWH成正比[6]。高度计海况偏差计算模型从参数模型发展到非参数模型（Nonparametric，NP）[7-9]。参数模型有BM系列模型（Bias Model）、基于波浪发展的SSB校正模型和基于波浪统计特征参数经验模型。在参数的选择方面从单一考虑有效波高和风速到把伪波龄、后向散射截面、涌浪高度、波浪陡度和波周期等因子加入模型。BM海况偏差参数模型主要有4种：BM1、BM2[4]、BM3[10]和 BM4[4]。广泛采用的 SSB经验校正模型是BM4模型[11]。

根据众多理论研究以及塔基、风洞等现场的测量[8、12-14]表明：高度计测高误差ΔR和SSB相关的影响因素不仅有风速、有效波高，还与不同成长阶段的波浪相关，这样就有了基于波浪不同发展阶段的SSB校正模型，即FG模型[8]。该校正模型中，波浪的成长程度用经验参数伪波龄（Pseudo Wave Age）来描述[15-16]。FG模型表达式如下：

式中：Hswh是有效波高，ξ是伪波龄，ξm是全球平均伪波龄参数，其值约为2.3[9]，伪波龄的计算公式如下：

式中：U为风速。参数经验模型都是引入SSB真值进行修正的模型，而SSB真值的获取来自现场试验，如利用激光和陆地上塔基雷达试验，操作起来比较困难。

SSB参数模型中的海况偏差系数为常值，对于这一点，许多学者都存在异议。Cheney等[16]对Geosat数据按照不同纬度区间进行研究，发现海况偏差系数具有0.2%～1.8%的变化，Zlotnicki等[17]也进行了类似的研究，结果海况偏差系数变化范围为2.3%～2.9%。Witter等[18]对Geosat海况偏差进行分析，发现海况偏差与纬度存在从40°S的2.2%到10°S～40°S的3.2%这样的关系，同时指出由纬度导致的海况偏差的变化，这一现象的实质是不同纬度区域存在不同有效波高，而海况偏差系数的不同则是由有效波高造成的。Labroue等[19]研究也指出有效波高相对于的海况偏差系数的有较高的影响。因此许多学者展开了SSB非参数校正模型的研究。Witter等[20]首先提出针对风速影响的海况偏差系数非参数校正模型，和参数模型具有具体的函数形式不同，非参数校正模型没有具体的函数形式，模型结果就是风速与海况偏差系数为一一对应，按照风速的大小，即可得到相对应的海况偏差系数。Chelton[1]认为海况偏差系数应是非参数的，并且是风速与有效波高的函数，而非预先假定一个经验模型，再用卫星测高数据进行拟合。Chelton[3]和Rodriguez等[20]都对海况偏差非参数模型进行了研究。

“海洋二号”（HY-2A）卫星是我国发射的首颗海洋动力环境卫星，星上搭载了主、被动微波遥感器（高度计、辐射计和散射计），具有高精度测轨、定轨和全天候、全天时、全球探测能力[21-22]。卫星的精确重复周期分为寿命前期和寿命后期，寿命前为14 d，寿命后期为168 d。卫星寿命前期的轨道高度为971 km，卫星寿命后期的轨道高度是973 km。对全球海面高度的观测是HY-2A卫星的一项重要工作内容。通过HY-2A长时间的数据积累，使得其成为全球卫星测高体系的重要补充[23]。

由于卫星定轨技术的提高，海况偏差取代轨道误差成为高度计最大的误差源[24]。Labroue等[19]和Picot等[25]经过研究证明NPSSB模型是目前精度最高的海况校正模型。Jason-2采用的是NPSSB模型计算海况误差，HY-2A卫星高度计采用的是BM4模型计算海况偏差，利用HY-2卫星和Jason-2卫星海况偏差在交叉点处的数据分析，表明HY-2A卫星海况偏差在交叉点处的方差是Jason-2的两倍，且存在-2.5 cm的平均差值[11]。

机器学习是现代智能技术中重要的一个方面，研究从观测样本出发去分析对象，进行预测。其中径向基函数（Radial Basis Function，RBF），就是某种沿径向对称的标量函数[26]。通常定义为空间中任一点x到某一中心xc之间欧氏距离的单调函数，其作用往往是局部的，即当x远离xc时函数取值很小，可以表示点x和点xc的关系。最常用的径向基函数是高斯核函数。

本文拟研究实现基于长时间序列的HY-2A卫星高度计数据，包括风速、有效波高和海面高度差值，基于高斯核函数的NPSSB模型算法，将计算结果和SSB参数模型中具有代表性的BM3和BM4模型的海况偏差校正数据进行对比，探究BM3、BM4模型与高斯核函数NPSSB模型之间的差异。

2 方法

本文的研究思路如图1所示，首先收集HY-2A卫星高度计二级产品数据，在经过判断完整性、解码、读取观测数据后，对观测数据进行筛选，包括标识筛选和阈值筛选。对获取到的质量较好的数据进行除SSB外误差校正，误差项包括：干湿大气延迟、电离层延迟、海洋潮汐、海洋负荷潮、地球固体潮、逆大气压校正和极潮。以3 d为时间窗口，利用求升轨和降轨交叉点的方法，分别计算每个周期的交叉点处海面高度不符值、风速和有效波高矩阵。结合核函数NPSSB的相关算法，模拟SSB的值，与BM3和BM4模型结果进行对比。

3 数据采集及处理

3.1 数据采集

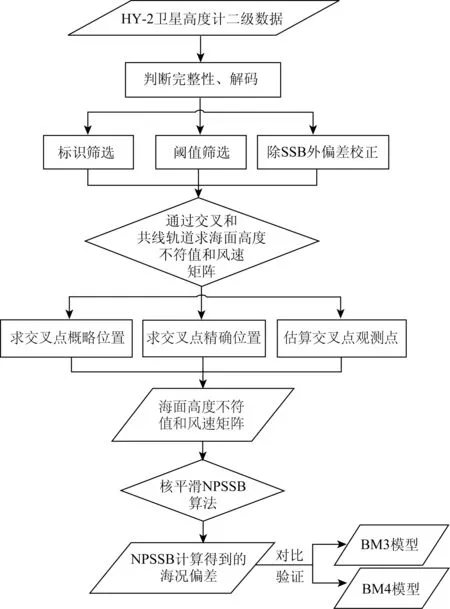
图1 流程图

本研究所需高度计数据由国家卫星海洋应用中心提供的HY-2A卫星高度计二级数据产品。二级数据为已经过海陆标识和质量控制后的产品数据。采集了 0012、0013、0018、0019、0020、0021、0022、0023、0025、0026、0032、0044、0045和0046共14个周期数据。

3.2 数据筛选

采集数据后首先判断数据的完整性、对数据进行解码，然后为了保证高度计卫星观测数据的质量，需要对其进行筛选剔除异常，包括标识筛选和阈值筛选。标识筛选是根据高度计数据集中测量参量标记值直接剔除不合格数据；阈值筛选则是指当测量参数的值在阈值范围之外时，说明该点数据异常，予以剔除。标识筛选选项和阈值筛选项见表1、2。

2014年以前的合格处方百分比均低于30%，其中2013年、2014年的百分比均低于20%。惠州市根除Hp处方合格率基本上逐年上升，由2010年的24.14%上升到2016年的51.41%。见表2、图3。

经过上述数据采集和处理后，统计数据量，发现采集14个周期的原始数据量都在9×105左右，经过标识筛选和阈值筛选的后数据量在4×105左右，具体数据量变化见图2。

3.3 交叉点处海面高度不符值、风速和有效波高矩阵的获取

对筛选后得到的数据进行除SSB外的偏差订正，包括：干湿大气延迟、电离层延迟、海洋潮汐、海洋负荷潮、地球固体潮、逆大气压校正和极潮。

表1 数据标识筛选标准

表2 数据阈值筛选标准

图2 14个周期原始数据量和筛选后数据量对比

式中：SSH′是除SSB外的偏差订正后的海面高度，altitude是卫星相对参考面高度，range_ku是卫星相对瞬时海面高度，ε代表上述所列各项误差。

利用HY-2A卫星高度计数据的time_day和time要素，以3 d为时间窗口，对每个周期的数据，计算3 d内高度计升、降轨交叉点，最后将一个周期的所有交叉点汇总。

为了避免计算量过大，利用下述判定条件判断两个轨道是否有可能交叉。HY-2A卫星高度计数据中，以pass序号的奇、偶性可以辨别该轨道的升降属性：奇数的轨道为升轨，偶数的是降轨。在确定轨道的升降属性后，通过以下4个条件判断升降轨是否有可能形成交叉点：①升轨弧段开始经度大于降轨弧段结束经度；②升轨弧段结束经度小于降轨弧段开始经度；③升轨弧段开始纬度小于降轨弧段开始纬度；④升轨弧段结束纬度大于降轨弧段结束纬度。

对可能交叉的的升降轨弧段求交叉点的方法如图3所示。首先找到升降轨弧段上距离最近的4个点A1、A2、D1和D2（A表示升轨，D表示降轨），并分别在所在的弧段两端各扩展5个点，以扩展后的一共24个点进行多项式拟合，求交点，交点处即为交叉点位置。交叉点处的位置信息：经纬和纬度，由这24个点拟合的两条曲线求交点得到。交叉点风速包括：升轨风速和降轨风速，由升轨和降轨的12个点插值得到。同理可以得到升轨有效波高、降轨有效波高、升轨 SSH′（SSH′A）和降轨 SSH′（SSH′D）。交叉点处的海面高度不符值Δhs按照式（4）计算得到。

图3 求交叉点示意图（A表示升轨，D表示降轨）

得到[交叉点经度，交叉点纬度，升轨风速，降轨风速，升轨有效波高，降轨有效波高，Δhs]数据集后，需要再进行数据筛选，去掉异常值点。理论上我们认为3 d时间内，海面高度变化值应小于20 cm，即：Δhs≤0.2 m，并且高纬度地区误差较大，所以当Δhs＞0.2 m或者交叉点在高纬度地区（＞60°N或者60°S）时，判定其为异常值点，需要去除。以0012周期为例，通过上述方法，得到的交叉点如图4所示。

3.4 核函数NPSSB算法

在前人的研究基础上，我们能够得知海况偏差可以看做是自变量为风速和有效波高的函数，因此本研究在获取大量海面高度不符值、风速、有效波高数据样本的基础上，结合高斯核函数探寻海况偏差和二者之间的机制，结果并不是给出类似BMSSB参数模型的函数表达式，而是利用数据样本之间的规律，在设定自变量的情况下，给出因变量的值。完整推导公式在下文阐述。

图4 0012周期（4445—4447 d）交叉点分布（蓝色为交叉点、红色为观测点）

回归方程为：

式中：权重值an必须满足以下条件：

结合海面高度不符值矩阵(yi,x1i,x2i)，得到SSB表达式为：

下标1和2对应相同地理位置不同的观测时间，i表示第i个观测，假设 φ(x1i)已知，把x用x1i替换，求解φ(x1i)：

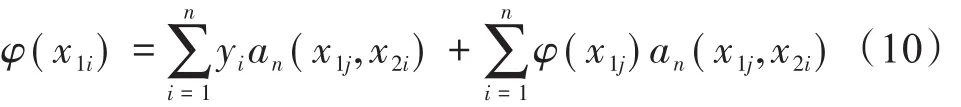
写成矩阵形式：

I是n×n的单位矩阵，A的大小也为n×n，其矩阵元素 aij=an(x1j,x2i)，φ1=[φ(x11),…,φ(x1n)]T，y=[y1,…,yn]T。此矩阵为奇异矩阵，必须给定φ1一个确定值φ0，则上式可重写为：

求解得到SSB：

A是权重矩阵，权重大小由xi和x之间的距离比例因子来确定，其表达式为：

式中：K是核函数，hn是带宽向量，n表示带宽取决于观测样本，在核函数NPSSB模型中，选择对称的高斯核函数：

带宽的计算公式为：

式中：可以是风速U或者有效波高hswh，σx是x的标准差，C是取决于核函数的常数，对于高斯核函数，其值为1.06。n是数据集的大小。φ0的确定采用下述方法：在符合SSB取值范围内，任意给定φ0一个值，计算得到φ(U,SWH)的值，最终SSB的值为φ(U ,SWH)的值减去φ0。x11的确定是通过两步得到：第一步计算一个周期内所有交叉点的U、SWH值的平均值，第二步在交叉点的集合中找到距离U、SWH平均值最近的点，定义为x11。

4 分析验证

在求取上述14个周期的[交叉点经度，交叉点纬度，升轨风速，降轨风速，升轨有效波高，降轨有效波高，海面高度不符值]数据集后，分别计算各周期的SSB，求平均SSB的值作为核函数NPSBB模型模拟的结果，通过以下3个方面对模拟的结果进行分析验证。首先分析核函数NPSSB的值与有效波高和风速之间的变化关系；再通过计算核函数NPSSB的标准差评估NP模型对SSB的模拟能力；最后通过与BM3和BM4模型计算的SSB的值进行对比，比较核函数NPSSB模型和BM系列模型模拟的SSB区别。

4.1 核函数NPSSB与有效波高、风速的关系

SSB是有效波高和风速的函数，核函数NPSSB分别随有效波高和风速的变化情况见图5。由图5可知：（1）估计的核函数NPSSB的值都为负数，这与SSB的定义相符；（2）当风速为固定值时，SSB随有效波高的变化呈现反比例函数的关系，随着有效波高的增大，SSB的绝对值也增大；（3）当有效波高为固定值时，SSB随风速的改变呈现近似二次函数的变化趋势，风速小于约9 m/s时，SSB的绝对值随着风速的增加而增加，当风速大于9 m/s时，SSB的绝对值随风速的增加而减小，这与Hevizi实验结果12 m/s[10]有些偏差。

4.2 核函数NPSSB的标准差

通过计算核函数NPSSB的标准差评估NP模型对SSB的模拟能力。标准差由下述公式计算：

式中：N为样本数量。计算得到的标准差如图6所示。

计算核函数NPSSB模型得到的SSB标准差，发现标准差范围在0～12 mm并且呈现从中心向外标准差逐步增大的一个变化趋势。为了探究核函数NPSSB模型得到的SSB标准差分布原因，将实验用到的原始风速和有效波高数据按照（0.5 m/s，0.25 m）为间隔，统计风速和有效波高的分布，如图7所示。对比图6和图7发现，NPSSB的标准差的分布同（风速，有效波高）数据量的分布类似，二者具有一定的关系，在（风速，有效波高）数据量较高的区域，核函数NPSSB的标准差值较小，随着（风速，有效波高）数据量的减少，NPSSB的标准差值逐步增加，这是由NP算法的本质导致的。核函数算法的核心是利用大量样本去学习自变量和因变量之间的关系，通过训练，得到自变量和因变量的变化机制，继而实现对因变量的模拟，样本的数量会影响模拟结果的误差，误差随着样本数量的增加而减小。

图5 NPSSB与有效波高和风速之间的关系

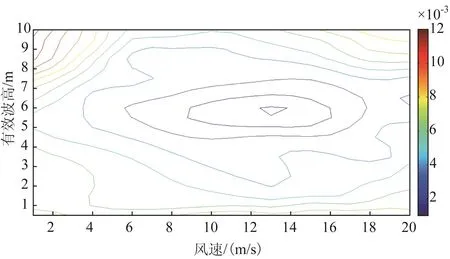
图6 核函数NPSSB模型得到的SSB标准差（单位：m）

图7 风速和有效波高数据量分布

图8 BM模型模拟的SSB值

图9 核函数NPSSB模型与参数模型对比

4.3 核函数NPSSB模型和BM3、BM4模型的对比

BM3模型的计算公式如下：

BM4模型的计算公式如下：

按照核函数NPSSB模型的风速和有效波高范围，计算BM3和BM4模型模拟的SSB值，如下图所示。我们可以发现，BM3模型和BM4模型模拟的SSB的值随风速的变化呈现二次函数的关系，峰值都在12.5 m/s左右。BM3模型SSB随有效波高的变化与NP模型类似，随着有效波高的增加，SSB的绝对值也增加；而BM3模型SSB与有效波高呈现二次函数的关系。

为了比较核函数NPSSB模型和BM系列参数模型的区别，将核函数NPSSB模型与BM3和BM4模型模拟的SSB的值相减，差值见图9。其中图9a为核函数NPSSB模型与BM3模型的差值，图9b为核函数NPSSB模型与BM4模型的差值。我们发现核函数NPSSB模型与BM3、BM4模型差不多都存在0～-0.03 m的差值，这与前人的研究结果相符。核函数NPSSB模型与BM3模型差值的绝对值更大，随着风速和有效波高的增加，差值的绝对值越大。

5 总结和讨论

对14个周期的HY-2A卫星高度计数据进行质量控制，包括标识筛选和阈值筛选，对筛选后得到的数据进行除SSB外的偏差订正，以3 d为时间窗口，得到交叉点处海面高度不符值、风速和有效波高数据集，对数据集进行训练，创建海况偏差核函数非参数模型（NPSSB），并与参数模型中具有代表性的BM3、BM4模型进行对比。

研究表明：（1）核函数NPSSB模型模拟的海况偏差为负值，符合海况偏差的定义，并且能够很好的反映SSB与U、SWH之间的关系：SSB与U呈二次函数关系，SSB与SWH呈反比例函数关系；（2）核函数NPSSB模型对SSB的模拟能力与训练数据集相关，数据量越多，模拟能力越好；（3）核函数NPSSB模型与BM3、BM4模型都存在0～-0.03 m的差值，随着风速和有效波高的增加，差值的绝对值越大。