基于节点分类的k度匿名隐私保护方法
金 叶,丁晓波,龚国强,吕 科
(三峡大学 计算机与信息学院,湖北 宜昌 443002)
0 概述
随着互联网技术的发展,许多移动应用系统和线上交流平台不断出现,形成多种类型的社交网络,如微信、QQ、新浪微博、Facebook、Twitter等[1],这些社交平台拥有上亿的用户并产生海量数据,通过对网络中产生的海量数据分析和研究,可以识别出人们的身份、联系方式等隐私信息,因此针对社交网络数据的保护已经变得至关重要[2]。在发布数据时,如何保证数据具有研究价值和实用性的同时能有效保护数据的隐私信息,也是人们一直关注的问题[3]。在文献[4]提出针对关系型数据的k匿名方法后,数据隐私保护开始衍生出各种各样的匿名方案,针对属性数据有(k,l)[5]、(p,k)[6]等保护方法,而针对具有图结构的数据,采取k度匿名的思想进行匿名隐私保护[7-8]。文献[9]提出针对节点度攻击的k度匿名保护方法,通过增加或者删除边的方式来匿名节点的度。文献[10]通过优化边的选择策略来改进k度匿名,降低了边的修改数目,从而提高数据的实用性。文献[11]通过将节点聚类形成多个“超节点”,每个“超节点”中至少含有k个节点,从而提出簇聚类匿名方法来保护隐私信息。文献[12]提出针对复杂网络的可拓展聚类算法。文献[13]提出通过缩小图中任意两节点间的距离来实现k度匿名保护。
在传统k度匿名保护方法中,匿名算法虽然能快速构建出一个满足k度序列的社交网络图,但是因为对图进行重构,在很大程度上造成了图结构的损坏,节点间的结构关系受到严重破坏,并且该方法在攻击者只拥有节点的度这一先验知识时是具有保护效用的,但当攻击者拥有更强的先验知识时,如节点的一跳邻居结构、节点的社区关系等信息,k度匿名保护方法则无法抵抗这些攻击。本文提出一种改进的k度匿名保护方法,从节点本身出发优化节点的度及图的结构。
1 相关定义
在本文中,社交网络用一个无向无权的图来表示,V表示用户实体,E表示实体间的关系,V={v1,v2,…,vn}是节点的集合,E={(vi,vj)|vi,vj∈V}是边的集合且1≤i,j≤n,deg(vi)或者deg(i)表示图中节点vi的度。本文匿名方法考虑社交网络具有的“小世界”现象[14],对节点进行划分形成多个社区结构,分别对社区内的节点和连接社区的节点采取匿名操作。从整体图来看,实现的是度匿名,但是从节点之间的社区连接来看,也实现了连接关系的匿名,不同的保护策略对不同的节点匿名,达到更好的匿名效果,能有效抵抗社区关系和度等推理攻击手段。
对一个原始的社交网络图数据,本文首先对其进行预处理,将节点划分到不同的社区中,并采用模块度这一概念判断当前节点划分的有效性。
定义1(模块度) 模块度又称模块化度量值,是一种常用的衡量网络社区结构强度的方法[15]。式(1)为模块度的数学表达式:
(1)
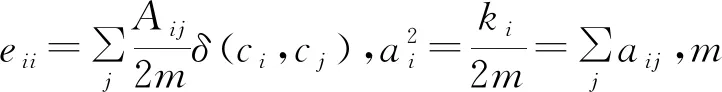
通过模块度的约束,将整个图划分为多个社区子图,每个社区子图包含多个节点,而串联起这些社区子图的节点就是重要的桥梁节点,社区内除去这些桥梁节点,其余的是普通节点。
定义2(边缘节点) 边缘节点又称为桥梁节点,对于划分后的节点,社区中和其他社区存在连接关系的节点称为边缘节点,如属于社区A的节点v,与社区B中的节点u之间有一条边相连,则节点v和u分别是社区A和B中的边缘节点。
边缘节点充当桥的作用,将各个社区串联起来,有着非常重要的影响力和传播力。在现实生活中,充当桥梁作用的用户通常都是与其他用户连接紧密、关系复杂的人,图能够充分体现这一关系,而且社区结构也与 “物以类聚,人以群分”概念相符,相同兴趣爱好的用户聚到一起形成社区,各类用户分布在各个社区中,又由充当桥梁的共同用户互相连接起来,形成复杂的社交网络图[15-16]。对边缘节点的匿名,不仅要考虑节点的度,而且要考虑节点之间的社区关系,攻击者具有的背景知识丰富多样,泄露社区的关系相当于泄露了社区中的节点信息,因此对边缘节点的社区关系匿名比简单的度匿名更加重要。
根据边缘节点的定义可知,多个社区之间通过不同边缘节点连接,一个边缘节点可能与多个社区存在连接关系,统计该边缘节点所连的社区号,则可以得到各个社区的连接关系。
定义3(边缘节点社区序列) 对于一个边缘节点vi,与其相连的社区数为cni,图中所有边缘节点的社区数组成社区序列CN={cn1,cn2,…,cnm} 。
由定义3可知,边缘节点的社区数其实也是边缘节点的度,与度不相同的是这些节点所连的社区之间的关系不同,对这些社区数匿名就相当于对社区关系匿名。
定义4(边缘节点k度匿名) 对于一个边缘节点vi,其连接的社区数为cni,当连接社区个数为cni的边缘节点至少有k个时,满足边缘节点k度匿名。
边缘节点k度匿名引自传统的隐私保护方法k度匿名。此类算法的思想是对于表中的任意一条数据,存在至少k-1条数据在属性上与之相同,则攻击者成功识别该用户属性的概率最大为1/k,本文中的节点匿名也是采用该思想,即隐藏任意节点到k个节点中。
2 基于节点分类的隐私保护方法
2.1 攻击模型
本节对边缘节点攻击模型进行详细阐述,并且针对该攻击模型,提出k度匿名隐私保护模型来抵抗边缘节点攻击。现有的去匿名化方法大多是针对子图结构,先将原始图划分成多个子图,然后对每个子图进行节点去匿名化,对于一些具有明显社区结构的子图,只要运用基本的社区划分算法,就能将节点划分到不同的社区中,之后通过对这些社区中的节点进行k度匿名或者子图匹配,就能快速识别该节点。这种通过图结构关系来去匿名化节点的攻击方法攻击力度非常大,加剧了信息泄露问题。
在图1中,将社交网络图划分为3个社区,由边缘节点1、2、3串联起整个网络图。可以看出,社区B与社区A、社区C都有连接关系,但是社区A和社区C都只与其中一个社区相连,也就是与边缘节点2相连的社区数为2,而边缘节点1和节点3的社区数都为1,即边缘节点的社区数序列为(2,1,1),如果此时攻击者知道某个节点所连的社区数目为2,那么边缘节点2与其所处的社区都可以被识别出来。本文通过更改边缘节点之间的连接关系,间接改变社区之间的关系,实现社区数序列的k匿名,从而对社区和节点进行保护。
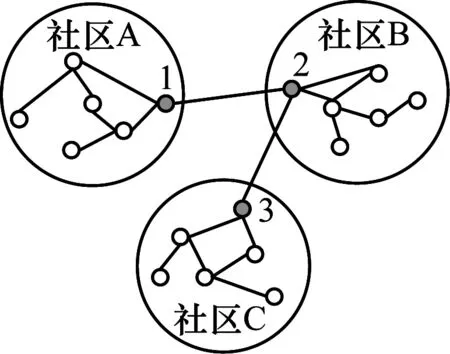
图1 社区关系攻击示意图
2.2 基于节点分类的k度匿名保护模型
对节点进行分类匿名,一类是社区内节点,另一类是连接各个社区的边缘节点。首先对M个社区中的边缘节点进行遍历,统计边缘节点的社区数形成社区数序列,然后判断这个序列是否满足k匿名。如果不满足,则从序列数最小的节点v开始,随机选择节点u=(Cv≠Cu& (u,v)∉E),添加(u,v)这条边,通过不断遍历[17]实现边缘节点的社区数序列k度匿名。对于社区内的节点,首先统计该社区内的度序列,如果度序列满足k度匿名,则该社区不需要进行边的修改操作,当度序列不满足k度匿名时,则在社区内进行边的增加或者删除操作,使得在社区内至少存在k个节点的度相同,实现社区内节点的k度匿名。分别对节点进行匿名后,从整个社区网络图来看,匿名后的图满足k度匿名,并且能够抵抗度攻击和社区聚类攻击。
图2是k度匿名流程。图3是基于节点分类的匿名流程。通过两个流程图可以看出,本文匿名算法无需重构图,这样能保证最大程度地保留原始图结构,并且相比于传统k度匿名算法,节点分类匿名思想可以根据节点的重要性实施不同程度的隐私保护,具有一定的隐私保护伸缩性,比k度匿名更加灵活且符合实际情况。

图2 k度匿名流程
Fig.2 Procedure of implementing k degree anonymity
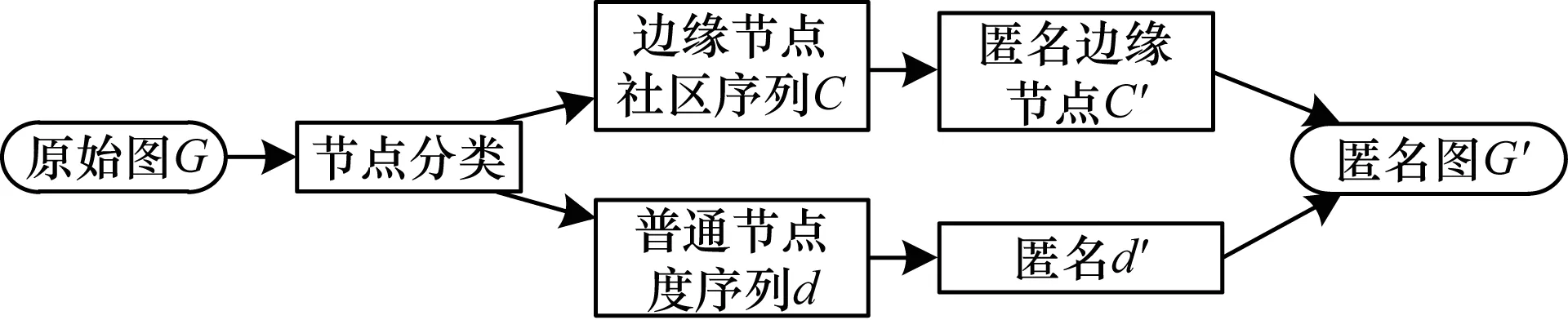
图3 基于节点分类的匿名流程
图4是2度匿名图,其中虚线为增加的边。由此可知,边缘节点1、2、3的原始社区数序列为(2,1,1),而进行边缘节点k匿名之后的度序列为(2,2,2),社区数都为3,是一个3度匿名序列,攻击者就无法以高于1/3的概率来推断出目标社区和社区间关系。在社区内,如A社区,原始的度序列为(1,3,3,3,2,1),度为2的节点只有一个,不满足k度匿名条件,则在社区内进行节点选择及边的增加或者删除操作,最后得到k度匿名序列(2,2,3,3,4,4)是一个2度匿名序列,整个社交网络图实现了2度匿名。
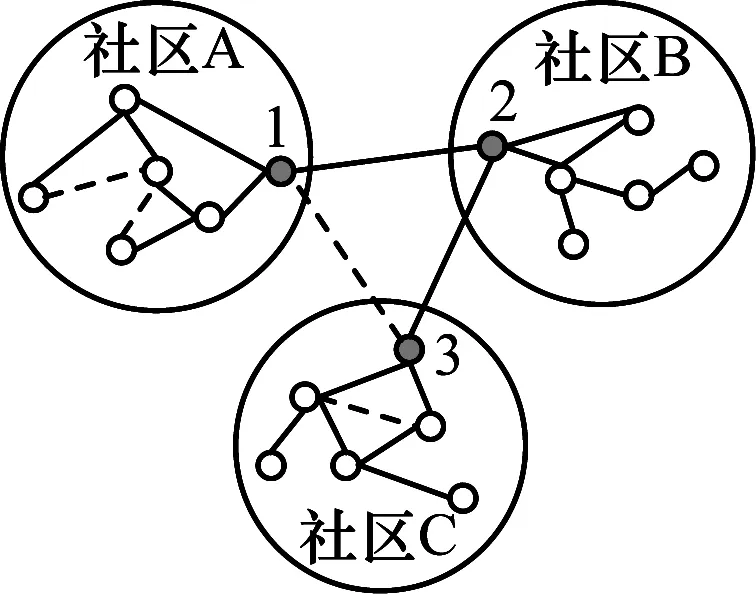
图4 2度匿名示意图
2.3 基于节点分类的匿名算法
一般的隐私保护方案是将整个社交网络看作一个整体,需要不断遍历图中的所有节点,对于节点并没有区分其影响力和传播力。考虑到复杂网络的“小世界”现象,引入社区这一概念,以区分不同节点的影响力,同时对划分后的节点进行分类,重要性不同的节点进行不同程度的匿名保护,并且在匿名过程中无需遍历图中的所有节点,社区内节点的匿名只需搜索查找本社区内其他节点即可,不同社区可同时进行,大幅提高了算法的运行效率。
本文使用的节点匿名算法首先要将节点进行社区划分,然后分别进行节点的匿名保护,算法在执行时会多次遍历,通过改变k值可以增加匿名强度。
算法1节点分类k度匿名算法(K-Ca)
输入G=(V,E),M={C1,C2,…,Cm},社区序列CNk,result
输出匿名后的k度匿名图G′=(V′,E′)
1.V←{v1,v2.…,vn},E←{(vi,vj)|i≠j},k←3,result←1
2.while result < k-1
3.for i←1 to m
4.x←v.neighbors∉Cv(v∈Ci)
5.result←count(unique(x))sss
6.if result < k-1
7.select a node u∉Ci
8.if G.edge(u,v)∈G
9.then reselect a node u
10.G.add edges(u,v)
11.end if
12.end if
13.end for
14.end while
15.for i←1 to m
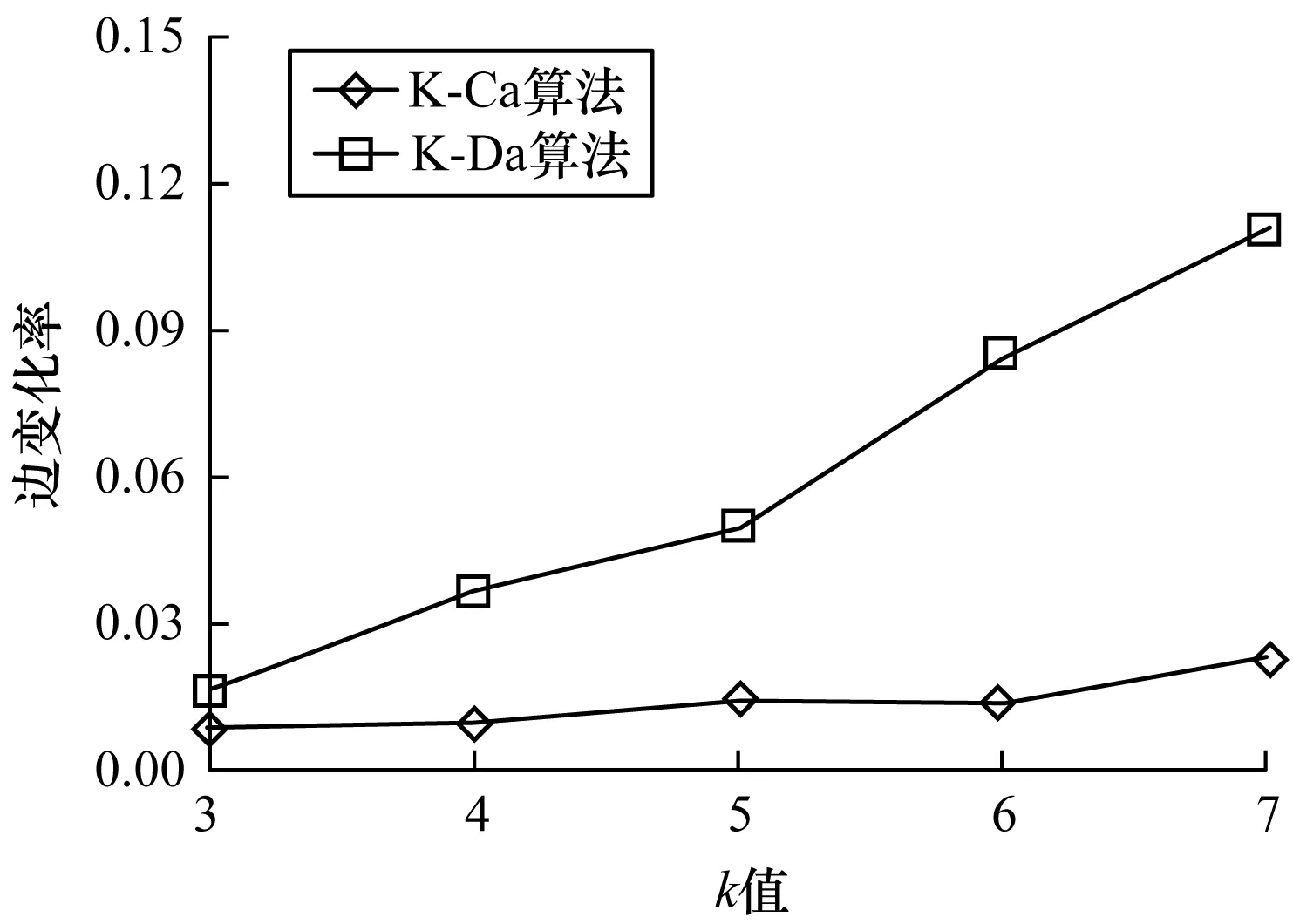
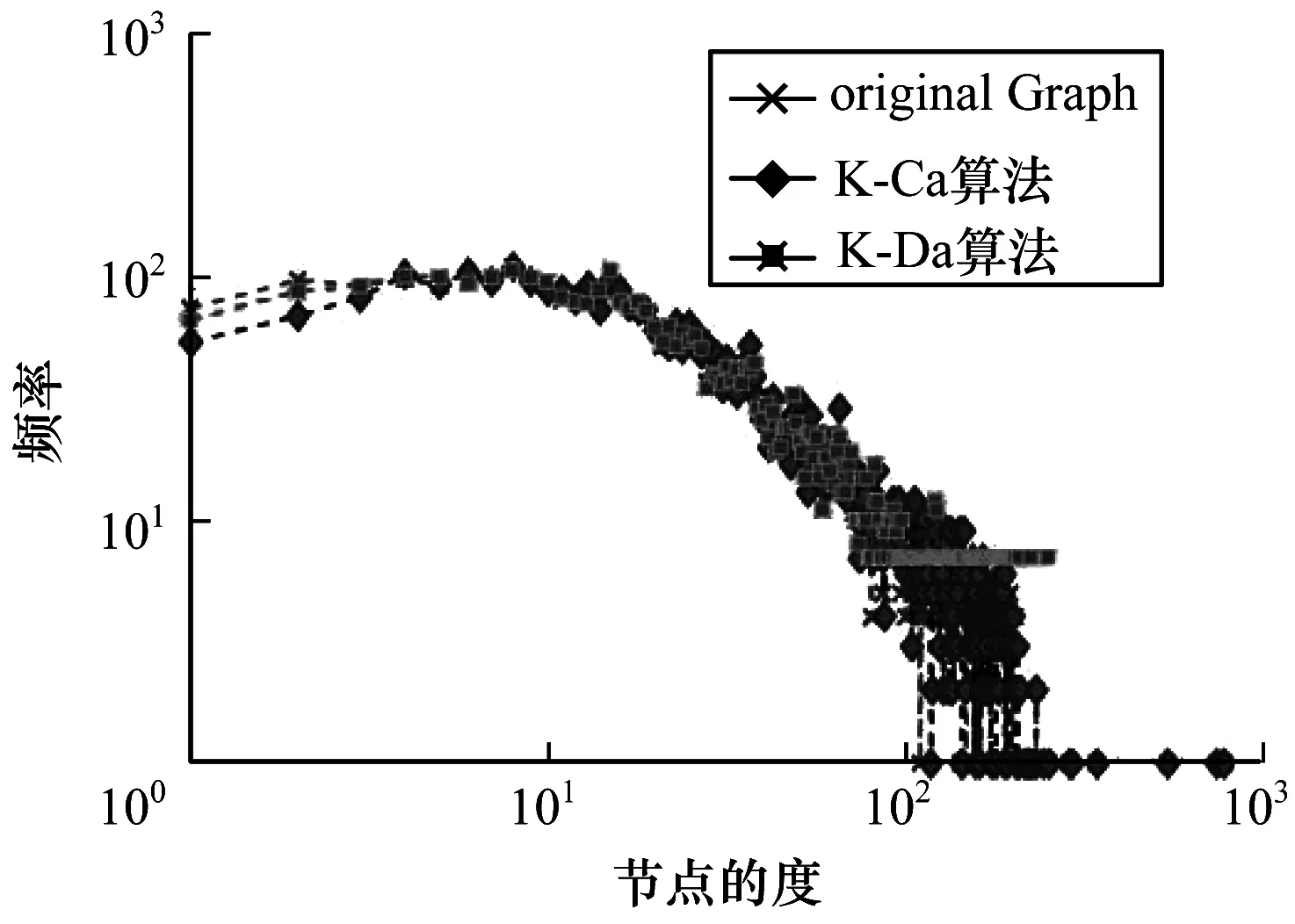
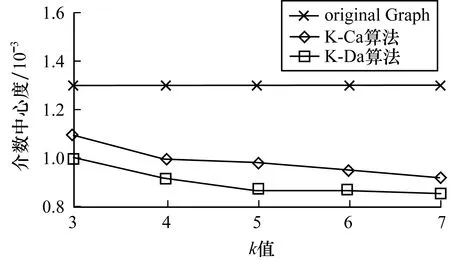
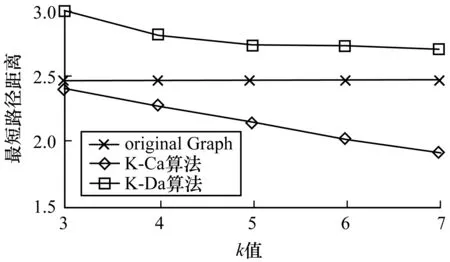
16.while count(unique(cni)) 17.for j←1 to length(Ci) 18.count deg(xi) 19.select a node y∈Ci 20.G.add edges(x,y) 21.end for 22.updateLi 23.end while 24.end for 在上述算法中,result用来记录当前边缘节点的社区数,初始化节点社区编号的时间复杂度为O(n),而后随机选择节点进行社区数序列匿名,不断在社区间进行迭代操作,时间复杂度为O(ml)(m是社区个数,l是边缘节点个数)。在一般情况下,ml比节点数n要大,因此该算法的时间复杂度为O(ml)。 本文提出的匿名方法将原始图G=(V,E)转变为匿名图G′=(V′,E′),节点集合V=V′,而边集合E≠E′。节点分类k度匿名算法对边的修改是动态的,对不满足匿名条件的节点才会有选择地进行边的增加或者删除,因此,从边的修改程度来衡量信息的损失度,通过计算图G′和图G中变化的边的数目占原始图G中边的总数的比例来衡量数据的损失。计算公式如下: (2) 基于信息损失度衡量数据实用性,信息损失值Loss(G)越大,数据实用性越低。 本文通过实验验证社区划分算法和匿名算法的准确性并对其实验结果进行分析。所有实验均在Windows10系统下完成,配置为16 GB的RAM和3.40 GHz的8核处理器。 本文主要使用两个数据集:1)Football数据集,该数据集是由Girvan和Newman根据美国大学足球队之间的关系收集整理得到,包含115个节点、613条边;2)Facebook数据集,来源于 Stanford大学的一个公开数据库SNAP[18],该数据集说明了Facebook社交网站上各用户之间的关系,包含4 039个节点、88 234条边。本文对数据集先做了预处理再进行社区划分,得到多个子图的结构数据。 对于社交网络中的数据,在匿名隐私保护的同时需保证其实用性。为验证本文匿名算法的正确性与有效性,通过计算边的变化率来说明数据的信息损失度,若数据的信息损失度越小,则数据的实用性越好。另外,本文还考虑了图结构的一些基本属性,主要测试指标为度分布、聚类系数、介数中心性、最短路径等[19-20]。将匿名前后的数据进行对比,验证本文提出匿名算法的正确性。 图5对比分析了本文提出的节点分类k度匿名算法(K-Ca)和传统k度匿名算法(K-Da)在匿名前后数据的信息损失度。可以看出,两种算法的数据损失度均较小,但是相比于K-Da算法,K-Ca算法具有更小的数据损失度(低于2%),数据实用性更高。 图5 信息损失度 图6展示了Facebook数据集匿名前后的度分布情况,original Graph表示原始图。匿名前后的图数据的度分布基本保持一致,说明本文算法最大程度保留了节点的连接关系。 图6 Facebook数据集的度分布(k=3) 图7展示了不同k值下社交网络图匿名前后的介数中心性变化结果。本文提出的K-Ca算法对介数中心性的影响小于K-Da算法,K-Da算法对图的重构严重影响了图的结构,而K-Ca算法在匿名时从节点本身出发选取边的操作引起的图结构变化非常小。由此可见,K-Ca算法实现匿名的同时最大化地保留了原始图结构。 图7 介数中心性 图8展示了社交网络图中节点之间最短路径的均值变化。可以看出,随着k值的增加,节点间的最短路径都在减小,但是K-Da算法的路径距离大于原始图节点的最短距离,较大程度地影响了节点间的连接关系,造成节点与节点之间更稀疏,而本文的K-Ca算法缩短了路径距离,可保持节点间的连接关系,并且由于对边缘节点的连接关系的修改,使得源节点和目标节点之间可以通过更少的节点进行连通。 图8 最短路径距离 为更好地说明本文节点分类匿名算法具有更强的隐私保护力度,选取LPA快速社区划分方法[21]对匿名后的图数据进行节点社区的重新划分,判断匿名前后社区划分的结果是否一致,社区划分后节点的社区关系是否发生变化。通过对比匿名前后的社区划分结果发现经过匿名后的图在进行社区划分时社区内的节点产生了变化,不再是固定的某些节点划分到一个社区中。图9对比了K-Da算法和K-Ca算法在匿名前后对社区的影响,K-Da算法只对度进行了考虑,却没有考虑节点的社区结构,对节点的社区划分影响较小,攻击者根据社区关系成功识别节点和社区的概率非常大,从而说明K-Da算法对社区关系的影响大于K-Ca算法。k值越大,对社区的影响越大,使得攻击者进行社区划分也不会得到原始的社区结构,从而说明攻击者无法根据社区关系来识别节点或社区,K-Ca算法对社区关系的保护更强于K-Da算法。 图9 社区划分变化 通过对比不同算法的运行时间来说明算法的时间复杂度。在图 10中,当k值较小时,K-Ca算法的运行时间低于K-Da算法,但是随着k值的增加,K-Ca算法的运行时间开始快速增长,超过K-Da算法。由此可知,在一定的k值内,K-Ca算法优于K-Da算法,但是在整体时间复杂度上,K-Ca算法的时间复杂度还是过高,导致效率过低,因此K-Ca算法的时间复杂度仍需做进一步优化。 图10 运行时间对比 本文分析了传统k度匿名算法中存在的问题并结合现有攻击方法,提出基于节点分类的k度匿名隐私保护方法。通过引入社区这一概念,使节点分成边缘节点和一般节点,将边缘节点的社区序列匿名和社区内节点的度匿名,从而完成整个社交网络的k度匿名。匿名后的图通过度和社区关系的保护加强匿名效果,同时提升了隐私保护强度。实验结果表明,本文方法能有效地对数据进行匿名保护,并且能降低数据实用性损失,但在对数据进行匿名保护时,算法时间复杂度过高,如何优化本文K-Ca匿名算法的时间复杂度将是下一步研究的重要内容。2.4 信息损失和实用性度量
3 实验结果与分析
3.1 数据集
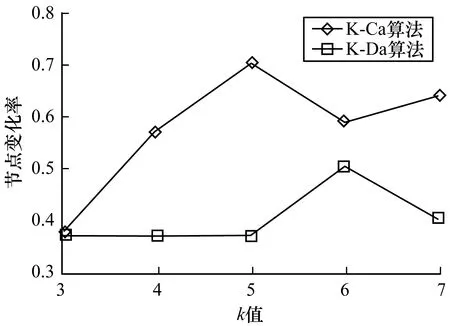
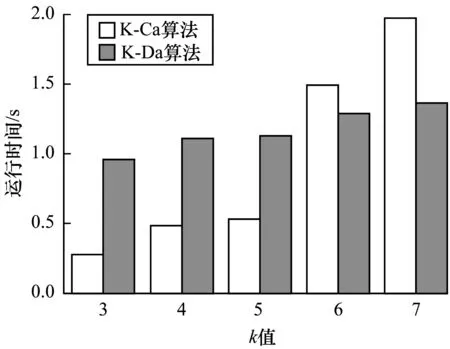
3.2 结果分析
4 结束语

