基于个体模糊作用域的行人流建模与仿真

李世威，王建强，刘应东

(兰州交通大学 交通运输学院，兰州 730070)

行人流应急疏散问题在理论界是一个研究热点[1-2].目前，关于行人流研究在行人流场景构建、行人流建模和控制实验等方面都取得了丰富的研究成果.Helbing等[3]通过研究行人在运动过程中所产生的力场及其之间的交互作用，提出了社会力模型，为行人流建模提供了理论基础.Burstedde等[4]基于社会力模型的思想，构建了著名的二维元胞自动机模型，即场域模型(floor field model,FFM)，模拟了行人流“阻塞聚集”、“拱形”、“快即是慢”等自组织现象.之后，很多学者研究了场域模型的改进与扩展，例如文献[5-6]借助生物学仿真的思想来描述行人之间的相互作用，改进了场域模型；宋卫国等[7]通过引入行人摩擦力和排斥力的量化函数，扩展了场域模型.此后，部分研究者在行人摩擦、推撞和越行等方面做了大量细致的分析，有效改进了场域模型[8-9].也有研究者为了提高场域模型的模拟精度，将行人流疏散场景离散化为更小的网格，假设行人可以同时占据多个网格，使得对个体微观行为特征描述更为精细、准确[10-11].除了对场域模型改进研究之外，近年来，一些研究者通过疏散演习实验来获取场域模型的关键参数，使行人流模拟更加符合现实情况[12-13].然而，对行人作用域的定义，绝大多数模型只是统一划分一个固定大小的区域，忽略了行人在区域大小选择上的异质性[4-13].如何体现行人流模拟过程中个体的差异性，就需要对既有行人流模型进行精细化改进，使得模型能够更加贴近行人的运动特征，以便深入研究行人微观运动特征对疏散效率的影响.

基于此，在场域模型的基础上，为描述行人在作用域选择上的差异性，通过控制实验的实测数据，定义行人运动过程中的模糊作用域，分别计算行人在模糊作用域中个人空间与信息处理空间内的作用力参数，以及个体邻域相对移动距离参数，对不同情况下行人流演化进行仿真研究，分析系统规模、安全出口宽度、行人密度和策略选择对行人疏散效率的影响.

1 模糊作用域

行人的运动行为具有复杂性和异质性，行人通过在其作用域内与其他行人的交互进行邻域位置选择.多数文献通过采用固定大小的圆形来定义作用域形状和大小[14-15].然而，由于行人在诸如社会角色、性别、知识水平、认知能力、心理特征等方面的差异性，影响了个体对作用域范围的判定.不同行人在确定作用域范围时，并不是传统场域模型中所标定的无差异.因此，为提高场域模型的模拟精度，就需要重新定义行人作用域.

假设行人在运动过程中，在任意时刻下可选择的位置为Moore邻域，个体在邻域中的运动方向和各邻域的坐标如图1所示，其中0表示行人原地等待.

基于文献[16-17]控制实验的实测数据和研究结论，将行人最大作用域标定为半径等于5个网格长度的圆型，在Moore邻域中行人可以朝8个方向运动，进而个体位置选择受8个方向作用域(directional action field,DAF)的影响，且每个DAF的最大范围为90度，如图2所示.

为了定义DAF最大范围，以行人为坐标原点构建二维坐标系，该行人8个方向的角度分别为θ1=π/4，θ2=π/2，θ3=3π/4，θ4=π，θ5=5π/4，θ6=3π/2，θ7=7π/4，θ8=0或2π.设定在作用域中，∀网格到坐标原点的夹角为θ.行人通过θ与8个方向的角度θd(d=1,2,…,8)的差值，来判定该网格属于哪个DAF，如果θ与θd差的绝对值在[0,π/4]范围内，则判定该网格在方向d的作用域中.其计算公式可表示为

(1)

其中：x表示DAF网格判定系数.

通过文献[16-17]的实证分析，发现行人对DAF范围的判定是一个模糊概念，并通过实测数据模拟x的模糊函数近似服从降半岭形分布，可表示为

(2)

其中：Ad(x)表示x的模糊函数.

为了刻画行人在DAF选择上的差异性，设在Ad(x)上存在∀λ∈[0,1]，定义：

(3)

(4)

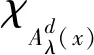
2 模型构建

设行人流场景为(N+1)×(N+1)的二维离散网格系统，N×N表示离散化场景的网格总数，定义N为系统规模，系统边界表示围墙W，安全出口只能设置在系统边界，即围墙W上.根据场域模型的基本假设，仿真过程被离散化为等长的时间步，在任意时间步每个网格要么仅被一个行人占据要么为空.根据以往研究经验，设置时间步长为0.5 s.行人根据设定的行人密度随机分布在网格系统中，安全出口处不设置行人，在每个时间步行人只能占据一个网格，行人只能通过安全出口离开系统.

2.1 个人空间的排斥力

行人在运动过程中通常倾向与其他行人保持一定距离，如果与他人距离过近，行人就会有拥挤感，也就是说人与人之间存在一种互相排斥的力，将这种个人所拥有的斥力场称为“个人空间”.因此，行人在作用域中，会与拥有较多行人的DAF产生一种排斥力，使得行人有可能放弃该方向邻域的选择.

(5)

(6)

2.2 信息处理空间的吸引力

研究发现，行人在陌生环境或紧急状况下，会有明显的从众心理，行人通过对作用域中信息的获取与反馈，会出现模仿他人运动的行为，也就是说人与人之间存在一种互相吸引的力，将这种行人所拥有的引力场称为“信息处理空间”.因此，拥有较多行人的DAF又会对行人产生一种吸引力.

(7)

(8)

2.3 个体邻域相对移动距离

在任意时间步，行人运动位置的选择会受到个体邻域与安全出口的距离影响，可采用欧式距离来度量每个行人的邻域与安全出口之间的距离.当安全出口的宽度大于一个网格时，取距离最近的安全出口网格进行计算，记：

(9)

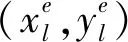
(10)

(11)

2.4 转移概率

系统仿真过程被离散化为等长的时间步，采用并行更行规则，即在每个时间步行人根据DAF中个人空间的排斥力、信息处理空间的吸引力和个体邻域相对距离的参数计算，共同确定个体邻域的转移概率.设∀行人i在当前时间步的坐标为(x,y)，该行人的转移概率为

(12)

2.5 行人策略选择

在行人运动过程中，由于行人的差异性会导致个体所选取的运动策略不同.模型主要研究在现实生活中应用最为广泛的两种策略：

1) 相互竞争策略：当多个行人同时选择进入一个网格时，为了体现行人的相互竞争性，系统以相同概率随机选择一个行人进入，没有被选中的行人保持位置不变.该规则说明每个行人都以相同的概率选择自己的运动线路，从而实现相互竞争的运动目的.

2) 相互让步策略：当多个行人同时选择进入一个网格时，系统选择个体转移概率最大的行人进入，如果存在多个最大转移概率的行人，则以相同概率随机选择一个个体进入，没有被选中的个体保持位置不变.该规则说明转移概率低的个体对转移概率高的个体做出让步，从而实现相互让步的运动目的.

2.6 行人更新规则

在仿真过程中系统遵循以下行人更新规则：

1) 每个行人只能在当前时间步下的Moore邻域中进行位置选择；

2) 并行计算每个行人邻域网格的转移概率；

3) 行人选择转移概率最大的邻域作为其目标位置；

4) 当邻域中存在多个最大转移概率网格时，则以相同概率随机选择一个网格作为其目标位置；

5) 当多个行人同时选择进入一个网格时，系统分别采用相互竞争策略和相互让步策略进行模拟；

6) 当行人运动到安全出口时，在下一时间步离开系统；

7) 当所有行人都离开系统后，仿真过程结束.

3 仿真分析

系统中的行人密度K定义为行人总数与场景网格总数N×N的比值；安全出口宽度L定义为安全出口所占的网格数；行人疏散时间T定义为所有行人离开系统时所需的时间步.采用20次运行结果的平均值来减少参数初始设置对仿真结果的影响.

在系统规模N=10,20,30,40，单个出口在围墙中间位置的情况下，分别采用相互竞争和相互让步两种策略，对行人疏散时间T与行人密度K之间的函数关系进行仿真研究，模拟结果如图3～4所示.

图3描述了在不同系统规模下，采用相互竞争策略，安全出口分别为1和10个网格宽度时，行人疏散时间随行人密度的变化趋势.图4描述了采用相互让步策略时，行人疏散时间随行人密度的变化趋势.

在L不变的情况下，行人疏散时间随行人密度的增加近似呈线性递增函数关系.不同系统规模下的行人疏散时间存在显著差异.个体在不同行人密度下采用不同的运动策略，对行人疏散时间也有显著影响，但行人疏散时间与行人密度之间的线性关系和系统规模、运动策略无关.

在系统规模N=20,30、不同安全出口宽度、且单个出口在围墙中间位置的情况下，分别采用相互竞争和相互让步两种策略，对行人疏散时间T与行人密度K之间的函数关系进行仿真研究，模拟结果如图5～6所示.

图5描述了在不同安全出口宽度下，采用相互竞争策略，系统规模为20和30时，行人疏散时间随行人密度的变化趋势.图6描述了采用相互让步策略时，行人疏散时间随行人密度的变化趋势.

在N不变的情况下，不同安全出口宽度的行人疏散时间存在显著差异；行人疏散时间和行人密度之间的线性关系与安全出口宽度无关.

在系统规模N=10,20,30,40，单个出口在围墙中间位置的情况下，当行人密度K=0.4,0.6时，分别采用相互竞争和相互让步两种策略，对行人疏散时间T与安全出口宽度L之间的函数关系进行仿真研究，模拟结果如图7～8所示.

图7描述了在不同系统规模下，采用相互竞争策略，行人密度为0.4和0.6时，行人疏散时间随安全出口宽度的变化趋势.图8描述了采用相互让步策略时，行人疏散时间随安全出口宽度的变化趋势.

在K不变的情况下，行人疏散时间随安全出口宽度的增加近似呈负指数性减少函数关系；系统规模越大或安全出口越窄，行人疏散时间就越长；系统规模和行人密度不变，行人疏散时间随安全出口宽度的增加会显著减少.

为了研究不同策略对行人疏散时间的影响，在采用相互竞争策略和相互让步策略、系统规模N为20和30、行人密度K为0.4和0.6的仿真场景中，对行人疏散时间随安全出口宽度变化的函数关系进行仿真研究，模拟结果如图9所示.

采用不同的运动策略对行人疏散时间和安全出口宽度之间的负指数型曲线变化有显著影响，当安全出口宽度较窄时，让步策略比竞争策略具有更好的疏散效果；随着安全出口宽度的增加，让步策略和竞争策略的优越性会发生逆转；当安全出口宽度足够大时，让步策略和竞争策略的优越性无显著差异.

4 模型对比分析

为了验证改进模型的有效性，分别对采用相互竞争策略、系统规模N=60、500个行人随机分布在系统中，在文献[5]、[14]、[15]模型和改进模型的仿真下，行人疏散时间随安全出口宽度变化的函数关系进行仿真研究，如图10所示.从图10可以看出，当安全出口较小时，改进模型的模拟结果优于文献[5]、[14]、[15]的模型；当安全出口足够大时，改进模型的模拟结果优于文献[5]的模型，略优于文献[14]、[15]的模型.此外，文献[5]、[14]、[15]模型仅考虑竞争策略下的行人流疏散，并没有考虑让步策略下的行人流疏散.由此可见，改进模型不仅在疏散效率上有所改进，而且在疏散策略上做了进一步拓展性研究.

5 结论

基于场域模型，通过定义方向模糊作用域中个人空间和信息处理空间内的作用力参数，充分考虑了个体在方向作用域选择上的差异性，构建了一个单出口行人流运动场景，分别采用相互竞争策略和相互让步策略，对行人流运动进行了仿真研究.通过与既有场域模型的对比分析，证明了改进模型的有效性.研究结果表明，通过参数的标准化处理，使得仿真模型不依赖于各因素的影响系数，就能够有效模拟行人流疏散过程.研究显示，行人疏散时间与行人密度近似呈线性增加函数关系，与安全出口宽度近似呈负指数性减少函数关系，系统规模的大小对行人疏散时间有显著性影响.行人运动策略选择对行人流运动效率有不同的影响，当安全出口宽度较窄时，让步策略比竞争策略具有更好的疏散效果；随着安全出口宽度的增加，让步策略和竞争策略的优越性会发生逆转；当安全出口宽度足够大时，让步策略和竞争策略的优越性无显著差异.该研究可以为单一出口或单一瓶颈处行人设施的疏散策略制定提供参考.

本研究只考虑了在单一出口场景中，没有障碍物，且行人视线不受影响的情况下，行人流的动态演化过程.对于多出口场景、障碍物的设置、行人视线受限等情形，都是值得进一步研究的方向.