运载火箭电动伺服机构前馈自抗扰控制方法的设计

胡翔宇，于 戈，曾凡铨，崔业兵

(上海航天控制技术研究所，上海 201109)

0 引言

永磁同步电机(Permanent Magnet Synchro-nous Motor，PMSM)因具有功率范围宽、效率高、低速大扭矩、使用维护方便及静音性等多种优点，在航空航天等伺服系统领域应用广泛，特别是在新一代运载火箭中已更多地开始采用PMSM作为电动伺服机构的驱动电机。航天用伺服机构一般为位置闭环系统，PMSM作为驱动系统的被控对象，通常采用电流环、速度环和位置环三环，并在每环加入相应的控制策略来实现伺服机构的位置闭环控制。控制策略一般采用传统的PID控制算法，而在输入信号为正弦波且伴随有力矩干扰的情况下，仅靠PID控制策略较难同时满足系统的刚度和跟踪精度需求。针对PMSM的控制难点，目前已经有自适应控制[1]、非线性PID控制[2]、滑模变结构控制[3]和模糊神经网络控制[4]等多种先进控制策略应用于调速系统中。以上方法虽然对外界扰动有抑制作用，但是都有各自的局限性。滑模变结构控制的固有抖动问题是实际应用中的难点，自适应控制和模糊神经网络控制对处理器(Micro Controller Unit，MCU)的性能要求较高，因此均难以运用在运载火箭的伺服产品上。

近年来，研究人员提出了一种工程应用性较强的非线性控制方法——自抗扰控制(Active Distur-bance Rejection Control，ADRC)[5-9]，该控制策略通过扩张状态观测器(Extended State Observer，ESO)统一观测系统外部干扰和系统内部参数变化引起的干扰并加以补偿，具有较好的动态和静态特性，目前已经广泛应用于各领域的伺服系统中。在ADRC的基础上，采用非线性误差反馈的方法，如有限时间比例(Finite Time Proportional，FTP)的控制策略，均可以提高伺服系统的刚度，具有较强的抗扰能力[10-13]。

关于自抗扰设计的大多数文献主要研究的是系统的阶跃响应，在实际应用过程中，如果指令是正弦输入信号，位置反馈对指令的跟随会有较大的误差。通过对控制理论的分析发现，如果输入信号是时变的，那么建模时对输入的近似过程将产生误差，而且产生的误差无法通过ESO进行观测和补偿，导致系统的跟踪误差变大。考虑到微分具有预测误差变化趋势的作用，通过引入输入微分前馈可以减小建模误差，提高系统的跟踪精度。文献[14-15]研究了一种改进型的自抗扰控制器，即在速度环中加入了输入微分前馈环节，而运载火箭用伺服机构是位置跟随性伺服，速度环加入输入微分前馈对位置闭环的跟踪精度影响较小。

针对运载火箭伺服机构对抗扰性能和位置跟踪性能均有较高要求的情况，本文在位置输入为正弦信号的前提下，比较了系统在FTP+ESO控制方式下有无位置输入微分前馈(Proportion Integra-tion Differentiation Feedback，PIDF)的跟踪性能，同时对系统的动态特性也进行了分析。仿真和实验结果均表明，在ADRC中引入PIDF不仅可有效提高系统对时变输入信号的跟踪精度，还可以提升系统的动态特性。

1 PMSM的自抗扰控制器设计

1.1 位置环的数学模型

永磁同步电机的机械运动方程为

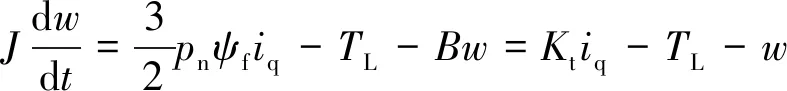
(1)

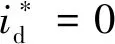
1.2 扩张状态观测器设计

位置环采用扩张状态观测器时，其输出的倒数趋近于无穷大，不满足要求的稳定性条件，因此位置环不适宜使用扩张状态观测器；电流环加入扩张状态观测器对系统性能影响较小，因此电流环也不适宜使用扩张状态观测器。故本文将在速度环中使用扩张状态观测器。

(2)

式中，ws为角速度的基准值。令

选取电机转速w作为状态变量x1，扰动a(t)作为扩张状态变量x2，则状态方程变为

(3)

相对应地,简化二阶线性扩张状态观测器为

(4)

由此得到ESO的结构框图如图1所示。

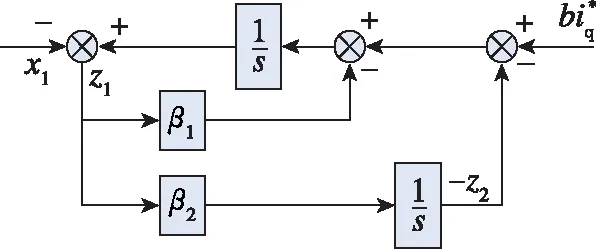
图1 ESO结构框图Fig.1 ESO structure block diagram

1.3 误差反馈控制律设计

将跟踪误差定义为θerr=θ-θf，其状态方程为

(5)

其中，状态变量x2需由z1代替，得到

(6)

希望跟踪误差按式(7)所示的规律进行衰减

(7)

其中，k为控制器的比例系数，用于控制误差的衰减快慢。非线性函数定义如下

(8)

函数中α为非线性指数，δ为平衡点附近的线性区范围。结合式(6)和式(7)可得控制量为

(9)

结合式(7)和式(8)可知，当0<α<1时，跟踪误差θerr可以在有限时间内衰减到0，因此称为FTP控制，形成FTP+ESO的复合控制方式；当α=1时，非线性函数将退化为线性函数，反馈控制律变为比例控制(P)，形成P+ESO的复合控制方式。

2 系统的跟踪性能分析

2.1 ESO性能分析

由图1可解算出，x1到z1的传递函数为

(10)

当控制量为恒定值时，即控制量的导数s*u(s)=0时，得出

(11)

由式(11)可以看出，z1是对x1的低通滤波。由此可知，控制量为0的ESO可作为滤波器使用。

由图1还可解算出，x2到z2的传递函数为

(12)

由式(3)、式(5)、式(9)可得出跟踪误差的状态方程为

(13)

系统的稳态误差为

(14)

2.2 PIDF对系统的影响

对于输入信号时变的情况，dθ/dt也为时变量。由式(14)可以看出，系统的稳态跟踪误差不仅与ESO的观测误差z2-x2有关，还和输入角度的变化律有关。

系统加入PIDF后，控制量为

(15)

由式(3)、式(5)和式(15)可得跟踪误差方程为

(16)

稳态跟踪误差为

(17)

比较式(14)和式(17)可知，系统加入PIDF后跟踪误差只和ESO的观测参数相关，与输入形式无关，减小了系统的跟踪误差。

考虑电流限幅的影响时，实际控制量为

(18)

由此可得位置环自抗扰控制器的结构框图如图2所示。

图2 位置环ADRC控制器Fig.2 Position loop ADRC controller

PMSM基于矢量控制的自抗扰调速系统的原理框图如图3所示。

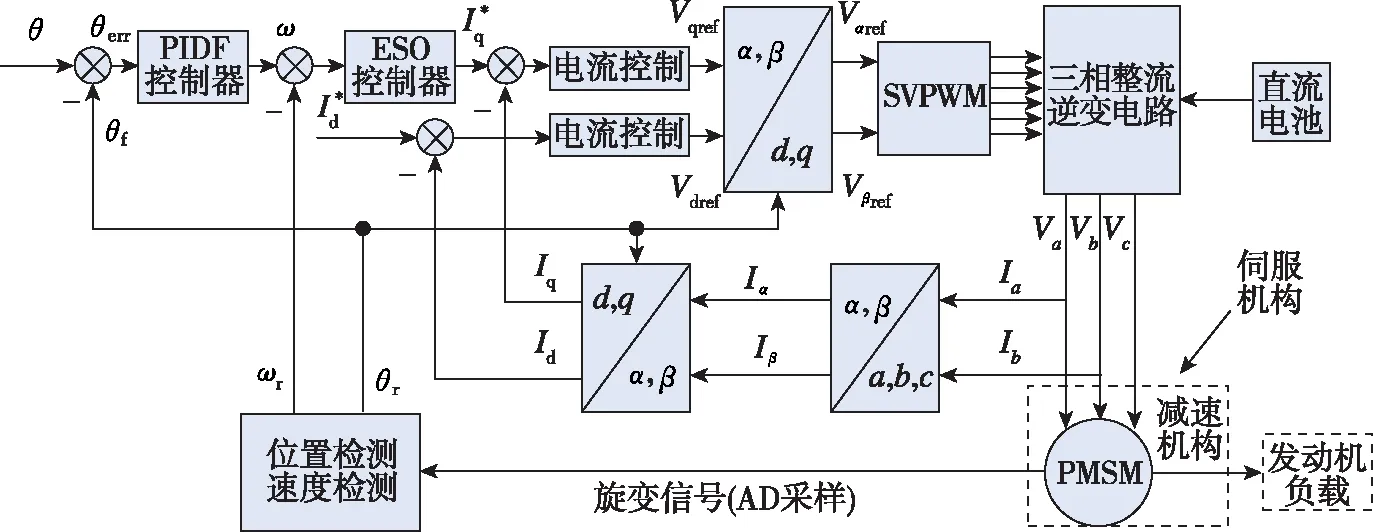
图3 位置自抗扰控制系统结构框图Fig.3 Structure block diagram of position ADRC system

3 仿真分析

为了验证以上设计方法的正确性，首先对电机与测功机系统的转动惯量进行辨识；然后在频率为1Hz的正弦输入信号条件下，分别对FTP+ESO控制策略下有无输入微分前馈时的跟踪性能和幅频特性进行仿真；最后比对仿真结果。

测功机系统通过对电机加载力矩并测量电机角加速度，利用转动惯量、输出力矩和角加速度三者之间的关系得到电机的转动惯量，见式(19)

J=Te/α

(19)

其中，J为转动惯量，Te为加载力矩，α为角加速度。

本项目中采用的电机参数如表1所示。

表1 电机参数Tab.1 The motor parameters

实际加载中采用伺服机构的额定负载，即负载为4N·m。控制器参数设置为：k=17，keff=19.7，δ=0.01，p0=500。电流环中的PI控制器参数设置为kpi=0.1，kii=500。

仿真参数如表2所示。

表2 仿真参数Tab.2 Simulation parameters

仿真结果如图4和图5所示。

图4 FTP+ESO控制下正弦输入时的动态响应(仿真)Fig.4 Dynamic response to sinusoidal input under FTP+ESO control (Simulation)

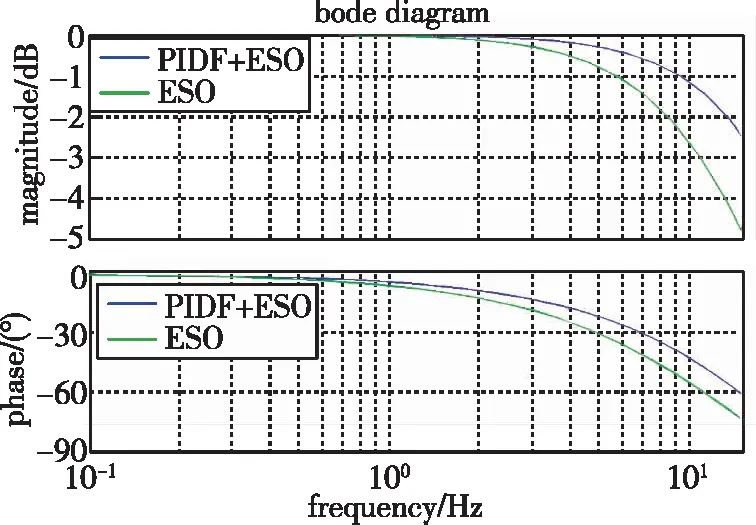
图5 FTP+ESO控制下的幅频和相频曲线(仿真)Fig.5 Amplitude frequency and phase frequency curves under FTP+ESO control (Simulation)

通过图4可以看出，在FTP+ESO控制策略下，若没有输入微分前馈时，系统有2°的跟踪误差；当加入输入微分前馈时，FTP+ESO的反馈曲线和信号曲线基本一致。通过图5可以看出，当自抗扰系统加入PIDF后，系统幅频和相频的带宽均有一定程度的提升。

同时，为验证加入PIDF算法后系统依然具有较强的抗干扰能力，对系统的抗干扰性能再次做了仿真比对。系统在1s时刻，加入1N·m的恒值干扰力矩，对比传统PID算法和加入PIDF后的自抗扰算法的抗干扰性能，仿真结果如图6所示。

图6 系统抗干扰性能对比(仿真)Fig.6 Comparison of disturbance rejection performance of the system (Simulation)

4 试验验证

为验证以上的理论分析和仿真结果，本文继续进行了试验分析。试验平台主要由伺服机构、dSPACE半实物仿真平台和弹簧杆加载设备组成。试验中的PWM载波频率设置为10kHz，通过位置闭环实现PWM占空比的实时调节。

系统的硬件结构框图和实验平台分别如图7和图8所示。

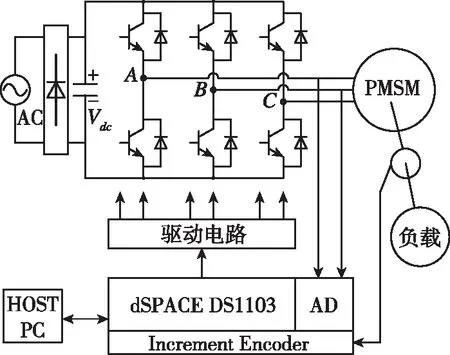
图7 系统硬件结构框图Fig.7 System hardware structure block diagram

图8 实验平台Fig.8 Test platform

试验中，算法使用仿真中的各项参数，跟踪性能验证时，采用5°、1Hz的正弦位置输入信号；幅频性能验证时，采用幅值为0.5°、0.1～10Hz各频率点扫频。

为验证FTP+ESO控制器作用下系统的跟踪时变输入信号的性能，对跟踪给定正弦角度输入的实验结果进行了对比。先使电机在无输入微分前馈的控制方式下跟踪正弦给定，待PMSM运行稳定后，通过切换控制模式使电机运行在有输入微分前馈的控制方式下。由图9可以看出，FTP+ESO控制下没有加入PIDF时有2°的跟踪误差，加入PIDF时的系统跟踪误差仅为0.08°。

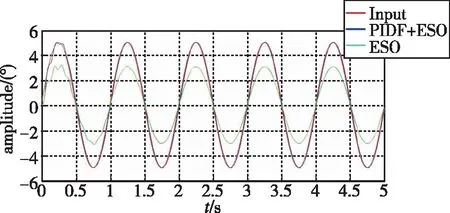
图9 FTP+ESO控制下正弦输入时的动态响应(试验)Fig.9 Dynamic response to sinusoidal input under FTP+ESO control (Test)

表3所示为对比自抗扰控制有无加入PIDF策略时各频率点(0.1～10Hz)扫频的幅值和相位的数值。从表3可以看出，自抗扰控制加入PIDF策略后系统的动态特性有较大程度的提高。

表3 动态特性数据(试验)Tab.3 Dynamic characteristic data (Test)

由试验结果可以看出，引入输入微分前馈可以有效提高对时变位置信号的跟踪精度和系统的动态特性。

5 结论

利用FTP控制和扩展状态观测器以及位置输入微分前馈相结合的自抗扰控制策略，对运载火箭电动伺服机构用永磁同步电机的位置跟踪性能和动态特性进行了研究。针对正弦位置输入信号的情况，通过加入位置输入微分前馈环节，消除了建模误差，有效降低了伺服机构对正弦位置信号的跟踪误差，并提升了系统的动态特性，同时系统仍然具有较好的抗干扰性能。严格的理论分析表明，该方法可以提高伺服系统的跟踪性能。最后通过仿真和实验结果比较验证了该方法的有效性。