AUV的图优化海底地形同步定位与建图方法
马 腾,李 晔,赵玉新,沈 鹏,凌 宇
(1.哈尔滨工程大学水下机器人技术重点实验室,哈尔滨 150001;2.哈尔滨工程大学自动化学院,哈尔滨 150001;3.国家深海基地管理中心,青岛 266237)
0 引言
随着人类对海洋探索和开发需求的日益旺盛和多波束测深声纳技术的不断成熟,构建高精度的海底地形图已经成为了帮助人类了解海洋和开发海洋的重要手段。受多波束声纳等声学测绘仪器的工作特性(1.声波作用范围有限;2.测绘精度与载体到海底的距离有关)限制,智能水下机器人(Autonomous Underwater Vehicle,AUV)作为一种能够实现大潜深自主航行和自主作业的水下航行器,已经成为了海底地形测绘的重要载体。
AUV在进行海底地形测绘时,精确的实时导航信息尤为重要。AUV在水下作业时,无法同卫星进行通信获取准确的位置,推算导航系统则会存在累计误差无法消除的问题。目前,常用的水声定位系统如长基线存在基阵布设困难,校正基阵位置耗时耗力;而超短基线与母船通信延迟受距离影响,在大深度时延迟较大,定位的实时性也无法保证,且AUV作业范围受限于母船活动范围[1-3]。
同步定位与建图(Simultaneous Localization and Mapping,SLAM)是机器人在陌生环境下依靠自身传感器进行定位与同时地图构建的过程,可以从本质上提高无人系统的自主性。由于信息源广泛且容易获取,目前SLAM已经在陆地和空中机器人中得到了较为深入的研究[4-5]。但受水下环境与感知设备条件的限制,水下SLAM的研究尚不成熟,依然存在很多问题。
目前,关于水下SLAM的研究主要以机械扫描声纳[6-7]或水下摄像机[8-9]为环境感知设备。但采用机械扫描声纳的SLAM以堤坝等人造环境为信息源,只适用于港口等结构化环境。而在海洋环境中,结构化环境极为罕见,这极大地限制了前视声纳SLAM的应用。同时,绝大部分的水下环境是光学传感器的弱视区甚至是盲区,光学SLAM在深水区或水质浑浊区域同样很难开展。
在这种情况下,利用多波束声纳作为传感器进行海底地形SLAM(Bathymetric SLAM,BSLAM),由于其应用范围广、可靠性高等特点,已经成为了解决AUV水下精确定位与导航问题的可行手段。Roman[10]提出了使用将点云地图划分为假设导航误差各不相关的一系列子地图,各个子地图间通过地形匹配的方法获取数据关联,通过延迟卡尔曼滤波进行求解。Palomer[11]在扩展卡尔曼滤波器SLAM方法的基础上,考虑测深点和机器人位姿的不确定性,建立了迭代最近点法的概率学表达方式,并将其分为了点-点匹配和点-面匹配2个阶段。Barkby[12-13]基于粒子滤波器提出了使用轨迹地图的BPSLAM(Bathymetric Distributed Particle Filter SLAM)方法,BPSLAM通过建立高斯过程模型,将测线长度的不确定性变为测点处水深的不确定性,从而对测点处水深进行估计,并根据估计值与实际测深值的似然程度,计算粒子权重。可以看到,目前对于海底地形SLAM算法框架的研究主要集中于滤波方法,滤波方法求解方法简单有效且效率高,但需要对AUV的运动模型进行准确建模。而受高阶水动力系数的影响,AUV运动模型的准确建模是极为困难的。
Lu与Milios[14]提出的图优化的方法,通过保留所有的观测数据帧以及帧间的空间约束关系,并将约束看作是随机观测,然后采用最大似然方法估计机器人的位姿,这种思想可以通过图的方式形象地表现出来。使用图优化的方法,通过使用AUV位姿数据和传感器观测数据构建图,通过对图进行优化求解海底地形SLAM,在一定程度上摆脱了运动模型和观测模型的限制,从而解决了AUV运动模型和传感器观测噪声不准确的问题。受多波束声纳物理特性限制,相邻时刻测深数据间无信息冗余,无法建立相邻帧间数据关联,导致传统图优化算法中建图一致性被破坏,需要对传统图优化算法进行改进。
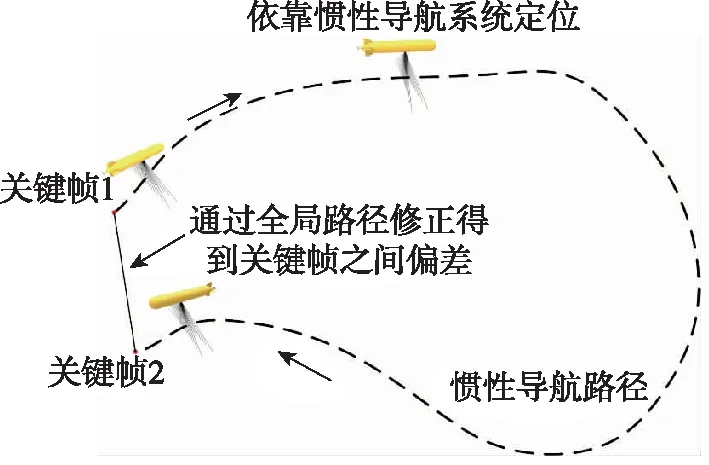
本文提出了一种基于图优化的海底地形SLAM算法,该方法共包括位姿图构建和优化2个部分,位姿图构建中利用水深预测手段和地形匹配方法进行帧间数据关联构建和闭环检测。在图优化过程中,构建全局路径修正和局部路径修正相结合的优化算法框架,对海底地形同步定位与建图问题进行求解。相较于传统的滤波器海底地形SLAM算法,该算法无需对运动模型进行准确建模,计算精度较高,且通过构建位姿图保留了全部历史信息,能够实现对于历史数据的更新、修改等操作。最终通过仿真试验结果对该算法的有效性进行了证明。
1 位姿图构建
1.1 子地图建模
由于多波束声纳仅仅能够获得声学测线的回波时间和回波角度数据,需要将其转化为大地坐标系下的三维测深点信息。为简化计算,通常不考虑AUV在垂直面的运动,即将三维的地图转化为每点代表不同高度值的2.5D点云模型。
如图1所示,由船位推算导航和光纤罗经可以获得AUV位置(xV,yV,zV,θV),其中θV为AUV首向角,对于每一个测点测深侧扫系统会返回声速值,接收到波束的时间值和回波角度的正弦值。通过计算可以得到测线相对于AUV的位置为(r,β),其中r为连接AUV载体坐标系圆心与测点的半径长度,β为相对于zV的有向开角,将其转化为大地坐标系下,公式为
(1)
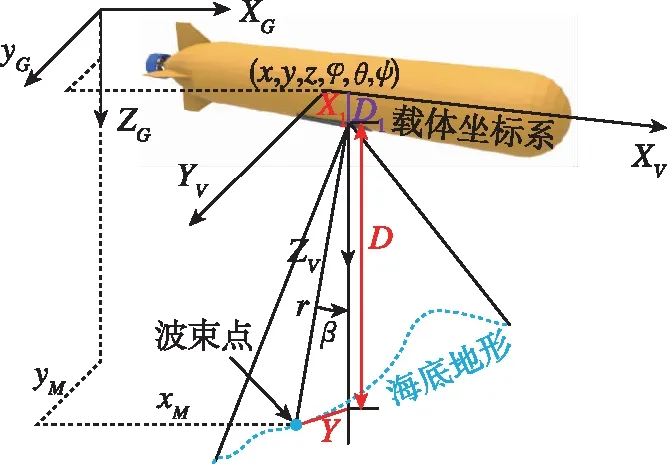
图1 多波束声纳地形测量示意图Fig.1 The schematic diagram of terrain measurement with multi-beam sonar
从而将关联在载体坐标系下的极坐标转化为大地坐标系下带有高度值的2.5D点阵。
考虑到地形匹配耗时的问题,将路径划分为诸多子地图的形式[15]。子地图根据2.5D地图的信息量和路径的长度创建,信息量根据法线间差计算[16]。法线间差利用不同支持半径下的法线值的差值检测有明显变化区域的点云数据,本文中利用其检测地图中地形起伏剧烈区域,计算公式为
(2)
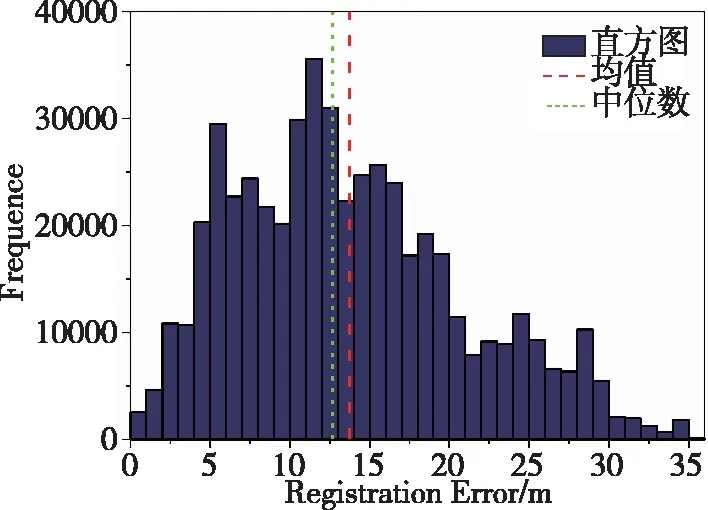
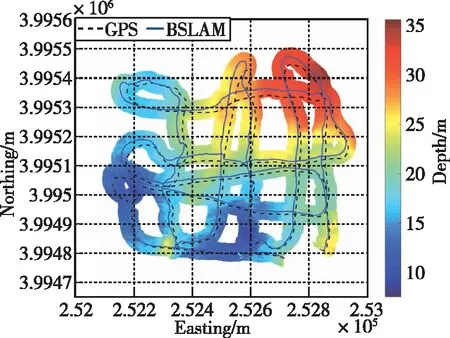
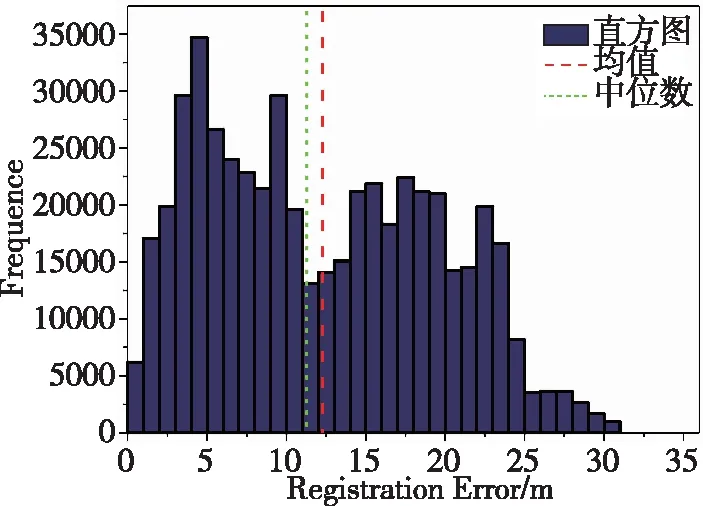
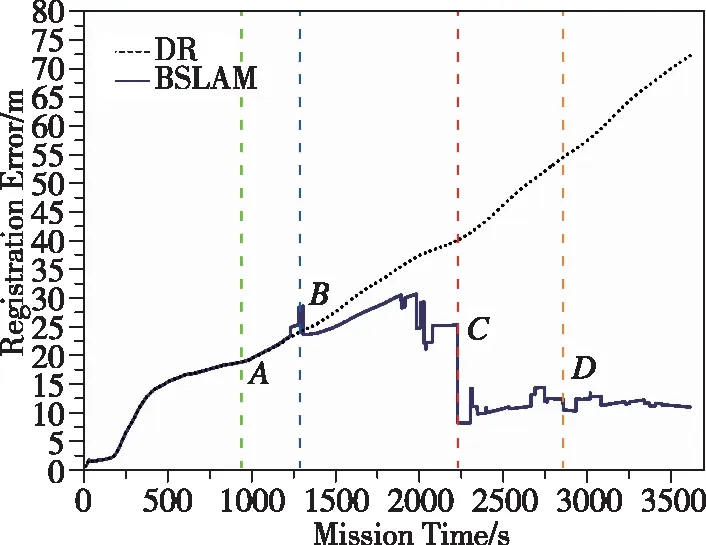
式中,n1、n2分别为支持半径为r1、r2时地形剖面与圆的最外侧交点连线的法线,且满足r1 (3) (4) 图2 闭环检测过程的向量示意图Fig.2 Vector diagram of loop closure detection Xi-Xj=lj-li+Δ-w (5) 若使用在Xi与Xj处的惯性导航偏移量ΔXi和ΔXj代替Xi和Xj,式(5)可以写为 ΔXi-ΔXj=Δ-w (6) 在使用参考文献[18]提出的地形外推方法获得i+1时刻地形外推结果后,可通过与i+1时刻多波束实测数据之间的相似程度对弱数据关联进行求解。结合多波束测量信息,对i到i+1时刻建立状态模型 (7) 因而,弱数据关联p(Xi+1|Xi,ui)可以表示为 (8) 全局路径修正的前提是选取合适的状态转移方程和观测方程。对于AUV而言,存在包括六自由度操纵性方程等多种状态转移方程。但由于一、二阶水动力系数计算困难,SLAM中一般选择简化的运动模型,即 Xi=f(Xi-1,ui)+vi (9) (10) 关键帧i处的导航偏移量连续性方程可以表示为 (11) 因此,可以将导航偏移量连续性方程表示为矩阵的形式 ΔXkey=HΔXkey (12) 另一方面,环形闭合的观测方程也可以表示为 (13) (14) 若将观测方程表示为矩阵形式,可以得到 DS=HSΔXkey (15) 其中,DS代表对所有环形闭合结果观测的集合,ΔXkey为所有关键帧上的AUV导航偏移量,HS则是由1、-1和0组成的系数矩阵。 在得到AUV在关键帧的位置修正结果后,局部路径修正解决的就是如何将通过全局路径修正求得的AUV在关键帧处的导航偏差传递到整条路径上。 (16) 图3 局部路径修正示意图Fig.3 Schematic diagram of local trajectory optimization 需要注意的是,与传统的运动模型不同,ui不再表示控制输入,而是表示i时刻AUV真实的位移,而vi则代表了i时刻AUV惯性导航值相对于真实位移的偏移量。在n时刻AUV惯性导航的偏移量ε可以表示为 (17) 参考弹簧系统,本节提出了一种误差修正方法,同样将AUV各时刻的状态视为弹簧的端点。由于惯性导航系统存在误差,现阶段系统是受力并且不稳定的,其系统能量模型为 (18) θi=-lnp(Xi|Xi-1) (19) 将能量模型转化为受力模型,根据串联弹簧的受力形变公式 =θ1(v1-v0)2=…=θn(vn-vn-1)2 (20) 建立递推模型,依次计算v1一直到vn。 使用中国胶州湾获取的海试数据,试验设备如图4所示,试验数据时长3613s,试验船航速约4节,共行驶约8km。处理后的试验数据以1s为一个数据更新节拍,同时更新AUV状态信息(包括GPS数据、光纤罗经数据)和多波束数据。 图4 海上试验设备Fig.4 Devices in the sea trail experiment 使用船载的多波束声纳、光纤罗经和GPS进行数据获取,其中多波束声纳为GeoSwath Plus,测线宽度约为10倍水深,工作频率为23Hz,斜距分辨率为1.5mm,采样间距为12mm,系统主要包括主控舱和V型架,V型架上装载2个声学发射/接受阵和一个声速计,发送多波束回波数据和声速剖面信息给主控舱。光纤罗经和GPS分别将姿态信息和导航信息发送给主控舱,其中光纤罗经为哈尔滨工程大学研制,姿态测量的精度为0.05°,GPS为NovAtel 公司的ProPak-LB,圆概率定位误差为0.8m。 图5所示为子地图划分的结果,为验证局部路径修正的效果,在对位姿图进行全局路径修正的基础上,分别使用均匀分配方法和提出的局部路径修正算法将关键帧的惯性导航系统偏差分配到整条轨迹上,为便于表示,分别将使用了两种方法的BSLAM算法称为非完全BSLAM(均匀分配)和BSLAM(局部路径修正方法)。为实现对无效闭环结果的剔除,应用了文献[19]提出的投票算法。 图5 子地图划分结果Fig.5 Submap division result 图6(a)、(c)、(e)表示了分别使用惯性导航系统、非完全BSLAM和BSLAM输出的轨迹和构建的海底地形图,而图6(b)、(d)、(f)则是对应的测深点定位误差直方图。误差直方图统计了任务结束后所有时刻测深点位置的误差,以i时刻为例,该时刻所有测深点的误差可以表示为 (21) (a)惯性导航建图结果 (b)惯性导航测点定位误差直方图 (c)非完全BSLAM建图结果 (d)非完全BSLAM测点定位误差直方图 (e)BSLAM建图结果 (f)BSLAM测点定位误差直方图图6 BSLAM位姿图优化结果Fig.6 Graph optimization results in the BSLAM 如图6和表1所示,试验结果证明,全局路径修正和局部路径修正都在BSLAM位姿图优化中起到了重要的作用。相比于非完全BSLAM,BSLAM给出的结果其均值减小了10.82% ,中位数减小了8.87%;而与惯性导航结果相比BSLAM的效果更加明显,BSLAM系统给出的定位误差均值和中位数分别减小了83.13%和82.92%。 表1 测深点定位误差Tab.1 Localization errors of measurement points 如图7所示,AUV在A处第一次成功进行闭环检测,在C处第一次于起始点附近成功进行闭环检测后,一直均将导航误差控制于10m左右。通过试验结果可以证明,全局路径修正和局部路径修正在BSLAM系统中都发挥出了不可替代的作用。 图7 BSLAM实时修正效果Fig.7 BSLAM results in real time 本文针对AUV长时间远距离潜航中的精确导航问题,提出了图优化海底地形同步定位与建图算法。算法分析与实验结果表明: 1)提出了一种基于图优化算法的BSLAM算法,该算法可以实现AUV多波束同步定位与构图,能够有效修正船位推算方法产生的累积误差。 2)BSLAM算法的全局路径修正算法对参考导航系统导航误差的修正起到了最主要的作用。 3)BSLAM算法的局部路径修正虽然只是在全局路径修正结果的基础上实现关键帧导航误差在局部路径上的分配,但仍然可以有效减小AUV定位与建图误差。1.2 闭环检测
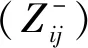
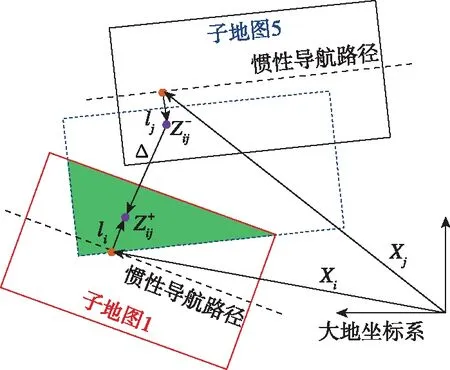
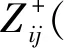
1.3 弱数据关联构建
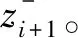

2 位姿图优化
2.1 全局路径修正
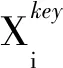
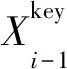

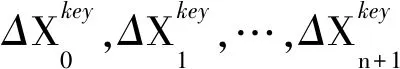
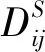

2.2 局部路径修正

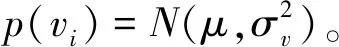

3 回放式仿真试验







4 结论

