惯性系姿态确定的SINS晃动基座初始对准算法

周 月，曾建辉，刘 猛,2，马文霞，李慧芸

(1.哈尔滨工程大学自动化学院,哈尔滨 150001； 2.天津航海仪器研究所，天津 300131)

0 引言

当载体处于受到外界干扰(例如阵风，发动机待机和海浪等)的晃动基座初始对准时，载体的位置几乎不会发生变化，而其角运动可以近似看作是低频周期的摇摆运动，从而使得惯性测量单元(Inertial Measurement Unit，IMU)中陀螺仪输出的信噪比很低，故采用传统解析粗对准算法将无法完成捷联惯导系统(Strapdown Inertial Navigation System，SINS)的初始对准过程[1-2]。由于其抗干扰能力较弱，传统解析粗对准方法通常仅适用于静基座初始对准。为了解决传统解析粗对准无法完成的SINS晃动基座初始对准，在2000年，Gaiffe和Cottrea提出了惯性系下观测重力视运动的初始对准思路，并应用在了法国iXSea公司的Octans光纤罗经中[3]。然而由于商业利益和技术安全，其详细实现过程未对外进行公布，仅仅提到了通过观测重力矢量在惯性系的视运动。对于重力视运动，如图1所示，即随着地球自转，重力在惯性坐标系内做锥形运动，运动周期为地球自转周期[4]。

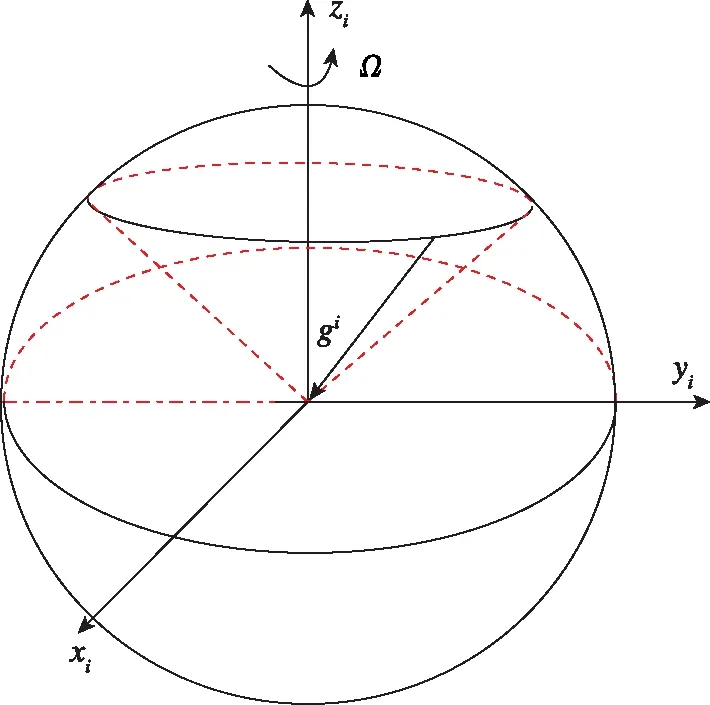
图1 重力矢量的视运动Fig.1 Apparent motion of local gravity vector

另一方面，在实施惯性系姿态确定初始对准过程中，传统惯性系姿态确定初始对准算法通常采用直接构造重力矢量观测来实现初始对准过程。然而由于在晃动基座自对准过程中不可避免存在的线运动误差以及近似化误差，将会引起矢量构造共线，从而造成初始对准过程姿态计算震荡，降低其对准性能[12-14]。

本文首先介绍了基于Davenport-q递归算法的惯性系姿态确定初始对准过程的基本原理。然后，对基于重力矢量观测的姿态确定初始对准算法在执行晃动基座对准过程中存在的问题进行分析。同时，通过分析晃动基座初始对准实际条件，提出了采用构造速度矢量观测来实现SINS姿态确定初始对准过程，则可以充分利用积分平滑作用，抑制周期性噪声和高斯白噪声，从而提高其对准性能。最后，通过千岛湖码头系泊状态的SINS初始对准对比试验对其进行了验证分析。

1 惯性系姿态确定初始对准算法

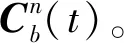
(1)

式中，b(0)和n(0)分别为初始零时刻的载体坐标系和导航坐标系，其不随时间旋转且相对于惯性空间(i系)静止，从而为惯性系，并称为凝固惯性系；b(t)和n(t)分别为t时刻的载体坐标系和导航坐标系。

(2)

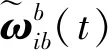
(3)

根据坐标转换关系，易有

(4)

将式(1)代入式(4)可得

(5)

(6)

令

(7)

(8)

则式(6)可以重写为

(9)

(10)

(11)

式中，M代表矢量观测的数量；αi和βi分别为式(7)和式(8)的离散形式。

进而，式(10)的递归计算形式也可以给出为

(12)

(13)

2 SINS晃动基座初始对准

当载体在晃动基座进行对准时，对式(8)中的fn进行计算，根据惯导系统的比力方程可知

(14)

对式(6)两边在相同的时间区间内进行积分得

(15)

从而构造惯性系速度矢量观测为

(16)

(17)

根据周期特性，则有

(18)

由式(18)可知，SINS晃动基座自对准过程中存在的忽略近似项，由于其具有周期特性，即使被忽略掉，也可以通过积分构造速度矢量观测减小其对初始对准过程的影响，从而提高晃动基座初始对准的性能，则式(17)可以重写为

(19)

3 千岛湖系泊测试试验

图3 船舰和IMU设备Fig.3 Ship and IMU equipment

图4 基于重力矢量观测的SINS姿态确定初始对准过程中的姿态计算结果Fig.4 Results of attitude calculation in the process of SINS initial alignment with attitude-determination algorithm based on gravity vector observation

图5 基于重力矢量观测的SINS姿态确定初始对准误差曲线Fig.5 The curves of alignment error with attitude-determination algorithm based on gravity vector observation for SINS

图6 基于速度矢量观测的SINS姿态确定初始对准过程中的姿态计算结果Fig.6 Results of attitude calculation in the process of SINS initial alignment with attitude-determination algorithm based on velocity vector observation

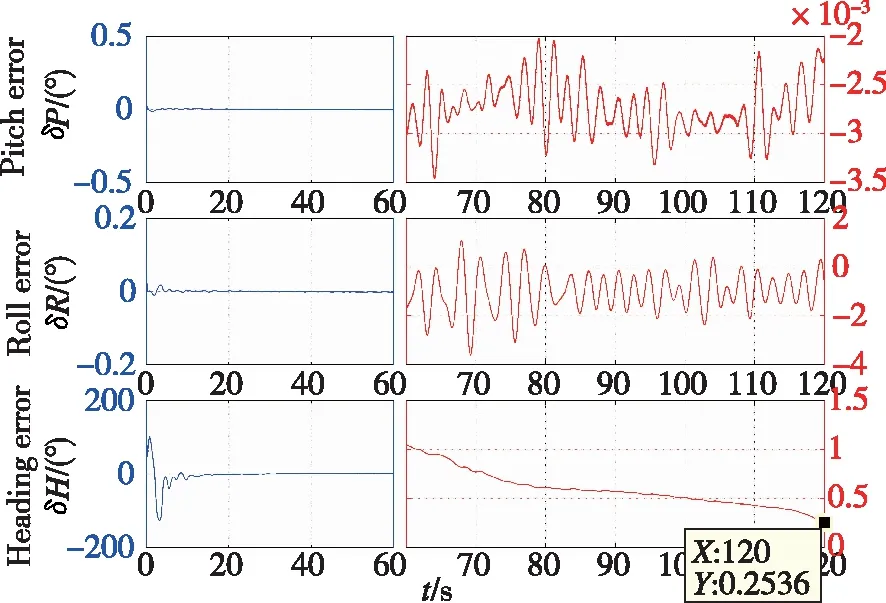
图7 基于速度矢量观测的SINS姿态确定初始对准误差曲线Fig.7 Curves of alignment error with attitude-determination algorithm based on velocity vector observation for SINS

由图5和图7可知，惯导系统的三轴对准误差随时间逐渐收敛于0，故SINS惯性系姿态确定初始对准算法可以解决传统解析粗对准在晃动基座以及受到外部干扰时所面临的初始对准问题。另外，由图4和图6可知，采用Davenport-q递归算法完成SINS惯性系姿态确定初始对准过程中，可以实时得到载体的姿态，从而相对于传统的双矢量求解算法仅可以在对准结束时得到载体的姿态矩阵，其可以充分利用观测信息，具有更优越的性能。

此外，通过对比图4和图6以及图5和图7易知，采用重力矢量观测完成SINS晃动基座姿态确定初始对准过程，其航向对准一直存在着震荡。但基于速度观测矢量完成SINS姿态确定初始对准的误差曲线更加平滑，具有更高的对准精度。这是因为在晃动基座姿态确定初始对准过程中，重力矢量观测构造中无法避免的近似过程以及测量噪声会造成观测矢量的共线，进而引起初始对准过程的震荡，从而降低SINS对准性能。而通过构造速度矢量观测来完成的SINS晃动基座姿态确定初始对准时，其可以有效地利用积分平滑作用，进而弱化近似化过程的影响并抑制外部扰动误差的干扰。同时在120s对准结束后，两种算法的航向对准误差分别为-0.4299°和0.2536°。因此，采用速度矢量观测构造的惯性系姿态确定算法将更具优越性能。

4 结论

1)SINS惯性系姿态确定初始对准通过矩阵分解，则可以有效地隔离由外部干扰对初始对准性能的影响。为了充分利用其每一时刻的观测信息，采用Davenport-q递归算法来求解其常值姿态矩阵，则可以实时求得SINS的姿态矩阵，从而具有优越的性能。

2)针对传统直接构造重力矢量观测的姿态确定初始对准算法在执行晃动基座对准过程中所存在的问题，通过分析晃动基座初始对准实际条件，提出了采用构造速度矢量观测来实现SINS姿态确定初始对准过程，可以充分利用积分平滑作用，抑制周期性噪声和高斯白噪声，从而可以提高其对准性能。

3)通过千岛湖码头系泊状态的SINS初始对准对比试验对其进行验证。通过构造惯性系速度矢量观测来实现SINS姿态确定初始对准算法，可以充分利用积分平滑作用，抑制外部扰动误差的干扰，从而具有更优越的性能。