透过现象背后的本质究竟在哪里

刘华为

【摘 要】透过现象看本质是教师研究教材、教法与学法的必备技能，而透过现象挖掘出什么样的本质与教师的专业基础、教学经验和剖析角度密不可分。这需要教师平时多阅读、多反思、多积累，以完善认知方式，丰富教学策略，提升研学能力，进而提高自己透过现象挖掘本质的科学性与综合性能力。

【关键词】透过现象看本质;内角和定理;辅助线

笔者拜读了孟莹和张昆两位老师发表在《中小学课堂教学研究》杂志2019年第7期的《三角形内角和定理教学设计的新视角——透过培养“数学辩证思维”的视点》（以下简称文[1]）一文后深受启发，懂得了如何透过现象挖掘本质，并依据本质内涵设计突出知识生成过程的探究性教学，以激发学生的学习兴趣，培养其数学辩证思维。但对文[1]关于“三角形内角和定理”的教学设计和部分观点，笔者也有一些不同的想法，与大家共同探讨。

一、问题回顾

文[1]认为，常规方法是运用图1（过点A作直线DE∥BC）与图2（延长BC至点D，过点C作CE∥AB）两种添辅助线的做法来证明三角形的内角和为180°，均存在一定弊端。因为辅助线是“无中生有”画出来的，是借助“操作与观察”由教师告知的，不是学生“探究发现的结果”，因而学生“只知其然而不知其所以然”。鉴于此，文[1]对该定理教学进行了如下“二次开发”。

第一步：由两副直角三角尺三个内角度数之和，得出特殊直角三角形的内角和为180°。

第二步：以“是否所有的直角三角形内角和都是180°？理由是什么？”问题，引导学生通过添加如图3的辅助线（过点A作AD∥CB）加以证明（具体过程请参阅文[1]，下同）。

第三步：由直角三角形内角和为180°推广到一般三角形，并通过作三角形一边BC上的高AD（如图4）构造直角三角形进行证明。

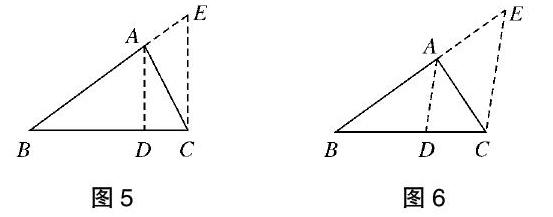
第四步：通过在△ABC外构造Rt△BCE（如图5），再让点D在边BC上动起来，进行一般化处理，得到图6的辅助线证法。特别地，当点D与点B重合时，得到图2的辅助线添法。

从表象来看，上述设计确实给人耳目一新之感，由特殊的直角三角形入手，引导学生经历猜想、验证与探索的过程，使辅助线的生成自然流畅、层层递进，环环相扣，突出了从特殊到一般的转化过程，似乎揭开了辅助线生成与问题解决的本源。可笔者认为有一些地方还是值得探讨的。

二、启发之处

1.关于教学设计

其一，正如文[1]所说，学生在四年级已经经历度量或拼图操作，验证了三角形的内角和为180°。换言之，学生早已知晓三角形的内角和为180°，那么文[1]让学生由两副直角三角尺的内角和为180°猜想直角三角形的内角和也为180°，是否有明知故问之嫌？

其二，如果说图1和图2的辅助线是“无中生有”画出来的，那么在图3中又怎么想到过点A作BC的平行线AD呢？是否有强加之意？倘若把辅助线的作法表述为“过点A作AC的垂线DA”或许还可以解释，因为要得到180°，既然∠C=90°，那么再构造一个直角也就顺理成章了。当然，单从知识转化角度切入，图3的辅助线生成也有合理生成之处，因为要得到180°，自然会想到“两直线同旁内角互补”，进而过点A作AD∥BC。只是如此一来，过△ABC任一顶点作其对边的平行线皆可直接证明。更何况，笔者认为文[1]也没能透过现象发现“知识转化”这一本质。

其三，图3的辅助线一旦生成，从方法迁移角度而言，对于非Rt△ABC作出图7的辅助线（其中AD∥BC）岂不更加自然流畅？何必舍近求远地借助图4、图5、图6绕一大圈呢？当然如果到图4为止也无可厚非，因为把一般三角形转化成刚证明的直角三角形来处理也是水到渠成。可是文[1]为了凸显图2辅助线的生成“本质”，强行借助图5与图6过渡，笔者认为有过度开发之嫌。在△ABC外构造Rt△BCE，再作BC邊上的高（如图5），然后让点D动起来（如图6），即作一般化处理，再借助点D与点B重合而得到图2的辅助线，恐怕是学生的能力难以达到的。

2.关于辅助线的添加

其实，小学撕角拼图的操作（如图8）除了验证三角形的内角和为180°，还突出了转化思想，即要证明三角形的内角和定理，只需利用图形的等量变换（平移、翻折与旋转）把三角形三个内角转化为度数为180°的平角，这就是图1和图2辅助线的生成点。显然，图1就是把∠B绕AB中点旋转180°到∠BAD位置，∠C则是绕AC中点旋转180°到∠CAE位置，此时AD∥BC且AE∥BC，而由“过直线外一点有且只有一条直线与已知直线平行”得AD与AE共线，故“过点A作DE∥BC”的辅助线添法应运而生。当然，图2 的辅助线生成就是把∠B向右平移至∠DCE位置（或把∠A绕AC中点旋转180°至∠ACE位置）。由此可见，图1与图2的辅助线并非“无中生有”。

3.关于辅助线的生成点

表面上看，图1与图2的辅助线生成是受小学拼角的启发，但透过现象看本质，其实不借拼图，依然可以挖掘出辅助线的生成点。众所周知，从转化思想来看，所有数学问题都是运用所学过的知识加以解决的。因此，欲证三角形的内角和为180°，则之前学过的与180°有关的知识源“平角的意义（含邻补角）”与“两直线平行同旁内角互补”才是解决问题的方向。若用知识源“平角的意义”处理，借助图形的等量变换便可得图1与图2的两种证法;若用知识源“两直线平行同旁内角互补”处理，则易得图7的辅助线构造方法。由此可见，与180°有关的两大知识源才是证明三角形内角和定理时所添辅助线的生成点。

值得指出的是，构造平角证明三角形内角和定理时，所构造平角的顶点可以是△ABC所在平面内任意一点（如图9）。有的教师喜欢把平角顶点O放在△ABC的顶点、边上、三角形内与三角形外逐一证明，其实意义不大，因为这些方法都是统一的（即构造平角来处理），只是选点位置不同或过程表述稍有差异而已。

综上所述，文[1]的新颖设计虽然凸显了从特殊到一般的认知规律，笔者却觉得未能抓住现象背后的本质。

三、设计建议

鉴于以上分析，笔者觉得关于三角形内角和定理的教学不必过多纠结，不妨借助下列驱动问题引导学生学会思考和转化。

问题1：在小学我们就知道三角形的内角和为180°，请问是怎么得到的？（度量和拼图）

问题2：限于认知水平不同，小学只需验证即可，但到了初中一定要进行严格的推理证明，那么如何证明呢？（若学生难以回答，教师可作如问题3的引导）

问题3：一般地，数学问题都是运用学过的知识来解决。那么，我们学过的与180°有关的知识点有哪些？（“平角的意义”和“两直线平行同旁内角互补”）

至此，过三角形某一顶点作其对边的平行线（如图7），运用“两直线平行同旁内角互补”来证明“三角形内角和定理”已是水到渠成;而如何运用“平角的意义”来证明还需教师做进一步的启发。

问题4：如何运用“平角的意义”来证明三角形内角和定理呢？小学的拼图给你什么样的启发？（把三角形三个内角等量转化到同一平角内）

问题5：如何进行角的等量转化？（教师可从角的位置变化引出图形变换，从而得出“平移、翻折和旋转”）

运用转化思想来驱动问题解决的最大益处是让学生学会如何思考，这不仅让学生知道怎么做，更知道为什么这样做，从而有效地突出学法指导，强化解决问题的能力。

四、总结反思

透过问题现象看本质虽然不是当下的热门话题，却是一个经典话题，而且对提升教师的专业素养有着深远的影响。那么，透过现象如何挖掘本质或者挖掘什么样的本质呢？

1.透过众多“发现”现象厘清认知规律的本质

关于三角形内角和定理的发现，不少研究者进行了教学设计，比较典型的有以下三种。

设计一：在图10中，不妨设BC为△ABC最长的边，分别在BC、CB延长线上各取一点N、M。借助几何画板动态演示，首先把直线MN绕点B按逆时针方向旋转至∠ABC的度数，则点N在BA的延长线上且点M在AB的延长线上;再把旋转后的直线MN绕点A按逆时针方向旋转至∠BAC的度数，则点N在CA的延长线上且点M在AC的延长线上;最后把刚旋转所得的直线MN绕点C按逆时针方向旋转至∠ACB的度数，则点N在CB或CB的延长线上且点M在BC的延长线上。此时可以发现直线MN正好被旋转了180°，由此得三次旋转角之和（即三角形的内角和）等于180°。

此设计新颖独特，动态感强，更能与现代化的多媒体技术相融合。但显然比较晦涩难懂，有违深入浅出之教學设计原则，更何况本设计对定理的证明没有任何启发之处，只是为了发现而“发现”，似乎有过度设计之嫌。

设计二：如图11，有的教师借助几何画板动态演示，当点A无限趋近于点O时，可发现△ABC的内角和接近于平角，从而猜想三角形的内角和为180°。还有的教师用自制的橡皮筋道具演示（橡皮筋起初与边BC重合，然后从点O处沿OA拉到点A处放开），也很生动形象。

本设计只说明了三角形的内角和趋近于180°，并未能对定理做出证明。

设计三：如图12，当点C沿着射线BC向无穷远处运动时，∠ACB越来越小，越来越接近于0°，而∠BAC越来越大，越来越接近于∠BAD。特别地，当AC与BC没有交点（即AC与AD重合）时，和为180°，进而猜想三角形的内角和为180°。

该设计的优越性在于把辅助线AD显性化了，是上述三种设计中较为成熟的操作方法，但难免有“事后诸葛亮”之嫌。

应当指出的是，在设计二上点A与设计三上的点C运动时，有的教师默认变化中的△ABC内角和总是相等的（即每个变化后的三角形内角和都相等，从而依据终极图形得到三角形的内角为180°）。这显然不妥，因为在没有证明三角形内角和定理前，还不知道三角形的内角和是个定值。换言之，当点A（或点C）运动时，△ABC的内角和是不变或变大或变小或忽大忽小都是未知的，只能说明两种设计的结果都验证了三角形的内角和趋近于180°，进而得出猜想。

其实，透过各种纷杂的精彩设计，笔者觉得从小学的“度量计算猜想”和“撕角拼图验证” 到中学的“作平行线推理证明”最契合学生的认知水平与认知规律，既通俗易懂又便于操作，而且融定理的发现与证明为一体。

2.透过众多证法现象厘清转化思想的本质

正如前文指出，有的教师把图9中的点O设置在△ABC的某条边上，或边的延长线上，或三角形内，或三角形外，然后在课堂上引导学生逐一证明。其实，这就是没有厘清转化思想（即把三角形的三个内角通过图形变换转化为平角处理）的本质，只是追求形式上的创新，而忽视对学生转化与迁移能力的培养。文[1]的设计虽然体现了从特殊到一般或化一般为特殊的转化思想，但只涉及转化思想之形，并未厘清转化思想之本质，因为对“所有数学问题都是运用所学过的知识加以解决的”理解不透，从而导致未能从知识源入手，寻求解决问题的突破口，也使整个教学设计走了不必要的弯路。

总之，只有从探求知识生长点、难点和学生能力发展点入手，对教材进行深度挖掘与理性思考，才能看清定理生成的本质、透过辅助线作法看清知识转化的本质、透过思路剖析看清学法指导的本质、透过思维训练看清能力发展的本质。进而设计出符合学生认知基础并遵循学生认知规律的教学流程，提升学生的发展性学力，全面落实核心素养。