HPM视角下的初中函数概念课例研究

秦语真 汪晓勤 余庆纯

【摘 要】函数概念是中学数学的核心概念。部分初中教师由于对函数概念的历史缺乏了解，掌握的有关史料有限，对数学史教育价值的理解不够到位，因而在实践中往往难以在教学中重构函数概念的发生和发展过程，难以让学生经历函数概念从“解析式说”到“变量依赖说”，再到“变量对应说”的自然发展过程，最终实现数学史的多元教育价值。研究者按照“聚焦与准备”“研讨与设计”“实施与评价”“整理与写作”的前三个环节，开展初中函数概念的课例研究。

【关键词】HPM;函数;重构

一、引言

函数概念是中学数学的核心概念。德国数学家F·克莱因（F.Klein）曾指出：“我确信函数概念的教学是学校的灵魂，以函数为中心，将全部数学教材集中在它的周围，进行充分的综合。”[1] 沪教版初中数学教科书采用函数的“变量依赖说”，而人教版教科书则采用了“变量对应说”。在有关研究者所呈现的函数HPM课例中，由于时间的限制，有的教师在课堂上未能实现从“变量依赖说”到“变量对应说”的跨越，也没有让学生感受到数学背后的理性精神，数学史应有的教育价值未能得到充分体现[2]。如何在教学中重构函数概念的发生和发展过程，让学生经历函数概念从“解析式说”到“变量依赖说”，再到“变量对应说”的自然发展过程，最终实现数学史的多元教育价值？部分初中教师由于对函数概念的历史缺乏了解，掌握的有关史料有限，对数学史教育价值的理解不够到位，因而在实践中往往难以有效地解决上述问题。

为此，HPM工作室按照“聚焦与准备”“研讨与设计”“实施与评价”“整理与写作”四个环节，开展了初中函数概念的课例研究。本文根据前三个环节，呈现函数概念的课例形成过程，以期为函数概念教学以及初中HPM课例研究提供参考。

二、聚焦与准备

（一）问题聚焦

函数概念历史发展过程中的障碍也会成为今天学生学习函数概念的认知障碍[3]。据有关调查研究表明，初中生对函数概念的理解倾向于“解析式”，他们对于表格和图像两种表达方式的理解存在困难[4]。针对已有HPM课例中的不足，借鉴其他教学研究的结果，本次课例研究将聚焦以下问题。

如何借鉴历史，从学生的认知起点出发，让他们经历函数概念的发生和发展过程？

如何实现数学史的多元教育价值？

（二）史料搜集

确定要解决的问题后，高校研究者对函数概念的历史进行了梳理。

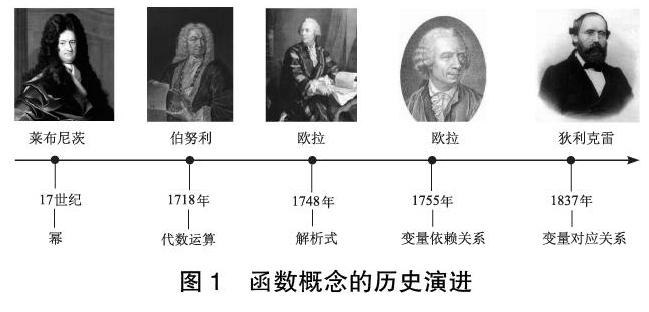
早期函数的概念经历了从17世纪莱布尼茨（G.W.Leibniz）眼中的“幂”到18世纪伯努利（John Bernoulli）定义的“代数运算”，再到18世纪欧拉（L.Euler）定义的“解析式”和“变量依赖关系”，最后到19世纪狄利克雷（P.G.L.Dirichlet）定义的“变量对应关系”[5]1-7（如图1）。

最初，莱布尼茨认为函数指的是x的幂，但接下来莱布尼茨将曲线上某一点的横坐标、纵坐标、切线长、次切线长、法线长以及次法线长这六个几何量称为函数[6]。要表达与幂函数图像对应的六个几何量，需要对幂实施代数运算，因而导致函数概念从幂到代数式的演进。1718年，瑞士数学家伯努利（John Bernoulli）將一个变量的函数定义为“由该变量和常数以任何方式组成的量”[7]。

1748年，瑞士数学家欧拉（L.Euler）在《无穷分析引论》中进一步将一个变量的函数定义为“由该变量和一些数或常量以任何方式组成的解析表达式”[5]1-7。但欧拉所说的表达式已包括指数函数这样的超越函数，从而突破了代数式的局限性。

随着“弦振动问题”的出现，函数概念再一次引发了数学家们的思考：把一根两端固定的弹性弦形变成某种初始状态，如何刻画振动弦在某时刻的函数[8]？这个图像可以由一个具体的解析式给出吗？一般地，一条徒手画出的任意曲线有解析式吗？面对这样的问题，欧拉在《微分基础》中更新了函数定义：“如果某些量依赖于另一些量，当后面这些量变化的时候，前面这些变量也随之变化，则前面的量称为后面的量的函数。”[5]1-7这就是我们通常所说的“变量依赖说”，沪教版初中数学教科书中的定义与此相似，只不过局限于一元函数。

但新的问题又产生了。若在x的某个变化范围内，y始终取常数值，此时y是否是x的函数？仅仅根据“变量依赖说”，是无法回答上述问题的。1837年，德国数学家狄利克雷（G.L.Dirichlet）进一步扩展了函数概念：“如果对于给定区间上的每一个x的值有唯一的y值和它对应，那么y就是x的一个函数。”[9]这就是我们通常所说的“变量对应说”。该定义被称为函数的现代定义，是函数概念认识上的一次飞跃。人教版初中数学教科书中的定义与此相似。

尽管狄利克雷给出了函数的现代定义，但人们并没有因此抛弃“解析式说”或“变量依赖说”，毕竟这两种定义更容易被人理解。19世纪，英国数学家德摩根（A.De Morgan）在《代数学》，以及美国数学家罗密士（E.Loomis）在《代微积拾级》中都仍然采用函数的“解析式说”。中国数学家李善兰和英国传教士伟烈亚力（A.Wylie）在翻译这两部著作时，将“变量”译为“变数”，将“包含变数的表达式”译成“函数”，其中“函”“含”同义[5]1-7。从此，“函数”一词在我国一直沿用至今。

（三） 初步设计

HPM工作室为执教者提供了有关函数概念的史料和国内已有的函数概念教学设计。执教者在研读相关材料之后，结合教材和学情分析，拟订了如下教学目标。

（1）通过具体实例，让学生认识变量和常量。

（2）知道用运动、变化的观点看待事物，理解在变化过程中，两个变量之间相互依赖的含义，从而理解函数的概念;知道函数的自变量以及函数解析式。

（3）在合作交流中，激发学生学习的积极性，培养学生迁移类推和概括的能力。

（4）通过对函数概念的产生、发展以及引入中国的过程的了解，加深对函数概念的理解，并感受数学文化的魅力。

以下是执教者初步的教学设计（见表1）。

三、 研讨与设计

（一）历史分析

根据函数概念的历史，可以得到以下教学启示。

为了让学生实现从“代数式”到“变量依赖关系”的过渡，需要他们认识那些无法写出解析式或从图像上看没有规律的函数。两个变量之间只要存在“依赖关系”，其中的一个变量就是另一个变量的函数。

为了呈现函数认识的历史相似性，教师需要创造机会，让学生了解历史上莱布尼茨、伯努利、欧拉、狄利克雷等数学家对函数的不同理解。通过微视频，让学生认识函数概念的演进过程，感受数学家的理性精神。

（二）交流研讨

根据历史启示、教学目标和本次课例研究所聚焦的问题，工作室成员与大学研究者针对教学设计1展开了交流和研讨。在研讨中，大家形成以下意见。

（1）问题设计层次不够鲜明，衔接不够流畅，未能有效呈现函数概念自然发生和发展的过程。

（2）在概念形成环节，缺乏对函数定义的解读和辨析过程。

（3）问题不够贴近初中生的生活经验。

（4）数学史的运用方式过于单一，仅有附加式，因而其教育价值不够多元。

（5）播放两段微视频和一则阅读材料，不切合课堂实际，需要合并。

（6）微视频2“函数概念的发展简史”过于学术化，内容比较枯燥，不符合学生的认知规律。

（三）改进设计

根据研讨结果和历史启示，执教者对教学目标作了修正，将原有教学目标（4）改为 “了解函数概念的发展历程，加深对函数概念的理解，进而感受数学文化的魅力”，并从以下几方面对教学设计1做了改进。

在新课探究环节，以学校附近的滴水湖为背景，从表格的角度去研究路程与时间或速度与时间的关系，又以篮球为例，从图像角度研究位置与时间的关系。

删去微视频1和阅读材料。

在概念形成环节，增加了对函数定义中关键词的分析。

将微视频2的内容改为虚拟的“函数博物馆”。

增加数学写作的课后作业。

执教者最终形成的教学设计如下（见表2）。

从表2可以看出，执教者采纳了研讨活动中形成的意见（2）（3）（5）和（6），并做了相应的修正。然而，修正的教学设计并未解决意见（1）和（4）所涉及的问题。

四、实施与评价

（一）第一次教学

执教者按照教学设计2进行了第一次教学。教学前后，对授课班级的学生进行了测试。结果表明，学生对于“图像不规则或不连续、无法写出具体解析式的变量关系也可以是函数”这一事实印象深刻;学生对于微视频“函数博物馆”非常感兴趣，认为了解数学家对函数的认识，就像“和他们对话一样”。

从课后测试结果来看，不少学生对于变量之间的对应关系存在误解，有7名学生虽认为x的一个值只能对应于y的唯一一个值，但同时又认为y的一个值也只能对应于x的唯一一个值。

在研究表格中的对应关系时，有24.2 的学生认为只有能写出解析式的对应关系才是函数;在研究函数的图像依赖关系时，有30.3 的学生认为没有规律的图像所表示的并不是函数。

执教者针对第一次教学进行了反思，认为本节课存在以下几个问题。

（1）由例题直接过渡到函数概念的过程不够自然，学生不能很好理解函数概念;

（2）微视频对于学生理解函数概念的作用不大;

（3）学生不能很好地将表格和图像与函数的定义相结合;

（4）交流研讨中形成的意见（1）和意见（4）并未得到解决。

（二） 第二次教学

根据第一次教学的反馈和反思，执教者对教学目标做了进一步修正，将（1）改为“掌握变量与常量的概念”;在（2）中增加“经历函数概念的形成过程”;删去（3）“在合作交流中，激发学生学习的积极性，培养学生迁移类推和概括的能力”。执教者还对教学设计2做了以下改进。 在课堂中，绘制一些“形状奇怪”“没有规律”的图像，帮助学生理解函数定义。

执教者根据以上改进，最终形成教学设计3。从教学设计3可以看出，执教者根据自己对第一次教学的反思，对教学设计2做了相应的改进。针对研讨活动中形成的意见（1）和意见（4），通过将学生对于函数认识与历史上数学家的定义进行对照，在一定程度上让学生经历了函数概念的演进过程，但问题之间的衔接依然不够流畅，数学史的价值（如德育价值）体现得仍不够充分。

按照教学设计3，执教者实施了第二次教学，课后对教学进行了深刻的反思，从以下几方面对教学设计3做出改进（见表3）。

（三）第三次教学

根据第二次教学的反馈和反思，执教者对教学设计3做了进一步修正，形成教学设计4（见表4）。

按照教学设计4，执教者实施了第三次教学。在新课探究环节，将画面转到滴水湖，探究速度、时间和路程之间的关系，完善学生对常量和变量的认识，使衔接更为自然。在概念形成环节，执教者首先展示全班学生的课前测试结果，并告诉学生，数学家对于函数的认识也是不尽相同的。然后，执教者播放微视頻，依次给出历史上数学家对函数的不同定义。最后，执教者在黑板上依次画出与历史上函数定义相对应的图像，让学生体会函数定义不断演进的过程（如图2）。

教师将学生课前测试中对函数概念的认识与数学家的函数定义对应起来：“一种运算方式”“代数式”和伯努利的定义相似;“图像”“解析式”与欧拉的第一个定义相仿; “常值函数”恰好符合狄利克雷的定义。教师通过古今对照，让学生了解函数概念，经历从“解析式”到“变量依赖关系”，再到“变量对应关系”的过程。

（四）学生反馈

第三次教学之后，执教者从认知和情感两个维度对授课班级的40名学生进行了课前测试和课后测试。结果表明，课前学生对函数概念的理解大都局限于具体的正比例函数、反比例函数以及解析式;而课后学生普遍达到“依赖关系”和“对应关系”的水平。关于表格中的“变量对应关系”，课前学生的正确率是20 ，课后正确率达到了85 。关于图像中的“依赖关系”，课前学生的正确率是12.5 ，而课后正确率达到了95 。关于图像中的“对应关系”，课前学生的正确率是17.5 ，而课后正确率达到了97.5 。在图像为离散点的情形中，课前学生的正确率为5 ，课后正确率达到了 97.5 ，说明学生从表格和图像方面对函数概念有了较好的理解。

课后测试卷增加了两个问题，第一个问题是让学生说一说对本节课中印象最深刻的内容。22名学生提到“函数博物馆”微视频，他们认为通过微视频，可以与数学家进行思想碰撞;明白数学是要经过不断推敲而得到的;函数定义不断演进的过程符合他们的认知规律。有的学生还提出：“如果处于那个时代，我们也会有这样的发现”;“时代造英雄，时代不断推动数学向前发展”。有12名学生原以为“连续的”“好看的”“有规律的”才是函数，是函数定义颠覆了他们以前的认识。

第二个问题是让学生根据数学史的六类价值来谈本节课的收获。关于知识之谐，学生认为从生活实例引入，再由解析式到图像，过程自然，将代数和几何联系在一起，使认识更加全面。关于探究之乐，学生认为他们提出的函数一定是连续的，一定具有规律，虽然后面都被否定了，但是他们经历了思考的过程，并探究了函数定义的关键词，明白了“确定的依赖关系”的内涵。关于方法之美，学生认为判断函数的方法十分简洁。关于能力之助，学生认为提高了数形结合和思辨的能力。关于文化之魅，学生通过“函数博物馆”的微视频，了解历史上数学家给出的函数定义，并感受历史相似性。关于德育之效，学生有了坚定的数学信念，认为生活中处处有数学，同时也认为数学概念是随着时代的发展而不断演进的，反映出动态的数学观。

（五）同行评议

第三次教学之后，工作室教师和高校研究者对本课进行了点评。与已有HPM教学设计相比，本节课做了颇多的创新。一是将课前测试结果与历史上数学家的函数定义进行对照;二是课后作业采取数学写作的形式，有助于及时捕捉学生的所思所想;三是突破了沪教版教材中的“变量依赖说”，引领学生跨越到“变量对应说”;四是播放微视频，并将函数概念的发展诸阶段用相应的图像展示出来。同时，执教者在课堂上鼓励学生说出自己对函数的理解，不断纠正他们不正确的认知，鼓励他们继续探索函数的定义，培育了学生的探究精神，渗透了数学学科德育。

同时，工作室教师指出本节课存在一定的难度，对学生的认知水平要求较高。执教者授课班级学生理解能力较好，将其放入其他层次的班级进行教学不具有推广性。

（六）教师反思

第三次教学之后，执教者对函数概念教学进行了以下反思。

1.将数学史融入数学课堂要自然。要让数学史为数学概念的讲解提供依托，使学生对于数学概念的理解过程更为自然。

2.教学形式应多样化。在课堂上播放微视频，吸引了学生的注意，而单一的板书讲解，很难让学生理解函数的抽象概念。

3.数学课堂应重视和生活之间的联系。要让学生感受到数学是有用的，而不是脱离生活实际的。将函数与生活中的路程、时间等问题结合，可以拉近函数概念和学生之间的距离。

4.数学是有德育价值的。教师要在数学课堂上让学生体会数学概念的严谨性以及数学家的理性精神，激励他们像数学家一样积极探究和思考，追求真、善、美。

五、结语

在本次课例研究中，函数概念的教学设计前后经过了三次改进和三次实施，所聚焦的问题基本上得到了解决：通过对学生的课前测试，寻找学生对于函数概念的认知起点;通过现实生活中的例子，呈现函数的“解析式”“变量依赖关系”和“变量对应关系”三种内涵;通过HPM微视频，展示了函数概念从“解析式”到“变量依赖关系”再到“变量对应关系”的演进过程;通过古今对照，让学生以“概念建构者”的身份经历函数概念的自然发展过程;函数概念的历史不仅帮助学生正确认识数学活动的本质，树立动态的数学观，而且让学生感悟数学背后的理性精神。美中不足的是，执教者未能采用重构式展开教学，在问题串的设计上仍有很大的改进空间。

从本次课例研究中，我们得到以下启示。

首先，HPM视角下的数学教学的基本特征之一是为学生提供探究机会，让他们经历知识的发生和发展过程，教师可以采用“古今对照”的策略，让学生“穿越时空与数学家对话”，既亲近数学，又加深对数学的理解。

其次，数学史的运用方式有附加式、复制式、顺应式和重构式，其中重构式是揭示知识发生和发展过程的最佳方式。在运用重构式时，教师首先需要把握有关主题历史发展的关键环节以及从一个环节到下一个环节的动因，然后设计一系列由易到难、层层递进的问题，再现主题的历史发展。

最后，数学史的“德育之效”，在教学中未必可以自然达成，需要教师明确的“点拨”。教师可以通过呈现历史相似性，提升学生的自信心;或让学生思考数学史对自己的思想启迪，感悟数学背后的理性精神。

参考文献：

[1]COONEY T J，WILSON M R.Teachers thinking about functions：historical and research perspectives [M].Hillsdale：Lawrence Erlbuam Association Publishers，1993.

[2]方倩，杨泓.HPM视角下的初中函数概念教学[J].中学数学月刊，2016（11）：40-43.

[3]任明俊，汪晓勤.中学生对函数概念的理解：历史相似性初探[J].数学教育学报，2007（4）：84-87.

[4]陈烨.针对初中函数学习困难的教学设计与实践[D].济南：山东师范大学，2013.

[5]汪晓勤.19世纪中叶以前的函数解析式定义[J].數学通报，2015 （5）：1-7.

[6]杜石然.函数概念的历史发展[J].数学通报，1961（6）：36-40.

[7]钟萍，汪晓勤.函数概念：基于历史相似性自然过渡[J].教育研究与评论（中学教育教学）， 2016（2）：62-68.

[8]刘思璐，汪晓勤，沈中宇.HPM视角下的高中函数概念课例研究[J].中小学数学（高中版），2019（1/2）：37-41.

[9]黄深洵，刘思璐，沈中宇.HPM视角下的函数概念教学[J].中学数学月刊，2019（9）：53-56.