多信息观察置信定价下的连续内部交易最优策略研究

张 亮，周永辉

(1.贵州师范大学 数学科学学院，贵州 贵阳 550025；2.贵州师范大学 大数据与计算机科学学院，贵州 贵阳 550025)

0 引言

1985年，Kyle[1]描述了一种内部交易市场，内部交易者利用拥有的私有信息，以噪声交易者为掩护，选择交易策略使利益最大化。同时，证明了这种动态内部交易市场在做市商进行半强有效性定价下的线性均衡的存在性，并讨论了均衡时信息释放和市场的特征。而Jain和Mirman[2]建立了做市商收集到交易总量和部分风险资产价值信息的内部交易模型。Luo[3]还研究了做市商和内部交易者同时知晓部分风险资产价值信息的内部交易模型。其他关于离散型内部交易研究，见文献[4-12]。

1992年，Back[13]将Kyle[1]的离散内部交易模型推广到连续内部交易模型。然后，Back和Pedersen[14]对内部人的高斯信息过程和高斯噪声交易过程进行了研究，得到了内部人的最优交易策略和对应的定价公式。Danilov[15]应用变式的Kalman-Bucy滤波和信息域流扩展方法，研究了一类服从扩散随机过程而其漂移项不确定的风险资产内部交易情形。Caldentey R[16]建立了一种将随机公告时间与接收信息流的内部人相结合的模型。Aase[17]应用滤波统计的方法，求出了一类单个内部交易者的连续内部交易的平衡策略。同年，Biagini[18]又研究了带记忆性噪声交易信息的内部交易特征。Collin-Dufresne[19]将Kyle-Back模型扩展到噪声交易波动性会随时间随机变化的情形。周[20]进一步研究了部分风险资产价值信息下的连续内部交易的线性策略均衡问题。段晶花[21]研究了连续内部交易市场中风险资产的价值扭曲和过度自信的现象。Ma[22]进一步得到了一类服从条件随机微分方程的风险资产信息下的连续时间内部交易特征，并得到一类新的随机微分方程弱适定性条件。胡[23]研究了一类偏离半强有效性定价下的连续内部交易。其他关于连续内部交易的研究进展，见最近综述性论文[24]。

在现实金融市场中，做市商往往会观察到关于风险资产的多种信息，而这些不同的信息将是否影响对风险资产的定价，是值得探讨的问题。本文将在以往文献的基础上，进一步研究当做市商观察到多种风险资产线性结构信息时，内部人如何在连续内部交易时进行最优决策，及其这些信息对最优决策的影响。

1 模型

本文所涉及到的随机变量和随机过程均定义在滤子化概率空间 (Ω,F,{Ft}t≥0,P)。

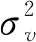
市场中有三类拥有不同信息的交易者：

1)内部人：知道风险资产v的真实价值，并且在t∈[0,T)时刻提交交易量xt；

2)噪声交易者：不知道关于该资产的任何相关信息，只能随机的进行交易，在t∈[0,T)时刻提交交易量：

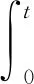
(1)

其中σzs>0是确定的连续可微函数，Bzs是标准布朗运动；

3)做市商：在t时刻,不但观察到总的交易量：

yt=xt+zt

(2)

而且观察到关于风险资产v的多种信息，为方便计，不妨观察到两种信息ut和nt：

ut=f(v,ε)

nt=g(v,η)

其中f,g是关于v和噪声项ε,η的确定Borel可测函数。

对于上述信息ut和nt，做市商如果不能直接判别谁更有效，那么做市商将以概率ρ相信ut，以1-ρ相信nt。这里ρ称为置信程度，ρ∈(0,1)称为非平凡置信程度。如果做市商能判断某一信息为无效信息时，对此信息赋予的置信程度为0，如果能通过某一信息直接推知风险资产真实价值，那么对此信息赋予的置信程度为1。

为了便于计算,我们做如下假设：

1)信息ut和nt是线性的，且噪声项是服从正态分布的。参照文献[20]对信息作如下处理,即：

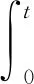
(3)

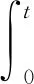
(4)

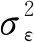
2)随机变量v，ε，η，Bzs，Bus，Bns是相互独立的；

3)内部人的交易策略[17]：

dxt=βt(v-pt)dt

(5)

其中βt称为内部人的交易强度，βt是[0,T)上的连续可微函数。

这样，内部人的财富[13]：

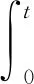
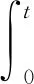
对应的期望财富：

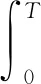
对于内部人而言，其目标就是找到最优交易强度βt，使得期望财富最大：

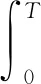
(6)

2 滤波方法

由方程(1)(2)(3)(4)(5)，总交易量过程和风险资产部分信息过程可写为以下向量方程：

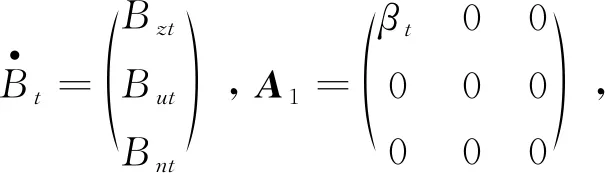
为了解决问题(6)，首先，我们考虑一个线性滤波系统：

(7)

由定义，更新过程为：

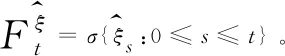
证明相关证明过程与文献[17]中证明过程类似，在此不再赘述。

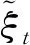
证明相关证明过程与文献[17]中证明过程类似，在此不再赘述。

为了便于表达，记

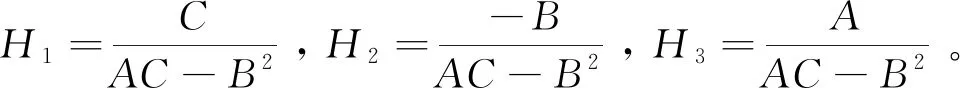
其中

证明对∀t∈[0,T]，则由文[25]的定理13.1有：

其中A+表示A的伪逆矩阵，AT表示A的转置。

v、ε和η相互独立

由定理12.8[25]有：

3 主要结果

在金融市场中，做市商观察到的信息可能会影响做市商的定价，内部人会根据市场的变化而改变自己的交易策略，以求累积到最多的财富。

定理1

1)当ρ∈(0，1)，AC-B2=0时，

(a)若k1=k2=0(或k3=k4=0)，则内部人的最优交易策略为

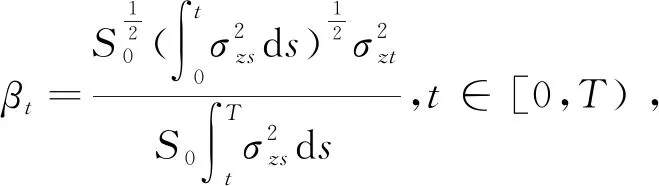
(b) 若k2=k4=0，则内部人的最优交易策略βt=0，t∈[0,T)，对应的期望财富J(βt)=0；

2)当ρ∈(0，1)，AC-B2≠0时，内部人的最优交易策略为

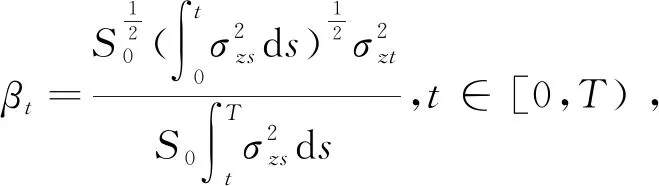
(k3v+k4η-k3E[v])

证明

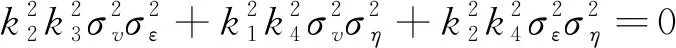
由假定，ki(i=1,2,3,4)不全为0，从而k2k3=0，k1k4=0且k2k4=0

要使得上述三个等式都成立，有且只有如下情况

(a)k1=k2=0(或k3=k4=0)，此时，无部分风险资产信息ut，由文献[21]可知内部人的最优交易策略为

(b)k2=k4=0，此时，无噪声项ε,η，做市商可由线性结构信息推知风险资产v的真实价值，所以内部人的最优交易策略为βt=0，对应的期望财富为J(βt)=0；

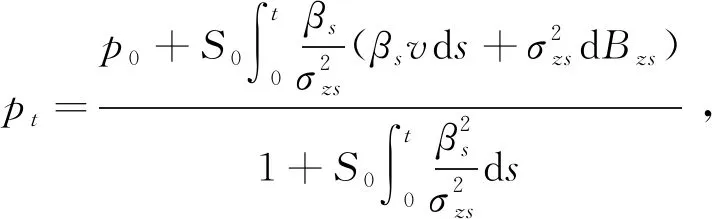
其中

类似文献[17]定理2.1的证明，即可得证内部人的最优交易策略为

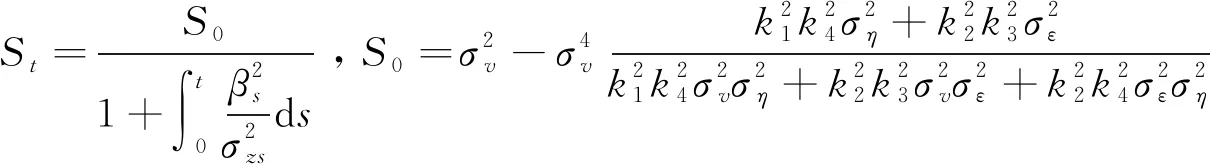
特别地：ST=0，可推出v=pTa.s.

4 性质

根据定理1，我们发现：

1)当ρ∈(0，1)，内部人的最优策略与最大期望财富不会随着做市商非置信程度的改变而改变；当ρ=0或ρ=1，表明内部人只相信某一信息，此时，与文献[21]情形相同，内部人的最优交易策略与最大期望财富见文献[21]；

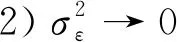
3)多信息过程ut,nt的扭曲系数ki∈R(i=1,2,3,4)共16种情形。对应的内部人最优策略和最大期望财富如下：

表1 多信息置信定价下的内部人最优交易策略与最大期望财富Tab.1 Insider’s Optimal Trading Strategy and Maximum Expected Wealth under Multi-information Confidence Pricing

注：由于信息ut，nt是具有相同线性结构的信息，所以其余6种对称情形在表中不予给出。

5 结论

本文对一类做市商对风险资产有多种信息观察的连续内部交易进行了研究，得到了内部人的最优交易策略与交易财富，而最优交易策略与做市商对信息的非平凡置信程度无关。多信息观察包含了无部分风险资产信息观察、单信息观察，且与之前相关研究结果保持一致。