一个部分盲签名方案的分析与改进

蒋雨宏，邓伦治

(贵州师范大学 数学科学学院，贵州 贵阳 550025)

0 引言

1984年Shamir[1]提出的基于身份密码体制，简化了密钥管理过程，避开了证书的管理问题，解决了传统公钥密码体制的缺陷。Chaum[2]首次提出盲签名概念，盲签名是一种特殊的数字签名，是指签名者在不知道消息的具体内容的情况下进行签名，并且当该签名公布后，签名者不能将自己的签名与消息对应，这一性质称为盲性。由于盲签名具有盲性，可以有效保护所签署消息的具体内容，所以在电子商务和电子选举有着广泛的应用。然而，签名人不知道所签消息的任何信息，这样的完全盲性很容易造成签名的非法使用。为了解决盲签名匿名性和可控性之间的矛盾，即在保证盲签名的不可伪造性、不可抵赖性和盲性的同时解决签名滥用，1996 年，Abe等[3]首次提出部分盲签名的概念。部分盲签名结合了盲签名的特点，在部分盲签名方案中，签名人在盲签名时可以加入与用户协商的消息或者自己的信息，消息提供者不能篡改签名人加入的信息，从而阻止签名申请者提供非法信息而滥用签名，这样既有效地保护了用户的隐私又让签名者对所签署的内容部分可控。这比盲签名更加实用，所以部分盲签名立刻成为密码学领域的研究热点。

Chow等[4]首次提出了一个基于身份的部分盲签名方案，并详细的证明了方案的安全性。随后，人们相继提出了基于身份的部分盲签名方案[5-7]。张小萍等[8]提出基于身份的盲签名方案，但是该文章没有给出方案的安全性证明。李明祥等[9]提出一种高效的基于身份的部分盲签名方案，文献中详细的给出了方案的安全性证明，但方案的效率不高。余丹等[10]提出了无证书部分盲签名方案，该方案效率上有很大优势，但并没有详细的安全性证明，所以无法确定该方案的安全性。同样的李明祥等[11]提出一个高效的无证书部分盲签名方案，但没有给出方案的安全性证明。荣维坚[12]提出无证书部分盲签名方案，给了出方案的安全性证明，但没有进行效率比较。何俊杰等[13]提出基于身份部分盲签名方案的分析与改进，但已被证明是不安全的。邓伦治等[14]提出了基于身份的高效代理方案并且在基于n-CDH问题下证明了方案的安全性。尹恒等[15]在基于CT-ACDH困难的假设下，设计了高效安全的基于身份的部分盲签名方案并且完整的证明了方案的安全性，方案的效率相较于其他方案也有明显的提高。毛昱昉等[16]基于n-CDH问题提出了基于身份的盲签名方案并证明了方案的安全性。曹素珍等[17]提出一个改进的基于身份的部分盲签名方案，在基于离散对数困难问题下证明了方案的安全性。

本文先对刘二根等[18]的方案进行分析，然后构造一种新的方案。本文在随机预言模型下，基于双线性映射的逆问题证明了方案的安全性，并且证明了方案的部分盲性和可抵抗篡改公共信息攻击。

1 准备

1.1 双线性映射

设G1、G2分别是阶为q的循环加法群和乘法循环群。e:G1×G1→G2是一个满足下列要求的双线性对映射：

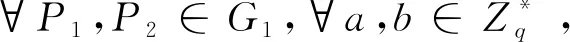
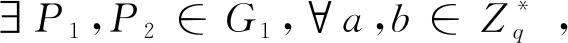
对∀P1,P2∈G1，存在一高效的计算方法可以计算出e(P1,P2)。

1.2 双线性映射的逆问题的定义

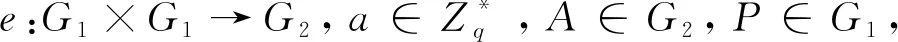
2 对刘二根方案的安全性分析

2.1 方案回顾

1)系统初始化

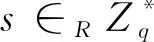
2)密钥生成

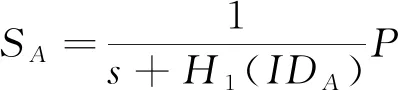
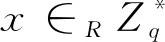
3)签名：设签名者A的身份为IDA，请求者B的身份为IDB，待签名消息为m∈{0,1}*，设A和B事先协商好的公共信息为c，计算gc=e(H3(c),P1)并作为公钥参数公开，签名者A和请求者B进行如下交互：

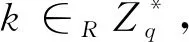
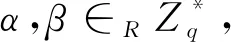
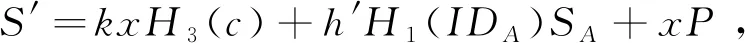
(4)解盲：B收到盲签名后S′进行解盲，计算S=αS′，则消息m的部分盲签名为δ=(S,m,h,r,c)

4)验证：验证者M收到消息m的签名δ=(S,m,h,r,c)后，验证等式

r=e(S,Ppub+H1(IDA)P)g-hH1(IDA)是否成立。如果成立，则接受签名，否则，签名无效。

2.2 对方案的攻击

如果攻击者篡改公共信息，那么就会存在签名被滥用的可能。具体攻击过程如下：

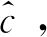
方案变的部分只有签名者A和请求者B进行的交互和验证部分，方案的其余部分都不变。签名者A和不诚实的用户T进行如下交互：

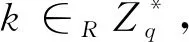
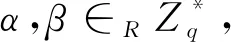
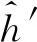
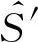
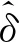
下面证明，如果被不诚实的用户T篡改过公共信息的签名能通过验证等式，则说明攻击者攻击成功，也即方案不能抵抗篡改公共信息攻击。

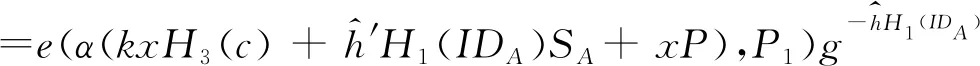
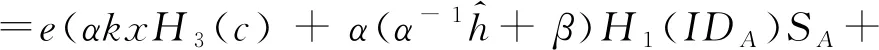
=r

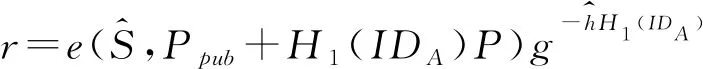
3 本文提出的基于身份的部分盲签名方案

1)系统初始化

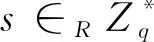
2)密钥生成

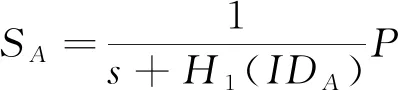
3)签名

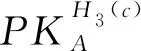
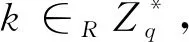
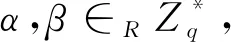
(3)签名：A收到盲化消息U后，进行签名，计算V′=kSA+H3(c)xAU，并且将V′发送给B；

(4)解盲：B收到盲签名后V′进行解盲，计算V=αV′，则消息m的部分盲签名为δ=(V,m,h,R,c)

4)验证

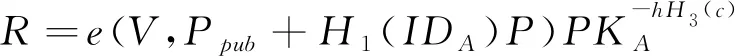
4 方案的安全性分析

4.1 正确性

定理1 所提基于身份的部分盲签名方案是正确的。

证明只要部分盲签名δ=(V,m,R,c)能够通过验证等式即可。具体验证过程如下：

e(V,Ppub+H1(IDA)P)PKA-hH3 (c)

=e(αV′,Ppub+H1(IDA)P)PKA-hH3 (c)

=e(α(kSA+H3(c)xAU),PA)PKA-hH3 (c)

=e(αkSA+αH3(c)xAU,PA)PKA-hH3 (c)

=e(P,P)αkPKAαH3 (c)PKAhH3 (c)e(xAP,PA)αβPKA-hH3 (c)

=KαPKαβ

=R

4.2 方案可抵抗篡改公共信息攻击

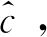
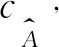
方案变的部分只有签名者A和请求者B进行的交互和验证部分，方案的其余部分不变。

签名者A和不诚实的用户T进行如下交互：

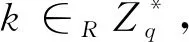
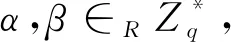
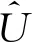
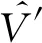
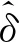
下面证明篡改了公共信息之后就不能通过验证等式：

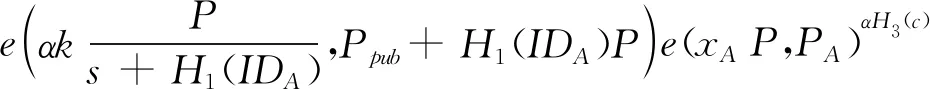
≠KαPKαβ

≠R

4.3 不可伪造性

定理3 在随机预言模型和基于双线性映射的逆问题困难的假设下，提出的方案对自适应选择消息及身份攻击是存在性不可伪造的。

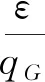
为了能够计算出T∈G1，挑战者C与攻击者F进行交互，挑战者C通过回答攻击者F的H1，H2，H3哈希询问、个人公钥询问、部分密钥询问、个人密钥询问和签名询问分别设置相应的列表：L1(IDi，h1i)，L2(mi，Ri，h2i)，L3(ci，h3i)，LG(IDi，PKi)，LJ(IDi，Si)，Lj(IDi，xi)，Lδ(Vi，mi，hi，Ri，ci)。这些列表初始为空，列表值由随机预言机模拟回答。F至多做qH1次H1询问，qH2次H2询问，qH3次H3询问，qG次个人公钥询问，qJ次部分密钥询问，qj次个人密钥询问，qδ次签名询问。具体的交互过程如下：

系统设置设目标用户的身份用ID*表示，挑战者C首先生成并公布系统公开参数params，其中系统公钥设置为Ppub=sP，即设置系统主私钥为s。

H1询问C设置L1(IDi，h1i)，C接收到F关于身份为IDi的H1询问。C首先查询列表L1，若表中存在(IDi，h1i)项，则直接返回h1i给F；否则：

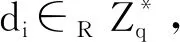
2)若IDi=ID*，则C令h1*=t-s，将h1*返回给F，并将(IDi，h1*)添加到列表L1中。

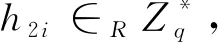
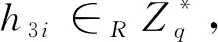
个人公钥询问C设置LG(IDi，PKi)，C接收到F关于用户身份为IDi的个人公钥询问。C首先查询列表LG，若表中存在(IDi，PKi)，则将PKi返回给F；否则，假设之前已经进行过了H1询问，不然就先进行H1询问：

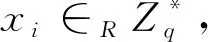
2)若IDi=ID*，则C计算P*=sP+h1*P=sP+(t-s)P=tP，设置PK*=W，将PK*返回给F，并将(IDi，PK*)添加到列表LG中。

部分密钥询问C设置LJ(IDi，Si)，C接收到F关于用户身份为IDi的部分密钥询问。C首先查询列表LJ，若表中存在(IDi，Si)，则将Si返回给F；否则，假设之前已经进行过了H1询问，不然就先进行H1询问：

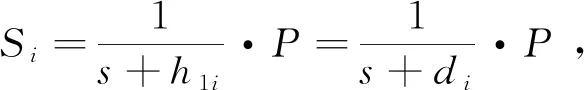
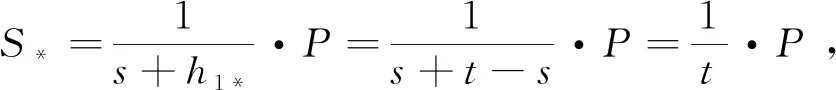
个人密钥询问C设置Lj(IDi，xi)，C接收到F关于用户身份为IDi的用户个人密钥询问。C首先查询列表Lj，若表中存在(IDi，xi)项，则将xi直接返回给F；否则：

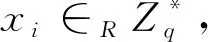
2)若IDi=ID*，C拒绝回答个人私钥，询问终止。

签名询问C设置Lδ(Vi，mi，hi，Ri，ci)，C接收到F关于消息为mi的签名询问。C首先查询列表Lδ，若表中存在(Vi，mi，hi，Ri，ci)项，则直接返回给F；否则，假设之前已经进行过哈希询问，不然就先进行上述的哈希询问：

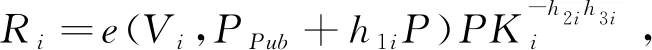
2)若IDi=ID*，则按以下步骤进行：

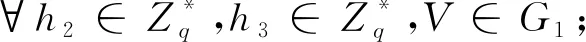
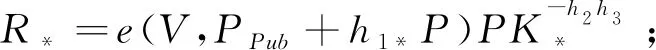
③令h2=H2(m,c,R)，h3=H3(c)，储存(m,c,h2,h3,R)，若产生碰撞，则重做①至③。

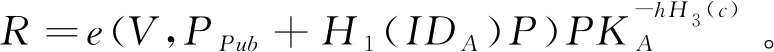
所以有：

e(V*，sP+(t-s)P)W-h*H3(c*)=

e(V*，tP)e(T,tP)-h*H3(c*)=

e(V*，tP)e(-h*H3(c*)T,tP)=

e(V*-h*H3(c*)T,tP)=

即：

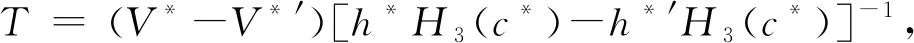
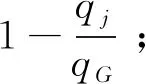
所以，在双线性映射的逆问题困难下，方案在适应性选择消息和身份攻击下对超级攻击者F是存在性不可伪造的。

4.4 方案盲性

定理4 所提部分盲签名方案满足部分盲性。

证明给定一个有效的部分盲签名δ=(V,m,h,R,c)和任意一组签名者保存签名过程中的交互中间变量(k,K,V′,h′)，可知：

V=αV′

(1)

(2)

(3)

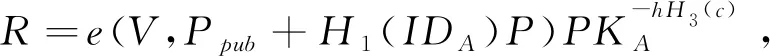
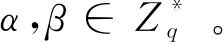
4.5 效率对比分析

本文所提方案与以前方案的效率比较如表2所示，表1中所涉及到的对比数据来自文献[19-20]。通过表2 的计算效率对比可看出，本文方案的运算效率相较于其他方案有提高。

表1 运算效率Tab.1 operational efficiency

表2 本文方案与其他4种方案计算效率比较Tab.2 Comparison of computational efficiency between the scheme and the other four schemes

5 结语

部分盲签名方案允许签名者在不损害盲性的前提下将与用户提前商议好的公共信息包含在签名中，消息和最终签名对签名者都是未知的，这有效的防止了签名被滥用。这一特性使得部分盲签名在匿名电子投票、电子现金系统、电子商务、电子选举等方面有着广泛的运用。本文的方案克服了公共信息被篡改的缺陷，并在基于双线性映射的逆问题的困难假设上证明了方案的安全性。与文献[9-10,15]进行效率比较，本文的方案只需要1次双线性对计算，5次标量乘运算，5次幂乘运算，2次求逆运算，效率上有提高。