围护桩最小变形的支撑位置求解方法及应用★

卓赛扬 何甘霖 王立峰

(东北林业大学土木工程学院，黑龙江哈尔滨 150040)

1 概述

在桥梁、高层建筑以及地铁车站等工程的基础施工中，基坑支护技术的应用非常广泛。较为典型的基坑支护结构是通过先施工周边围护桩和围囹(圈梁)，再构筑内支撑的形式来完成［1-3］。在实际工程中，围护结构和内支撑的形式多样，需要根据基础或地下构筑物的结构形式、平面尺寸和深度、工程地质水文等多种因素来决定。但是减少基坑围护结构的变形，一般是各类基坑支护设计中的重要目标，以减少基坑周围地表沉降和对周边环境的影响［4-6］。

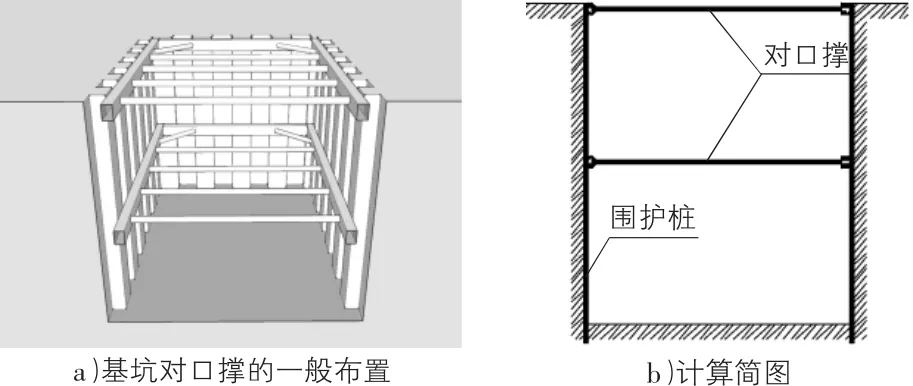
图1 狭长矩形基坑的支撑示意图

在以往的基坑支护设计中，一般的做法是先根据工程经验完成基坑的内支撑布置，再对其进行结构分析验算。在保证围护结构受力安全性的同时，有时会调整内支撑的布置，尽量减少围护结构的侧向位移［7-9］。

对于狭长矩形基坑，为加强围护结构的强度与刚度，采用对口支撑的方式最为直接有效，如图1所示。

本文以减少围护桩的侧向变形为目标，建立简化的结构计算图示，研究对口撑位置的确定方法。

2 双层对口撑围护桩结构分析模型及求解

2.1 简化计算模型

以某长条状基坑为例，采用密集围护桩帷幕，设置上、下两层对口撑，为保持基坑顶部的稳定性，上层对口撑一般位于围护桩的顶部。这里，以围护桩侧向变形的最小化为目标，求解下层对口撑的位置。建立围护桩支撑结构的计算模型，见图2，按照对口撑的有效支撑范围，选取围护桩结构的刚度，桩侧土压力可以按三角形分布简化。以两道对口撑的支撑反力为冗余力，分别画出悬臂围护结构在侧向土压力和两个冗余力作用下的变形示意图，如图3所示。

图2 两层围护桩计算模型

2.2 用对口撑轴力表达的围护桩结构弯矩

当侧向土压为三角形分布时，根据图2所示的坐标系，围护桩结构的弯矩为:

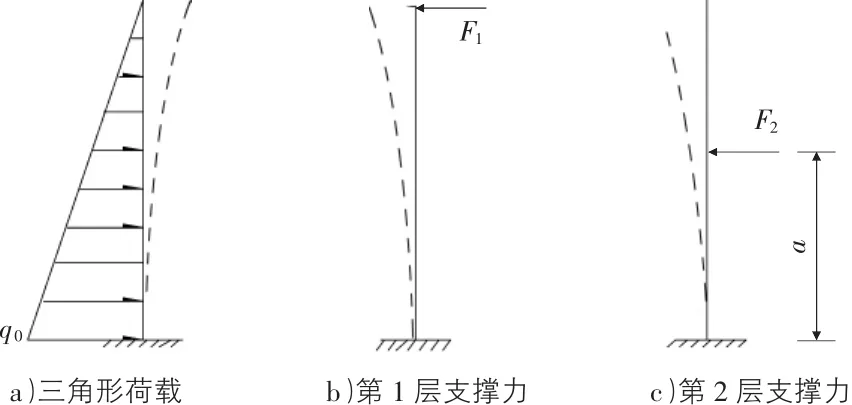
图3 侧向土压及支撑力作用下的变形

当第1层对口撑的轴力为F1时，此时围护桩结构的弯矩为:

当第2层对口撑的轴力为F2时，此时围护桩结构的弯矩为:

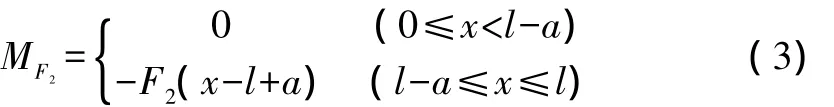
由式(1)～式(3)，根据叠加原理，围护桩结构的总弯矩M=Mq+MF+MF，可得:

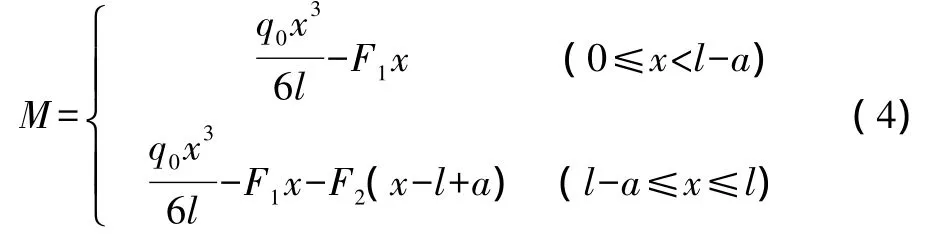
2.3 对口撑轴力的求解

围护桩结构的弯曲应变能，可表示为:

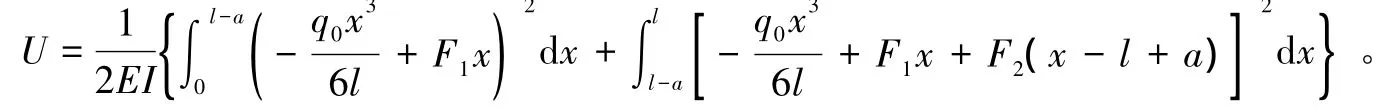
简化计算后可得:

假设对口撑刚度无限大，围护桩在支撑点处的变形为 0，由卡氏第二定理可得:

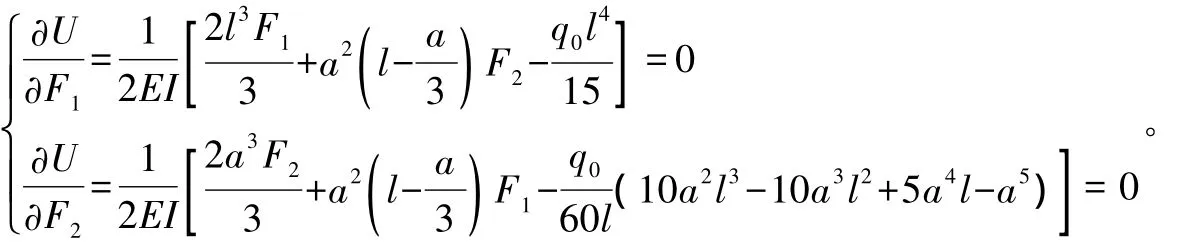
通过联立求解上式两个方程，解得两道对口撑的轴力为:

2.4 围护桩结构变形的求解

由结构力学分析可以得到，在三角形线荷载作用下围护桩结构的侧向变形曲线为:

在集中力F1作用下的结构挠曲线方程为:

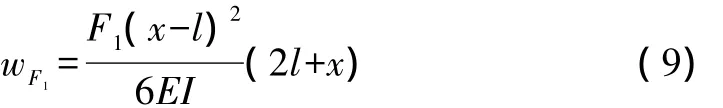
在集中荷载F2作用下的结构挠曲线方程为:

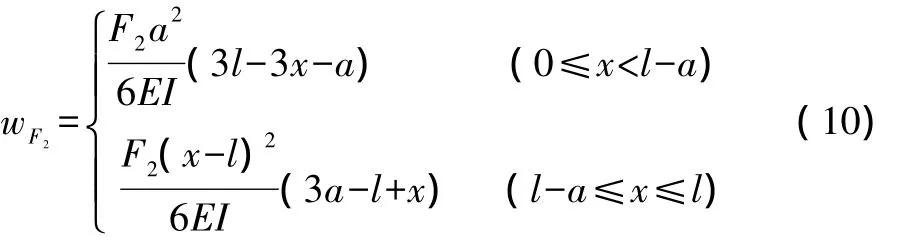
根据线弹性范围的叠加原理，可将上述公式分段叠加:

代入式(8)～式(10)，可得围护桩结构的挠度曲线方程:

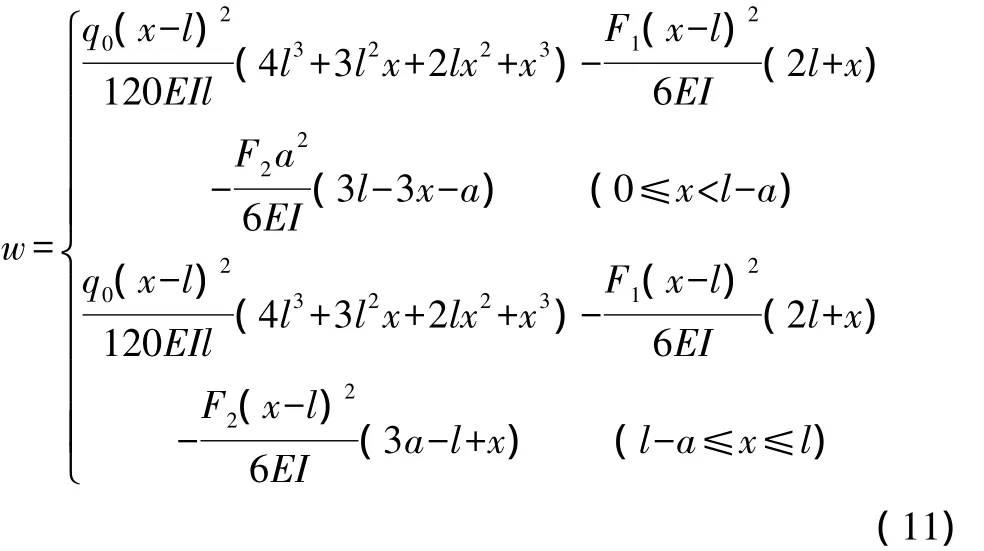
荷载组合下的围护桩变形示意图见图4。

图4 荷载组合下变形示意图

2.5 基于围护桩最小侧向位移的对口撑位置确定方法

在上述得到围护桩结构变形表达式的基础上，设第1层～第2层对口撑之间的挠曲变形量为w1，第 2层对口撑～设计坑底之间的挠曲变形量为w2，如图4所示。设定当w1max与w2max基本相等(设容差不大于2%)，围护桩的变形最小，平面对口撑的位置最优，下面求此时的值。

由于式(11)中的w表达式包含a3，x5，属于高次方程，随着a值的不同，存在多个拐点，不易得出a的解析解。

为了求解围护桩在最小变形时的对口撑位置，本文提出迭代算法。计算流程为:首先平均分配对口撑之间的间距(即取a=l/2)，由式(6)，式(7)和式(11)，可以计算出w1max和w2max，初步比较两个挠曲变形数值，缩小挠曲变形量较大的支撑计算间距(即给个增量Δa+a重新赋予a)，重复上一步计算，再比较两个挠曲变形数值，直到对口撑层间的最大变形值基本相等(设容差不大于2%)，确定最终的目标a值，此时对口撑的位置最优。

3 三层对口撑围护桩结构分析模型及求解

1)对三层对口撑，建立围护桩支撑结构计算模型，见图5。

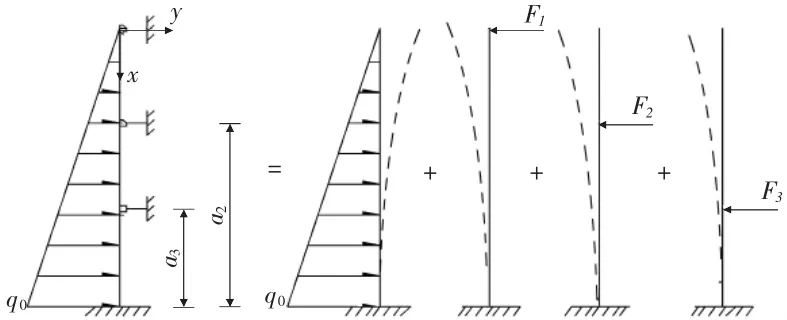
图5 三层围护桩计算模型及侧向土压及支撑力作用下的变形分解

2)围护桩结构的弯曲应变能，可表示为:

假设对口撑刚度无限大，围护桩在支撑点处的变形为 0，由卡氏第二定理可得:

通过联立求解上式三个方程，解得三道对口撑的轴力 为:

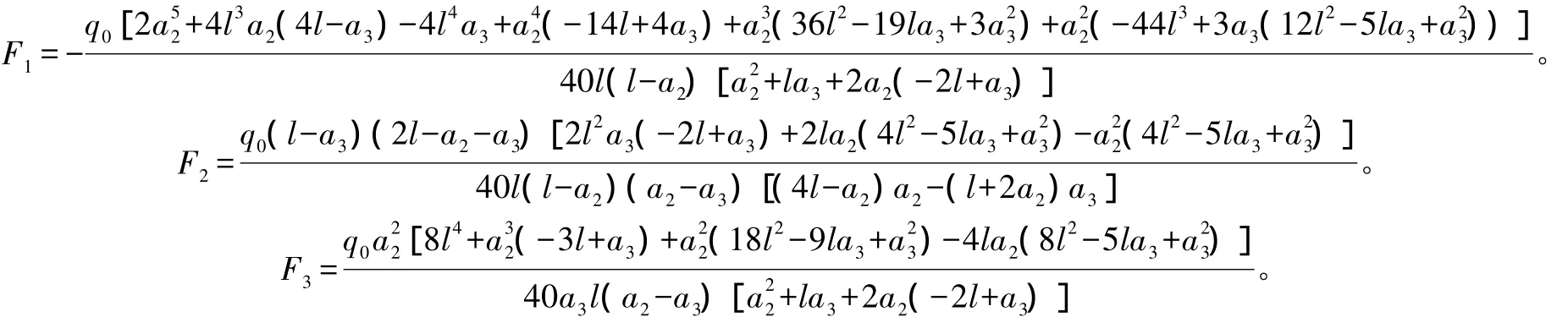
3)同理，可得围护桩结构的挠度曲线方程:

上述推导的对口撑轴力和挠度曲线方程，如果将q0，l，EI等不变数值代入的话，公式的形式将会大大简化。

4 求解多道对口撑位置的一般步骤

前面针对2道及3道对口撑的情况，给出了基坑围护桩结构最小变形的求解方法。实际上，深基坑往往可能需要设置多道对口撑，参照上述思路，针对多道对口撑和一般侧向土压q(x)分布，以围护桩变形最小化为目标，下面给出求解多道对口撑位置的一般步骤。

多道对口撑围护桩结构的计算模型见图6。

图6 一般土压力作用下多道对口撑围护桩结构计算模型

1)假设对口撑的初始位置ai，例如均分基坑高度。

2)建立如图6b)所示的坐标系，采用上一节的方法，同样可以给出围护桩的弯矩表达式:

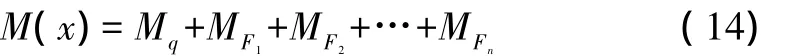
式(14)中包含 F1，F2，…，Fn，ai的一次项，以及 x 的三次项。

3)求解各道支撑处的集中力Fi。

围护桩的弯曲应变能表达式:

式(15)中包含 F1，F2，…，Fn的二次项，以及 ai的高次项。

假设对口撑刚度无限大，根据卡氏第二定理可得:

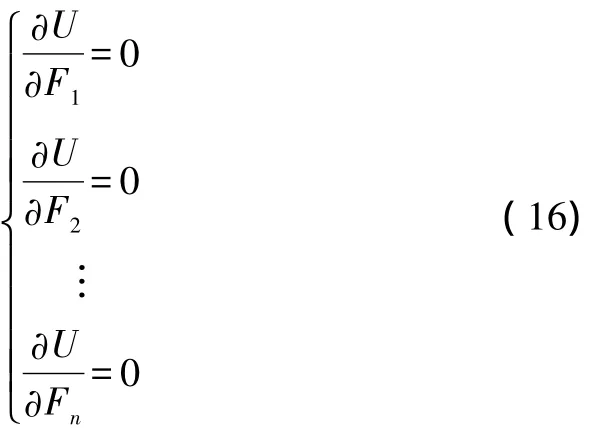
可以得到n个一元一次方程组，其中Fi为一次，可以解出各道对口撑的轴力 F1，F2，…，Fn，Fi中含参数 ai。

4)求解围护结构的变形。

参照双侧及三层支撑，同理，根据结构力学分析，由q(x)，F1，F2，…，Fn，可以给出各荷载作用下围护桩结构的侧向变形曲线 wq，wF1，wF2，…，wFn，根据叠加原理，可将上述公式分段叠加得到:

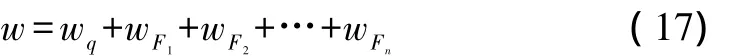
式(17)中，含有ai的高次项、x的高次项和 Fi的一次项。

5)迭代算法求解各道支撑至地面的距离ai。

基于围护桩最小侧向位移的支撑位置迭代计算，设第i层～第i+1层对口撑之间的围护桩挠曲变形量为wi，经数值计算当wimax基本相等(容差不大于2%)时，围护桩的变形最小，此时各道对口撑的位置最优，下面给出此时ai值的计算方法。

首先平均分配各道对口撑之间的间距(即取ai=l/n)，由式(16)得到的Fi表达式和式(17)，可以计算出各层支撑之间的wimax，初步比较围护桩各段的挠曲变形数值，适当缩小挠曲变形量较大的支撑计算间距，适当增加挠曲变形量较小的支撑计算间距，即调整对口撑层间的间距，将增量Δai+ai重新赋予ai，重复上一步计算，再比较围护桩各段的挠曲变形数值，不断迭代计算，直到对口撑层间的最大变形值基本相等(设容差不大于2%)，确定最终的ai值，此时对口撑的位置最优。基于围护桩最小侧向位移的支撑位置迭代计算流程见图7。

图7 以围护桩侧移最小化为目标的支撑位置求解流程

5 算例分析及变形测试

以五峰山过江通道南北公路接线工程的某特大桥水中墩32号围堰为例，钢板桩围堰平面尺寸为39.6 m×10.8 m，采用拉森Ⅳw型钢板桩，竖直平面内共设置两层内支撑，采用2HM588×300型钢，拉森钢板桩的布置形式及内支撑标高见图8，封底混凝土底面标高为5.44 m。

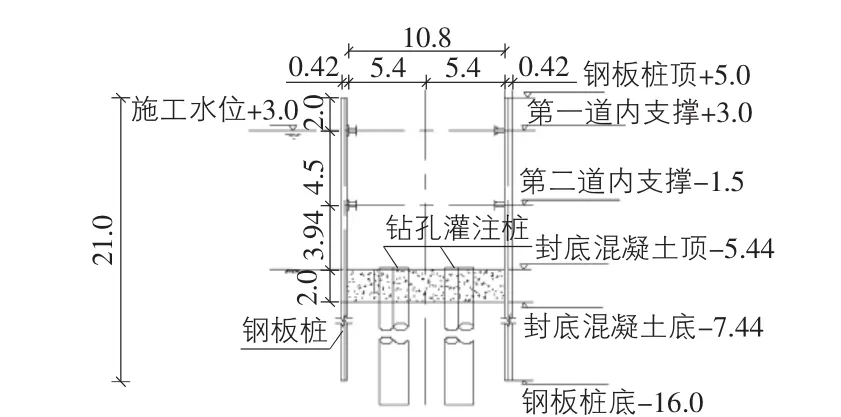
图8 钢板桩围堰侧立面布置图（单位:m）

将围护桩简化成图 2所示模型，设 l=8.44 m，q0=84 400 N/m，每米宽的钢板桩刚度EI=11 340 000 N·m2。根据图7的算法，可以给出支撑等分及优化设计(即不同a值)时，围护桩的变形曲线见图9，可以看出支撑等分时围护桩的位移达到5.7 mm;优化设计取a=3.87 m，侧向位移达到最小，为3.7 mm。芒稻河特大桥32号墩基础，采用两道支撑优化后的方案进行施工，采用金码JMZX-74XXY测斜探头及JMZX-7000综合测试仪表对钢板桩桩身的变形进行跟踪监测。扣除支撑的压缩变形影响，钢板桩的实测变形值为3.8 mm，误差值小于3%，满足使用要求。

如采用三层对口撑，其他条件同上，根据图7的算法及应用程序，可以给出支撑位置等分及优化设计(即不同a2和a3值)时，围护桩的变形曲线见图10，可以看出支撑位置等分时围护桩的位移达到1.1 mm;优化设计取a2=5.21 m 和 a3=2.46 m，围护桩侧向位移达到最小，为0.62 mm。

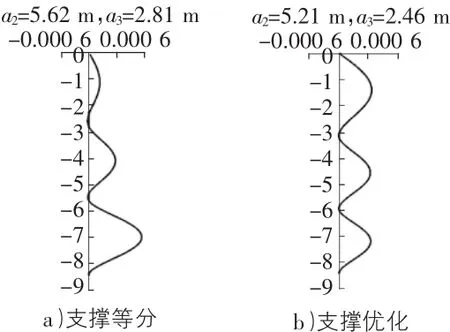
图10 三层支撑不同ai值下的围护桩变形挠曲线（单位:m）

6 结语

在各类基坑支护工程中，减小围护桩结构的侧向变形，常常是围护结构内支撑设计的主要关键。本文以围护桩侧向变形的最小化为目标，给出优化对口撑位置的一般方法，主要研究结论如下:

1)给出了围护桩结构的简化计算模型，并且以两层及三层对口撑情况为例，应用卡氏第二定理，给出了对口撑的支反力解析表达式;

2)进一步通过分段叠加的方法，给出了围护桩的连续挠曲线方程;

3)提出以减小围护桩侧向位移为目标的迭代算法和求解流程，通过数值分析，可确定对口撑最佳的布置位置;

4)以某特大桥水中墩的32号基础围堰设计及施工为例，给出了设计算例和实际测试结果对比，误差满足工程要求。