偏心受压构件承载力计算问题探讨
飞俊杰 蒋 源
(云南水利水电职业学院,云南昆明 650499)
在实际工程中,偏心受压构件应用非常广泛,工业厂房排架柱和框架顶层边柱往往属于大偏心受压,高层建筑的下部几层往往属于小偏心受压。其中矩形截面偏心受压构件最为基础和常见,正确地对其受力分析、承载力计算、合理地选择配筋形式,是设计者经常要面对的一个问题,恰当的分析和计算将会给建设减少不必要的工程投资。
1 偏心受压构件计算理论
1.1 计算假设
为简化计算,正截面承载力计算基于《混凝土结构设计规范》[1](以下简称《规范》)的基本假设:
1)平截面假设。正截面变形后仍保持平面。
2)不考虑受拉区混凝土的抗拉强度。
3)混凝土受压区的应力与应变关系理想化,当采用强度等级C50及以下混凝土时,混凝土压应变εcu=0.003 3,纵向钢筋的极限拉应变εy=0.01。
4)纵向钢筋的应力取钢筋应变与其弹性模量的乘积σs=εsEs,但其绝对值不大于其相应的强度设计值σs≤fy。
1.2 大小偏压基本判别
偏心受压构件的受力可按大偏心受压与小偏心受压两种受力状态进行分析。大小偏心受压的基本判别方法是通与界限相对受压区高度ξb比较判别,当ξ≤ξb时,截面属于大偏心受压状态;反之当ξ>ξb时,则属于小偏心受压。
1.3 基本计算公式及限制条件
基于计算假设,根据大偏心受压计算受力图1,用力平衡方程写出其计算公式:

其中,e=ei+0.5h-as。
公式适用条件:
1)保证破坏时受拉钢筋先屈服:ξ≤ξb。
2)保证破坏时受压钢筋应力能达到屈服:x≥2a's。
若x≥2a's,取x=2a's,这时混凝土抗压力与受压钢筋A's抗压力共线,对受压钢筋合理点取矩有:

同理,根据小偏心受压计算受力图2,用力学平衡方程写出小偏心受压计算公式。
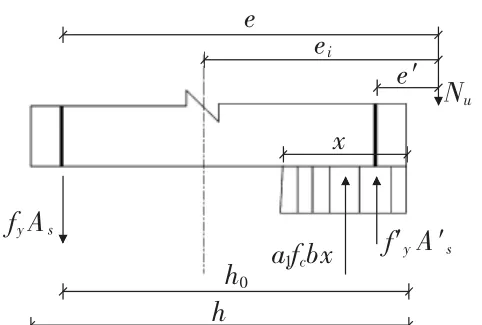
图1 受力图(一)
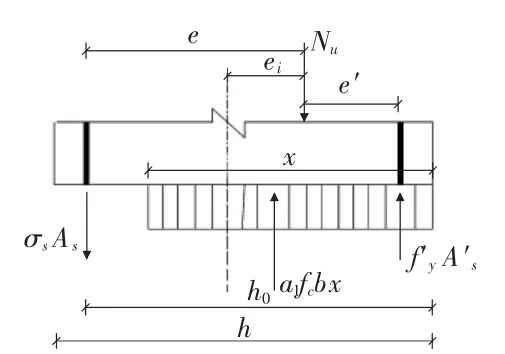
图2 受力图(二)
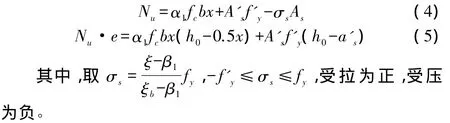
2 不对称配筋计算
在进行不对称配筋偏心受压构件正截面设计时,无法求出ξ的大小,因此上述基本判别方法无法使用。根据工程经验,通常按初始偏心距 ei的大小进行判别,当 ei>0.3h0时,可初步按大偏心受压进行计算;当 ei≤0.3h0时,可初步按小偏心受压进行计算。但最终还需要根据基本判别方法校核。
2.1 大偏心受压截面设计问题
若ei>0.3h0,一般可按大偏心受压计算。分别有以下两种情况:
情况1:A's,As均未知。两个基本公式对应三个未知数A's,As,x,故无唯一解,为保证钢筋用量最省,即 min(A's+As),充分发挥混凝土抗压能力,故取x=ξbh0。
计算时,用式(2)求出A's;然后用式(1)求出As。
情况2:A's已知。两个基本公式对应两个未知数As,x,有唯一解。
计算时,先用式(2)求出受压区高度x。
1)当 2a's≤x≤ξbh0,用式(1)计算 As;
2)当 x<2a's,取 x=2a's,用式(3)计算 As;
3)当x>ξbh0,应改用小偏心受压重新计算;如果不改变截面尺寸或不提高混凝土强度等级,仍按大偏心类型计算,说明受压区钢筋A's配量不足,按A's,As,x未知类型重新计算。
2.2 小偏心受压截面设计问题
若ei≤0.3h0时,按照小偏心受压情况计算,两个基本方程对应三个未知量A's,As,x,故无唯一解。在一般情况下,小偏心受压破坏时,远离轴压侧钢筋As无论受拉、受压都无法屈服,当轴压力N≤α1fcbh时,按照《规范》规定的最小配筋率取值As=0.2%bh;当轴压力N>α1fcbh时,应该 验 算 反 向 破 坏 的 承 载 力[2],取 As=max
按小偏心受压计算式(4),式(5),可求出ξ,根据相对受压区高度ξ不同值,对应有以下三种情况:
1)若 ξb<ξ≤2β1-ξb时,破坏时远离轴压力一侧钢筋 As不论拉、压均未屈服。这时将ξ代入小偏压计算公式计算出A's;

2.3 偏心受压构件截面复核问题
2.3.1 弯矩作用平面的承载力复核
弯矩作用平面的承载力复核有两种情况:
1)给定轴力N,求弯矩作用平面的弯矩设计值M;
取 x=xb= ξbh0代入式(1),有 Nb= α1fcbξbh0+f'yA'sfyAs。若N≤Nb,为大偏心受压,由式(1)求出受压区高度x,再用式(2)求出 e,根据 e=ei+0.5-as求出 ei,再由 ei=e0+ea确定 e0,从而有 M=Ne0;若 N>Nb,为小偏心受压,由式(4)求出受压区高度x,再用式(5)求出e,之后步骤同上述大偏心受压一致。
2)给定轴力作用的偏心距e0,求轴力设计值N;
对竖向作用点取矩求受压区高度x。若x≤xb,为大偏心受压,再由式(1)求出N;若x>xb为小偏心受压,联立式(4),式(5)求出 N。
2.3.2 垂直于弯矩作用平面的承载力复核
无论是截面设计或截面复核问题,是大偏心受压还是小偏心受压,都应根据长细比,确定稳定系数φ,按轴心受压的情况式(6),验算垂直于弯矩作用平面的受压承载力。
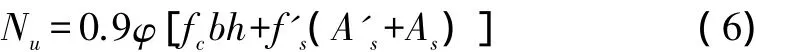
3 对称配筋计算
在实际工程中,偏心受压构件在不同内力组合下,可能有反向的弯矩,采用对称配筋使设计偏于安全。同时对称配筋还可以避免施工差错,装配式柱为保证吊装不出错,一般采用对称配筋。对称配筋即:A's=As,fy=f'y,as=a's。
3.1 对称配筋截面设计
对称配筋时,把A's=As代入式(1),有:

当ξ≤ξb时,按大偏心受压构件设计。计算时又有以下两种情况:

2)若 x<2a's,取 x=2a's,用式(3)计算 As。
当ξ>ξb时,按小偏心受压构件设计。联立式(4),式(5),有:

这时需解关于ξ的一元三次方程,为使计算简化,根据《规范》取 ξ(1-0.5ξ)=0.43,把式(8)简化为关于 ξ的一元,进而求出A's。
3.2 对称配筋截面复核
其截面复核计算同不对称配筋情况一致,不再累述。
4 计算探讨
在解决偏心受压构件承载力计算时,除了满足计算公式要求外,还需保证计算结果符合构造要求,同时还要理解计算时出现的各类特殊情况的意义及解决方法,设计时在安全可靠和工程造价间找到平衡点。
4.1 大偏压计算时受压区钢筋负值情况
在实际设计中截面尺寸较大的构件在大偏心受压计算时,经常会出现A's<0的情况[3],这是因为受压区的混凝土的抗压强度有富余,不需受压钢筋。针对这种情况,可按最小配筋取A's=0.2%bh,进而计算As时,但所求x大概率出现x>xb的情况,应按小偏心受压处理;如若要按大偏心受压计算,可以采用对称配筋的方式取A's=As进行求解。
4.2 配筋方式
通过文献[4]计算对比,可知对称配筋的钢筋总面积都比非对称配筋总面积要大,但对称配筋形式计算简单、便于操作、偏于安全。非对称配筋能够充分利用材料强度,经济效益高。所以在实际工作中,需根据不同的情况和需求采用相适应的方法,在保证构件安全可靠的同时需考虑节约钢筋用量,降低工程成本。
4.3 计算流程
偏压构件截面计算问题内容多、概念多、公式多,且情况复杂。但经过分析整理,可把问题归结为“作受力图→列力的平衡方程→按最优设计补充方程(若需要)→求解方程(进行相应简化,避免求解3次方程)→满足构造要求”[5]。
5 结语
通过矩形截面偏心受承载力计算问题的论述,对计算中可能出现的特殊情况进行解释说明,对处理各类计算的方法进行详细介绍,对不同配筋方式进行比较,同时总结归纳整个计算问题的核心思想和流程,能够帮助结构设计人员更好地理解和应用相关知识。

