参数法和非参数法VaR模型在股市风险中的比较研究——基于沪深300指数的实证研究

岳昊敏， 孙英隽

(上海理工大学 管理学院， 上海 200093)

0 引 言

VaR(Value-at-Risk)即“风险价值”模型，于1993年作为度量市场风险的工具而被提出。目前，国内外大部分金融机构均广泛使用VaR的方法衡量金融风险。作为一种对于金融市场各类资产风险的度量，它表示在一定概率下，一个金融资产在将来一刻或一段时间区间极大的可能损失值。其数学定义为：在给定置信度p的条件下，如果用对数收益率R衡量损失，VaR即满足该式的值：Pr(-RPF>VaR)=p，Pr(RPF<-VaR)=p。也就是说，金融资产的收益率不小于-VaR的概率为1-p，小于-VaR的概率为p。如果能准确估计出金融资产未来一段时间内的VaR，对于企业做出投资决策有重要意义。

1 文献综述

VaR模型自产生以来已经得到了广泛的发展。朱立芬认为，VaR模型不仅对风险控制，甚至是绩效评估及信息披露均是优质的选择[1]。Paye[2]提及历史模拟法作为非参数方法，能够去测度风险。黄剑[3]对HS、WHS及拔靴法在商业银行利率风险的运行效果进行测度。刘辉等表明，若波动性变化时传统历史模拟法对市场风险的计算会被高估或低估[4]。通过股价、汇率证明，加权历史模拟法是历史模拟法的改进[3]。随着科技的发展，参数度量方法孕育而生，GARCH模型的运用也逐步发展。实证表明，半参数与GARCH模型的方法更有效，对我国证券市场的市场风险能够较好地刻画[5]。孙亮等运用EGARCH、TARCH等模型，对上市公司短期海外并购风险进行度量，度量结果证明VaR模型作为风险度量方法的结果可靠性高[6]。张琼实证表明EGARCH、PGARCH模型能够准确地对中国股市上证指数和道琼斯股票市场指数进行风险度量[7]。Madhusudan Karmakar利用极端价值理论(EVT)估计印度股市的动态风险价值表明，估计分位数风险度量具有准确性和可靠性[8]。谢合亮等提及蒙特卡洛模拟法，采用抽样产生同均值同方差的随机序列，克服了在计算非线性资产组合时的缺陷，逐渐成为一种重要的工具去计算VaR[9]。

本文根据相关文献，选取非参数法中的历史模拟法，并增加指数加权历史模拟法，对于参数法的选择，由于非线性GARCH模型可以刻画过去正负扰动的非对称波动率响应。创新性的选择NGARCH模型，以正态分布、学生t分布为假设，研究在不同置信水平下，寻找最优预测模型。采用NGARCH模型结合EVT模型以及蒙特卡洛模拟法，对于未来一日的VaR进行预测，对 VaR的研究进一步扩展，为金融风险的度量提供现实依据。

2 测度方法与模型

2.1 非参数法

2.1.1 历史模拟法(Historical Simulation)

历史模拟法通过每次取一定长度的历史数据作为样本，将样本的分布看作是整体分布。在置信度p下，只需要找到这些历史数据的p分位数，以这些历史数据的p分位数就可以表示VaR。即：

2.1.2 加权历史模拟法(Weighted Historical Simulation)

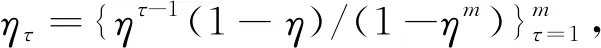
2.2 参数法

2.2.1 NGARCH模型

股票市场的收益率会受到自身残差的影响，从而表现出非对称性。由于收益率条件方差波动的非对称性难以被GARCH模型刻画，因此为了刻画这种非对称波动率响应，本文选用GARCH组模型——非对称GARCH模型(non-linear GARCH)。

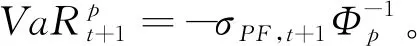
基于t分布假设的NGARCH模型中，假设如下：

RPF,t+1=σPF,t+1zt+1,withzt+1～i.i.d.t(d), where

在给定参数精确度下，估计出d及其它模型参数，随之就可以计算VaR，公式如下：

2.3 其它模型

2.3.1 EVT模型

风险的发生服从尖峰厚尾的尾部。EVT模型也可以称为极值理论，认为尾部既不服从正态分布也不服从t分布，而是服从广义帕累托分布。即：

通过设定一个阀域值u，则超出这个值即为尾部。极值部分的分布函数可以表示为：

其中，T是样本总量;Tu是极值个数。从而，VaR可以表示为：

2.3.2 GARCH-EVT模型

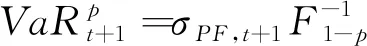
2.3.3 MONTE CARLO模拟法

蒙特卡洛模拟是一种基于某种统计分布假设的前提下，对可以描述风险因素的变化，进行随机模拟的方法。首先假设某收益率为随机过程，该随机过程根据给定的价格变动，一定量地对于将来可能发生的各种情境进行模拟，最后排序各情况下收益率。在给定收益率的分布情况下，估算不同置信水平下的VaR值。

2.3.4 MONTE CARLO-GARCH模型

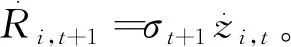
3 实证分析

本文方法与模型的运用均基于python3。数据来源于wind数据库，以日为单位，选取2011年1月4日到2019年6月4日共2 046天的沪深300指数的收盘指数作为本文的实证数据进行研究。收益率选用对数收益率，指数的对数收益率Rt+1的计算公式为：

Rt+1=lnVt+1-lnVt

其中，Vt、、Vt+1分别为第t与t+1日的收盘指数。

沪深300指数对数收益率时序如图1所示。

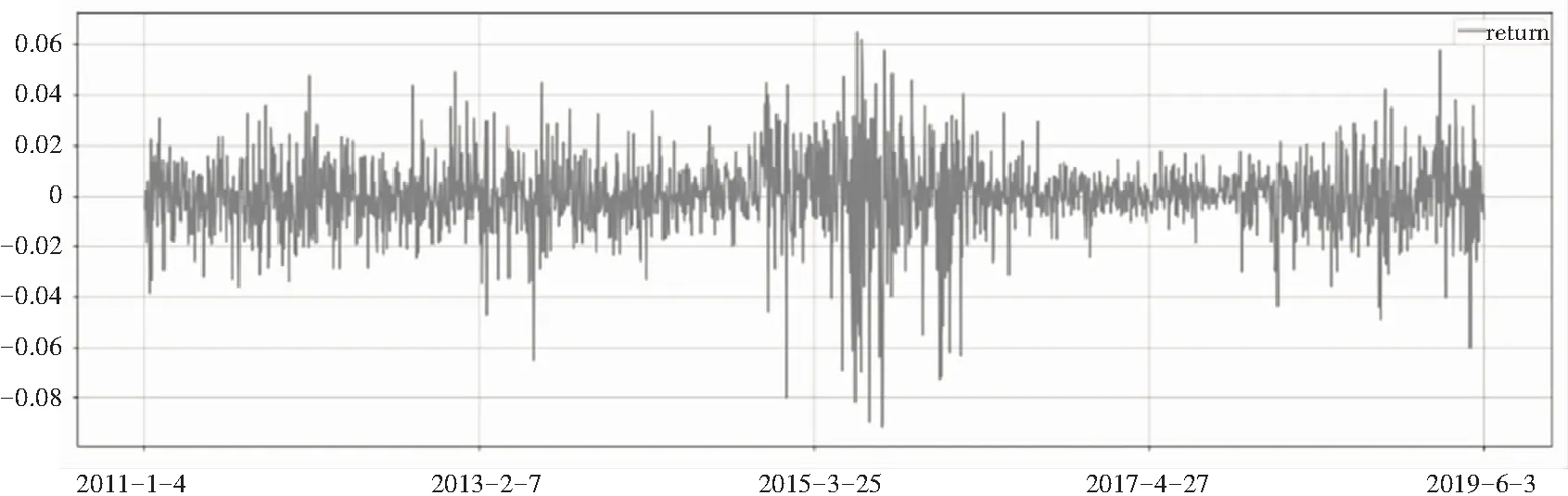
图1 收益率时序图

3.1 非参数法

运用历史模拟法(HS)以及加权历史模拟法，在1%及5%显著性下对VaR进行测度。选择移动窗口m分别为125、250、375。如移动窗口大小为250即为一年交易日综合。加权历史模拟法的η应介于0.95～0.99，本文设定η为0.99。在多种m的选择下，模拟结果见表1。

通过运行结果可以看出，对于m=250时，方法模拟效果最优。同时可以看出，移动窗口为250，在1%的置信度下，加权历史模拟法的效果最优。

表1 HS及WHS方法实测结果

3.2 参数法

运用GARCH参数法对VaR进行测度。选用GARCH(1，1)的NGARCH模型进行VaR模拟计算。在正态分布、t分布的不同假设下，参数精度为0.000 000 1的设定下，NGARCH模型进行迭代得到的参数结果见表2。

在1%、5%、10%不同置信度下的VaR测试的结果见表3。

由表3可见，在5%置信度下的正态分布NGARCH模型，模拟效果最优。经过实证，t分布下的VaR测度过于保守，尽管得到了避免投资损失的目的，但是相对而言，此时资金的持有成本过高，不利于投资机构或者投资者的操作灵活度，存在一定的局限性。

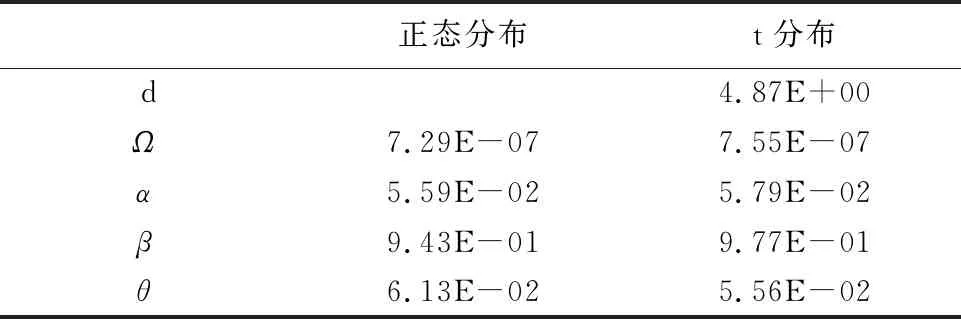
表2 不同模型下参数结果表

对于次一日的VaR测度，选择所提出的创新方法NGARCH-EVT模型、MONTE CARLO-GARCH模型进行研究。对于EVT模型中Tu大小的选择，参考历史经验Tu应设定为50。对于次一日的VaR进行测度，MONTE CARLO的模拟次数MC设定为100000。同样在NGARCH(正态分布)以及NHARCH(t分布)的模型参数下，获得到相应的次一日的VaR。同时历史模拟法及加权历史模拟法这两种非参数度量方法，也能估计次一日的VaR值。在得到次一日VaR之后，便能够对未来一日的风险进行有效的管理。

综上所述，各方法在1%、5%置信度下的次一日VaR预测结果见表4。

表3 NGARCH不同假设下测度效果

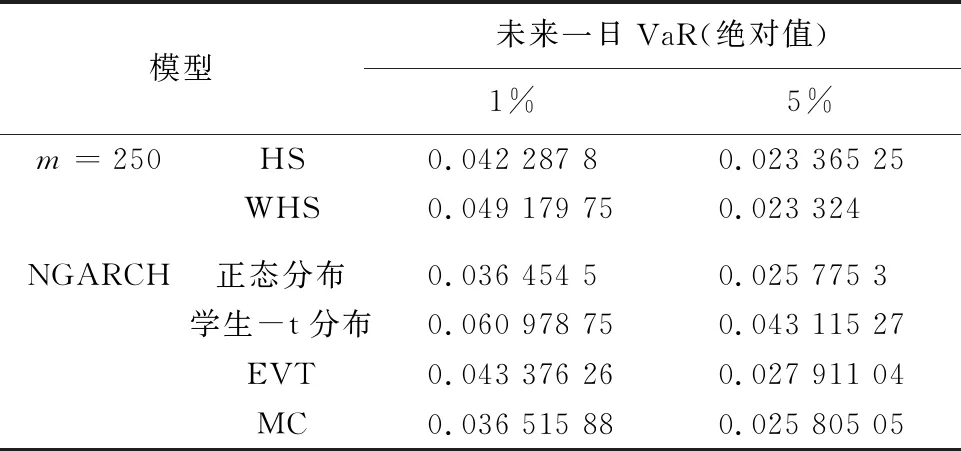
表4 不同模型下次一日VaR预测

4 结束语

通过运用非参数法、参数法对VaR进行测度结果表明：针对VaR的计算，参数法中加权历史模拟法，准确性更高，更具有实际意义，是一种更适合VaR的风险测度的方法。其次，尽管金融数据具有尖峰厚尾的情况，但通过使用沪深300指数，对于该指数收益率的测度后发现，NGARCH模型正态分布假设下的VaR效果优于t分布。t分布下对于VaR的预测过于保守，会导致投资者的资金的持有成本较高，不利于投资者资金的流动以及操作灵活性。因此，在计算VaR的参数法上，可以采用正态分布假设下的NGARCH模型。在EVT、MONTE-CARLO对于金融数据的模拟同样有效的基础上，通过分别将此两种测度方法与NGARCH模型结合，进一步通过提出并使用GARCH-EVT MONTE-CARLO-GARCH的新方法，对次一日的VAR进行预测，均得到了VaR相应的结果，说明这二种方法都可以对金融风险进行预测并效果显著。在预测次一日VaR的结果上，GARCH-EVT 、MONTE-CARLO-GARCH模型与2种历史模拟法、正态分布及学生t分布下的NGARCH模型综合对比，得到次一日的VAR风险值，给予投资者预测投资信息以及投资风险警示。本文对于VaR的测度进行了相应的扩展，为今后的VaR的准确性以及资金的持有，提供了具有更高把握的方法，对于将来的VaR测度有了更好的理论支持以及发展前景。