关于概率论在生活中的应用探讨

简艺

【摘要】概率论是对随机现象统计规律演绎的研究，它的一些原理和知识普遍应用于生活的点点滴滴，如生活中的抓阄问题、福利彩票的中奖问题、赌博时赌注的合理分配问题等.基于对这些问题的认识，文章从概率论的角度出发，结合具体的事例，对生活中的概率问题进行了探讨.

【关键词】概率论;条件概率;古典概型;贝叶斯公式;数学期望

【基金项目】广东茂名幼儿师范专科学校2020年度教育科学“十三五”规划课题——新版课程标准和教资国考背景下的《小学数学课程与教学》的课程设计与教材建设（2020GMYSKT02）

概率论是研究随机现象数量规律的一门重要的数学分支，它源于生活，也用于生活.随着科学技术的发展以及计算机的普及，概率论不仅被广泛用于各行各业，为分析社会现象、研究自然科学、处理公共事业提供了极大的帮助，在生活中也发挥着越来越广泛的作用.事实证明，生活中处处存在着概率，而且生活中的概率问题往往让我们意想不到.那么怎样学会运用概率知识来解决生活中的简单实际问题呢？下面结合本人多年的教学实践谈谈概率论在生活中的一些简单应用.

一、彩票问题

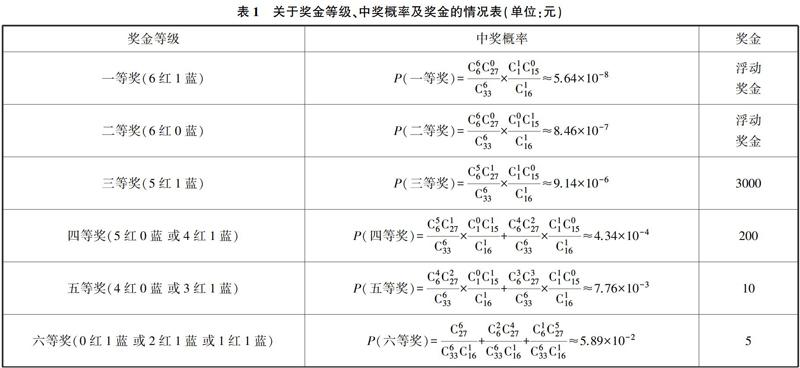
双色球彩票是中国福利彩票的一种，开奖规则是从33个红色球中选6个再加上从16个蓝色球中选1个，一共7个数字组成一注.开奖后按号码重合个数决定奖金等级，这其中是不论顺序的，号码对了即可.奖金等级分为一、二、三、四、五、六等奖：一等奖 6红1蓝，浮动奖金;二等奖6红0蓝，浮动奖金;三等奖5红1蓝，3000元;四等奖5红0蓝或4红1蓝，200元;五等奖4红0蓝或3红1蓝，10元;六等奖0红1蓝或2红1蓝或1红1蓝，5元.浮动奖金是根据当期的销售情况来定的，如2010年一、二等奖的奖金平均值分别为696万元、23.4万元.

根据上表容易算出双色球的总中奖率P≈0.067，说明100人各买一注的话，约有6人会中奖.由于中五等奖的概率为7.76×10-3<0.01，故中五等奖是一个小概率事件，根据小概率事件原理知道，小概率事件在一次实验中一般不会发生，只有在大量实验后方可发生.所以一般情况下你买的少量几注彩票是不会中奖的.

那么当你拿出2元买一注彩票时，你获利的期望值是多少呢？下面以2010年的浮动奖金计算如下：

5.64×10^-8×6960000+8.46×10^-7×234000+9.14×10^-6×3000+4.34×10^-4×200+7.76×10^-3×10+5.89×10^-2×5+（1-0.067）×（-2）≈-0.789.

即买一注彩票获利的期望值为 -0.789元，说明我们每买一注双色球彩票平均损失0.789元，买得越多越逃不出这个宿命，所以福彩中心永远是赢家.如果三、四、五、六等奖奖金不变，要想获利期望值为零，也就是不赚不亏，那么一等奖奖金要定位为16251600元，二等奖奖金要为546390元.而福彩中心已经明文规定一等奖奖金不超过一千万，这样才会保住他们募集福利资金的宗旨.

二、抓阄问题

在生活中，我们经常会遇到一些抓阄、抽签的问题，有人会想到先抽者有利，正所谓“先下手为强”，但是真的是这样吗？ 下面我们先解决如下问题.

例1 n个人用摸彩的方式决定谁得到一张电影票，他们依次摸彩，求第k（k≤n）个人摸到电影票的概率.

分析 这是一个条件概率问题，第k个人摸到，说明前（k-1）个人都没有摸到，第二人摸时是在第一人没摸到的条件下进行的，同样第三人摸时是在第一和第二人同时没摸到的条件下进行的，以此类推.

解 令Ai=“第i个人摸到票”，i=1，2，3，…，（k-1），k，第k个人摸到，说明前（k-1）个人都没有摸到，故第k人摸到的概率为

P[ZK（]=P（A1A2…Ak-1Ak）=[ZK（]P（A1）P（A2A1）P（A3A1A2）…

P（Ak-1A1A2…Ak-2）P（AkA1A2…Ak-1）[ZK）]=n-1n×n-2n-1×n-3n-2×…×n-（k-1）n-（k-2）×1n-（k-1）=1n，[ZK）]

可見每个人摸到电影票的概率都是一样的，与摸的顺序无关.

一般地，有下列结论：若n个签中有m（1

三、生日问题

例2 著名生日问题：从一个较大的人群中随机地选取n（n≤365）个人，求其中至少有两个人的生日相同的概率.

分析 两人的生日相同是指两人出生于一年内的同一天，如果排除主观因素，认为生产是自然现象，即每个孩子在哪天出生都是等可能的，本题是一个古典概型问题.

解 设A=“n人中至少有两人生日相同”，则A-=“n人中没有两人生日相同”，假定一年以365天计算，一个人的生日可以是365天中的任一天，即有365种情况，故n 个人的生日情况包含365n个基本事件.

n个人中没有两人同一天生日，就相当于从365天中任意选出n天的排列，即含Cn365·n！个基本事件，故有

P（A-）=Cn365·n！365n=365！365n（365-n）！，

所以

P（A）=1-P（A-）=1-365！365n（365-n）！.

当n较大时，上式计算量很大，下表列出一些具体数值：

从上表容易看出，一个有50个学生组成的班集体，至少有两人生日相同的可能性竟然高达97%，这是难以想象的.

四、比赛问题

乒乓球比赛规则有3赛2胜制、5赛3胜制和7赛4胜制等，在实战中选择哪种规则对自己更有利，选择哪种规则对参赛双方较为公平，这些问题都是参赛者和组织者关注的问题.

例3 甲、乙两乒乓球运动员在一场比赛中，甲胜的概率为0.52，乙胜的概率为0.48.试计算3赛2胜制和5赛3胜制哪个对甲更有利.（假设3赛2胜制和5赛3胜制分别打完3场和5场）

解 令A=“一场比赛，甲胜”，

则P（A）=0.52，P（A-）=0.48.

（1）对于3赛2胜制：可以看作是n=3的独立重复试验，此时甲胜的概率为

P3（m≥2）=C23×0.522×0.481+C33×0.523=0.529984.

（2）对于5赛3胜制：可以看作是n=5的独立重复试验，此时甲胜的概率为：

P5（m≥3）[ZK（]=C35×0.523×0.482+C45×0.524×0.48+C55×0.525≈0.537460.[ZK）]可见P5（m≥3）>P3（m≥2），即5赛3胜制对甲更有利.

这表明，如果本方每局获胜的概率比对方的概率大，那么多比赛几局对本方来说是有利的.但从公平的角度而言，3赛2胜制比5赛3胜制更公平、合理.

五、合理分配赌注问题：

2002年中央电视台第10频道与观众互动节目中有这样的一个题目：

例4 甲、乙两人各出赌资5个金币，形成10个金币的赌资.规定最先赢得5局的人获胜.现在进行了7局，甲赢了4局，乙赢了3局，因故不得不终止比赛.问：这些赌资应如何分配？

当时问了演播厅的三位观众，都说按47和37分配合理.

事实上，从概率论的角度思考，两人在每一局获胜的概率都一样，即12.

现假定再比赛一局（第8局）.

甲的形勢是：若甲赢了第8局，则得到全部10个金币，但赢的概率是12，所以期望值是5个金币;若甲输了，那么甲、乙打平，甲得5个金币，但输掉的概率也是12，故期望值是2.5个金币.合计共得7.5个金币.

乙的形势是：若乙赢了第8局，则得到5个金币，但赢的概率是12，故期望值是2.5个金币;若是输了，则得到0个金币.

解 令ξ表示第8局结束后甲能得到的金币数，由于甲输赢的概率都是12，赢了ξ=10，输了ξ=5，即ξ服从的分布表为：

令η表示第8局结束后乙能得到的金币数，由于乙输赢的概率都是12，赢了η=5，输了η=0，即η服从的分布表为：

故ξ与η的数学期望分别为：10×12+5×12=7.5，5×12+0×12=2.5.

即甲、乙两人应分别得到7.5个金币和2.5个金币.

这是帕斯卡分配赌金的故事，最早于1494年由意大利数学家帕乔利提出，16世纪中期的卡尔达诺和塔尔塔利亚等人也讨论过这类问题.17世纪中叶法国人梅雷向数学家帕斯卡重提这类问题，引起帕斯卡与另一位数学家费马在1654年7月至10月间的通信讨论，数学史上称这些通信为最早的概率论文献.

六、追究责任问题

现实生活中经常会遇到一些责任问题，这些问题追究起来往往是比较麻烦的，正所谓“公说公有理，婆说婆有理”.如何合理地解决这些问题？笔者认为这些问题大多属于逆概率问题，也就是说现在是问题出现了（即某事件已经发生），在这样条件下，如果能计算出各方参与这件事的概率有多大，问题便可解决.

例5 仓库有10000个产品，分别为甲厂5000个，乙厂3000个，丙厂2000个，次品率分别为1%，2%和0.5%.

（1）求仓库里全部产品的次品率;

（2）若仓库规定：生产了次品要追究工厂的经济责任.现在在仓库中任取一个产品，结果为不合格，但这个产品是哪个工厂生产的标志已经脱落，问：仓库该如何处理这个产品比较合理？甲、乙、丙分别应承担多大的经济责任？

解 （1）令A=“任取一个为次品”，B1=“任取一个为甲厂产品”，B2=“任取一个为乙厂产品”，B3=“任取一个为丙厂产品”.

（2）从概率论的角度考虑，按概率P（Bi|A）的大小来追究工厂的经济责任较为合理，而

可见乙厂责任较大，丙厂责任较小.如果说要罚款10000元，那么甲、乙、丙分别应承担4170元、5000元和830元才合理.

P（Bi|A）=P（Bi）P（A|Bi）P（A）（i=1，2，…，n）叫作贝叶斯公式（也叫逆概率公式），其中P（Bi）叫作先验概率，是长期经验知道的结果，而P（Bi|A）叫作后验概率，是医生常用的结论.这公式是英国医生贝叶斯发现的，最初用于医学的疾病诊断，现在被广泛应用于市场预测、安全监控等.

上述仅从生活的角度探讨了概率知识在人们生活中的一些简单应用，事实上，概率论在自然科学、社会科学、工程技术、军事科学及农业生产等领域都有着不可缺少的作用.直观地说，卫星上天、导弹巡航、飞机制造、宇宙飞船遨游太空等都有概率论的一份功劳.概率论作为理论严谨、应用广泛的数学分支正日益受到人们的重视，并将随着科学技术的发展而发展.

【参考文献】

[1]吴志高，王群，朱成杰.统计与概率[M].北京：高等教育出版社，1996.

[2]章德.概率论与数理统计[M].北京：北京航空航天大学出版社，2003.

[3]毛纲源.概率论与数理统计解题方法技巧归纳[M].武汉：华中科技大学出版社，1999.