基于碎片化学习的数学建模课堂教学研究
胡文燕

【摘要】《数学建模》是各高校数学专业的一门课程,一直以来深受广大师生关注,但在课堂教学中却存在着诸多问题.为充分调动学生主动学习,更快更好地提高线上线下相结合的混合式课堂教学的灵活性和教学效果,文章通过对数学建模过程中的模型假设、模型建立、模型求解进行探讨,结合实践教学经验,将碎片化学习理念融入实际课堂教学中,并通过建模案例给出几点教学建议.
【关键词】碎片化;关键词;建模目的;求解方法
【基金项目】山西省教育科学“十三五”规划课题资助项目(GH-16107);晋中学院教学改革与研究项目(Jg201914);晋中学院“数学建模”优秀教学团队资助项目;山西省高等学校教学改革创新项目(J2020319)
一、引 言
数学是一门基础学科,它可以迅速地發展并渗透到各个新的专业和领域,为不同专业和领域的实际应用和问题研究提供合理有效的解决方案和解决方法,几乎所有问题、所有课题的解决都离不开数学建模[1].但在实际教学中,却存在着很多问题,学生对建模方法的掌握往往不够透彻,有很多学生会觉得数学建模课程不像其他专业课程那样系统,各章节之间也没有承上启下,环环相扣,而是整体表现得零零碎碎,相互独立[2].
2020年初,突如其来的疫情打乱了各高校、各行业的既定步伐,为切实确保各高校全体师生的生命安全和学生的身体健康,各高校多次推迟了开学.在此期间,本着“停课不停教、停课不停学”的原则,各专业、各学科根据各自的专业特点,积极实行了线上网络课堂教学.
与传统教学相比,线上教学更加彰显了学生的主体地位,而学生对线上教学的态度,直接影响到教学成效.线上教学更需要学生积极主动思考,自主查阅资料,分组研讨,这也就要求学生投入大量的时间和精力.那么,如何充分引导全体学生发自肺腑地自主参与学习,如何充分调动全体学生的自主学习兴趣和主动性就迫在眉睫,这也是研究性教学必须认真考虑的主要因素和问题.
二、数学建模课堂的教学探讨
为了有效提高数学建模课程的实用性和教学效果,引导全体学生主动参与学习,只有从最根本的角度出发,让全体学生真正掌握数学建模的基本方法,一切困难才能迎刃而解,这就要求教师在课堂讲授的过程中,面对无从下手的问题,适时引导学生巧妙结合数学模型来自实际又有别于实际这个特性,将实际问题碎片化[3],再一一击破,最终找到建模过程中模型假设、模型建立及模型求解的突破点,并构建合理的数学模型.
(一)“关键词”在模型假设中的作用
众所周知,模型假设在整个建模过程中起着至关重要的作用,模型假设的必要和合理程度,直接关系到建模的成败.[4]但在许多实际问题的建模过程中,学生往往是一头雾水,尤其面对看似简单的开放性题目,更是一筹莫展,无从下手.为了消除学生心中这种困惑,使他们面对实际问题能够充分发挥想象力,给出合理全面的简化假设,教师可以引导学生挖掘题目,将所给题目碎片化,找出题目语句中的所有关键词,并针对关键词逐个研究,结合题目中所给的实际问题,一一给出适当合理的假设.
现在以模型“椅子能在不平的地面上放稳吗?[5]”和模型“双层玻璃窗的功效[5]”为例具体阐述.
1.以“椅子能在不平的地面上放稳吗?”为例
该问题只有短短几个字,这会令大部分学生陷入迷茫,不知从何处下手,此时可将其关键词一一列出,并逐一给出合理的简化假设.
首先,“椅子”是这句话中的主语,是当之无愧的关键词.生活中的椅子多种多样,无论是材质还是形状都各有不同,但若想建立数学模型解决这个问题,就必须对“椅子”做出明确、具体的假设.由题目所指,其关注的是椅子能否放稳的问题,故重点在于椅脚,而对椅面的形状却不必要求.结合实际情况,日常生活中的椅子大多是四条腿的,为简单起见,可假设椅子有四条腿,并将椅子四条腿的长度看成完全一样的.若将椅脚与地面接触处视为一个点,并取规则的平面中心对称图形——正方形作为椅脚连线所构成的图形,就可以巧妙地将“椅子”与“正方形”联系起来,将实际问题用数学语言描述出来.
其次,“不平的地面”也是五花八门、各种各样,甚至会有台阶这样的情况出现.秉承合理简单的原则,可将地面高度看成连续变化的,沿任何方向都不会出现断裂,从而可将“不平的地面”视为数学上的连续曲面,并且它是相对平坦的.
最后,“放稳”这个关键词是该问题的关键,为了能借助数学工具证明椅子能否在不平的地面上放稳,就必须用数学语言来描述“放稳”这个特征.因为当椅子稳稳地放在地面上时,其四只椅脚都是紧紧着地的,所以,可先假设椅子的椅脚只有三只脚同时着地,这样就大大简化了问题,并使得问题更加明朗.
2.以“双层玻璃窗的功效”为例
乍一看这个题目不像是一个问题,不同于上一个模型是用问句呈现的,此处更像是一个标题.但其实不难想到,这个模型是要研究我们日常生活中常见的双层玻璃窗的功效如何.
同前一个模型一样,大部分同学会一头雾水,不知道从哪里入手,这就需要我们一一找出关键词,逐个攻破.
这里有三个“关键词”:“双层”“玻璃窗”和“功效”.先来看“双层”:现实生活中,北方大部分城市建筑物的窗户都是双层玻璃的,也就是说窗户上装有两层玻璃.细心观察,会发现这两层玻璃并不是紧紧挨在一起的,它们中间有一定的空隙.那么,这个空隙中有什么呢?毋庸置疑,是空气.清楚双层玻璃窗的结构以后,就要求我们在模型假设时,必须考虑双层玻璃之间的距离,距离的选择一定是最终玻璃窗功效的必要因素.
再看第二个关键词“玻璃窗”:玻璃窗的安设目的是保暖,而市场上的玻璃五花八门,品种烦多,玻璃的材质不同,厚度不同,其保暖效果自然也就不同.那么,如何选择玻璃,玻璃的材质、材质均匀程度和厚度对保暖效果又起到了多大的作用,都是我们需要研究的因素.
最后一个关键词“功效”:指的是保暖效果到底有多好.结合物理学的知识我们知道,想要了解玻璃窗能多大程度的保暖,就是要研究热量是如何在室内有取暖措施的情况下,通过玻璃窗流失的,这就涉及了物理学中热量传导的问题.制作工艺不同的玻璃,其各个点的热传导系数也不同,为简单计,我们假设玻璃窗的玻璃材料均匀,热传导系数是常数.因为双层玻璃窗不仅有玻璃,还有空气,所以我们除了要研究玻璃的热传导以外,还必须考虑热量通过空气的传导.
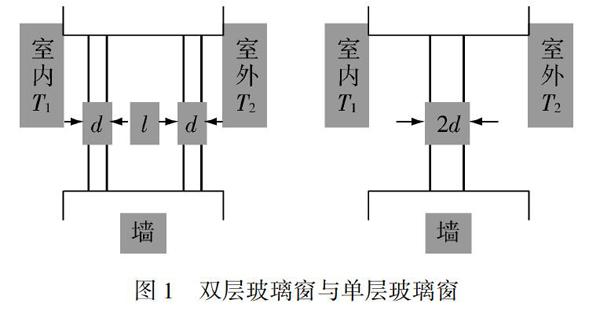
为了更好地突显双层玻璃窗的功效显著,我们可以将其与单层玻璃窗进行比较,用数据说话.为了公平起见,可设单层玻璃窗的玻璃厚度是双层玻璃窗玻璃厚度d的2倍,如图1:
我们假设,双层玻璃窗中间所夹空气的厚度为l,为简单计,假设窗户的密闭性很好,两层玻璃之间所夹的空气是不流动的,也就是说,此处热量的传播过程只有传导,没有对流;室内、室外温度分别为T1,T2,热传导已经处于稳定状态,室内、室外温度保持不变.这样我们就顺利地从三个“关键词”入手,合理地对原问题进行了简化,巧妙地将其用数学语言描述了出来.
(二)建模目的是模型构建的切入點
对问题有了合理的假设后,就需根据对象的内在规律建立数学模型,但在实际教学中,学生经验不够丰富,知识储备不够充足,往往不知从哪里入手,这就需要教师从模型建立的目的出发,一点一点引导,带领学生找到模型建立的切入点.仍以模型“椅子能在不平的地面上放稳吗?”和模型“双层玻璃窗的功效”为例.
第一个模型“椅子能在不平的地面上放稳吗?”中,“放稳”的意思可以很简单地理解为椅子的四只椅脚同时着地,也就是四只椅脚与地面的距离都为零.而椅脚与地面的距离恰恰与椅子的位置有关,若我们能用正确的数学语言准确地描述椅子的位置,那么就说明我们可以把“椅子四只脚同时着地”的所有条件和所得出的结论都用正确的数学语言准确地表示了出来.
注意到椅脚连线呈正方形,而正方形是一个中心对称图形,当椅子位置发生改变时,正方形绕其中心旋转的角度正好代表了椅子位置的改变,那么我们就可以用位置变量θ来描述椅子的位置.进一步地,可假设A,C两脚与地面距离之和为f(θ),B,D两脚与地面距离之和为g(θ),这样我们就找到了模型建立的关键——数量指标,从而构建该实际问题的数学模型就变得非常容易了.
这个模型的巧妙之处就在于用变量θ表示椅子的位置,用θ的两个函数表示四脚与地面的距离,而这都得益于对模型建立的目的这个切入点的分析研究.
第二个模型“双层玻璃窗的功效”中,建模目的是通过比较单层玻璃窗和双层玻璃窗的热量流失,研究双层玻璃窗的“功效”.
热传导过程遵循物理学中的物理定律:厚度为d的均匀介质,两侧温度差为ΔT,则单位时间由温度高的一侧向温度低的一侧通过单位面积的热量Q与ΔT成正比,与d成反比,即
Q=k(ΔT/d).
接下来只需要分别求出双层玻璃窗和单层玻璃窗各自单位时间通过单位面积的热量,并进行比较即可.虽然一个房间的热量流失不仅仅通过玻璃窗,还可以通过天花板、地面、墙壁等介质流失,但这个模型已经足够证明双层玻璃窗确实比单层玻璃窗在保暖方面更胜一筹,功效显著.
由此可见,教会学生如何从建模目的出发找到模型构建的切入点是何等重要.
(三) 模型求解方法的选择
数学模型的形式多种多样,或者是数学公式、图表、微分方程组,或者是一种算法,不同类型、不同形式的数学模型有着各自不同的求解方法,但也有一类数学模型,虽然模型形式相同,但有的模型变量特征不同,有的模型变量个数不同,有的模型建模目的不同,这时它们的求解方法也截然不同.
1.微分方程模型的求解
微分方程模型[5]是一类描述实际对象随时间(或空间)演变过程,分析其变化规律,预测其未来性态的动态模型.经典的指数增长模型(Malthus模型)和阻滞增长模型(Logistic模型)都是以微分方程形式呈现的.
其中,x(t)为t时刻的人口,r为人口的固有增长率,xm为环境所能容纳的最大人口数量.
这两个模型构建的目的都是为预测t时刻人口的数量,故模型求解均是直接求微分方程的解,以此来预测人口.
但还有一类模型,虽也是以微分方程形式呈现的,但求解方法却大不相同.以模型“种群的相互竞争[5]”为例,我们假设甲、乙两个种群在各自独立生存时,都遵从Logistic规律,那么t时刻两种群的数量x1(t),x2(t)满足:
其中r1,r2分别为甲、乙两个种群的固有增长率,N1,N2是最大容量,单位数量的乙(甲)种群消耗供给甲(乙)种群的食物数量是单位数量的甲(乙)种群消耗供给乙(甲)种群的食物数量的σ1(σ2) 倍.
这个模型与Malthus模型及Logistic模型相比,形式是一样的,都是微分方程,但因为该模型构建的目的是若干年后两个相互竞争种群的演变结局,所以在对该模型进行求解时,并不需要直接对微分方程进行求解,而是运用微分方程的稳定性理论,直接研究其平衡状态的稳定性,这也大大简化了模型的求解.
由此可见,即便模型的形式是一样的,但若是建模的目的不同,求解方法也是大不相同的.
2.数学规划模型的求解
数学规划模型[5]是一类优化模型,建立优化模型需要确定优化的目标和寻求的决策.实际生活中,很多问题归结出的优化模型,其决策变量个数和约束条件个数一般都比较大,这样就不能简单地用微分法求解,需要用到数学规划的方法.本文就典型的数学规划模型——运输问题和指派问题进行研究,探讨其模型求解方法的不同.
运输问题是线性规划应用最广泛的领域之一,以产销平衡运输问题为例,其数学模型形式如下:
该模型虽是一个线性规划模型,但其结构却具有特殊性,它含有m×n个变量,(m+n)个约束,约束条件系数矩阵的元素都等于0或1,模型的变量和约束均较多,故不适合用常规求解线性规划模型的单纯方法求解,而采用表上作业法求解这一类产销平衡的运输问题.
进一步,如果所有的决策变量不再仅仅是非负约束,而是0-1变量,又有模型中m=n,此时上述模型可写为:
很显然,这是典型的指派问题,它是一种特殊的平衡运输问题,此处可将每个生产地的产量和每个销售地的销量都看作1,由于其结构的特殊性,不再用表上作业法,可用更为简便的匈牙利算法进行求解.
再有,如果约束条件不全是等式,m≠n,建立0-1规划模型是常用方法,由于任务的数量与能够承担的人员数量不一定相等,约束条件不再都是等式约束,故匈牙利算法不再适用,我们可以选择Lingo数学软件对其进行求解.
综合上述,同样都是数学规划模型,如果变量个数不同,类型不同,或者约束条件不同,那么即便其形式很相似,求解方法也截然不同.这就要求教师在课堂教学中针对不同的数学模型,详尽分析其模型形式,建模目的的异同,从而选取适合的求解方法.
三、 结 语
数学建模的教学一直是备受关注的重要课题,为了真正地将建模方法教给学生,教给学生如何真正地借助数学工具解决实际问题,就一定要认真钻研教材、研究教法,从提高学生学习主动性出发,将碎片化教学理念巧妙融入实践教学中,线上线下相结合,真正提高教学质量.
【参考文献】
[1]唐娅娴.数学建模思想对大学生数学应用能力的影响[J].科技经济导刊,2017(8):160.
[2]尹裴,关晓飞.数学建模课程教学实践研究[J].教育教学论坛,2016(37):75-76.
[3]郭亚娜,丁振国,李尚富.探究“碎片化”教学资源设计原则与建设 [J].科技展望,2016(35):161-162.
[4]赵建昕.提高数学建模能力的策略研究[J].数学教育学报,2004,13(3):50-51.
[5]姜启源.数学模型:第四版[M].北京:高等教育出版社,2011.

