2019年全国高考数学试题的物理之问

褚华

摘   要：2019年全国高考数学II卷的一道以天体运动素材做背景的数学试题，通过物理之问，进行了物理方面的分析，让大家了解拉格朗日点的由来，以及它对未来深度空间探测的意义;介绍了中继星“鹊桥”在登月过程中的作用。

关键词：拉格朗日点;深度空间;高考试题

中图分类号：G633.7 文献标识码：A    文章编号：1003-6148（2020）1-0043-3

2019年全国高考数学I卷的“断臂维纳斯”和数学III卷的“一朵云”瞬间成为网红高考试题，成为人们热议的高考话题。其实，在全国数学II卷中，还有一道让物理老师拍手叫绝的好题，就是全国高考数学II卷中的第4题，是以天体运动为背景的空间几何体的基本运算数学考题。试题以我国最新的空间技术成就“2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆”为背景，融合数学上的拉格朗日点概念，巧妙地设置了一道空间几何关系的运算数学高考试题，让人耳目一新。按理说，像这样的最新航天技术的素材，作为高考物理试题的背景材料是最好不过的了，但没想到被今年的高考数学试题捷足先登。

1    高考数学原题

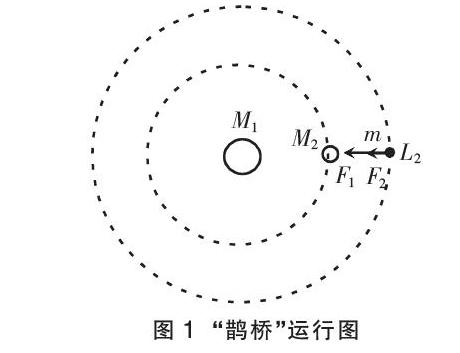
2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆，我国航天事业取得又一重大成就，实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系。为解决这个问题，发射了嫦娥四号中继星“鹊桥”，鹊桥沿着围绕地月拉格朗日点L2的轨道运行。L2点是平衡点，位于地月连线的延长线上。设地球质量为M1，月球质量为M2，地月距离为R，L2点到月球的距离为r，根据牛顿运动定律和万有引力定律，r满足方程：

正确选项：D选项。

此题看似像物理题，却并没有考查物理方面的知识内容，仅仅从运算的角度，考查学生在物理情境下的数学运算能力。这种运算过程与难度在高考数学试题中应属于中等难度，其实在很多高考物理试题中也是常见的。

3    物理之问

3.1    第一问——数学试题中给出的+=（R+r）关系式是如何得到的

如图1所示，嫦娥四号中继星“鹊桥”绕地球运动的向心力来源于地球和月球对它的万有引力，且运动的角速度与月球绕地球运动的角速度相同，设为ω，分别对“鹊桥”和月球列方程如下：

3.2    第二问——拉格朗日点的由来

1687年，牛顿发现万有引力，并提出万有引力公式。人们应用万有引力定律很容易算出宇宙中两个天体在引力作用下的运动情况，得到天体的运动轨道。但是，有第三个天体存在的话，情况就会变得异常复杂，不可求解。这便是著名的三体问题。

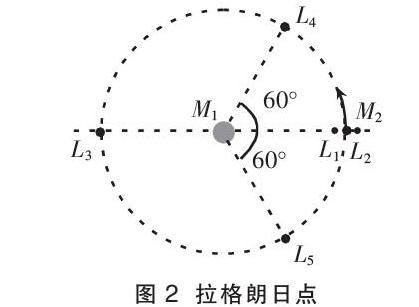
针对复杂的三体问题，数学家先着手进行简化，比如其中一个天体的质量非常小，变成了限制性三体问题，求解也变得简单很多。1767年数学家欧拉根据旋转的二体引力场推算出其中三个点（特解）为L1、L2、L3。1772年数学家拉格朗日把“限制性三体问题”进一步简化为“平面圆形限制三体问题”，并推算出了另外两个点（特解）为L4、L5，如图2所示。人们把L1、L2、L3、L4、L5叫做拉格朗日点。其中，物体在L1、L2、L3三个点的位置上是不稳定的，受稍微的扰动就离去而不再复位;在L4、L5两个点上是稳定的，受到扰动后不会离去，而是在这个点附近往复运动。

1906年，天文学家沃尔夫，发现了一颗行为怪异的小行星，它的绕日轨道与木星完全相同，在木星前方运行。看上去，小行星、木星、太阳三者总是呈等边三角形，这颗小行星被命名为“阿基里斯”。科学家很快意识到，这或许就是拉格朗日点存在的证据。很快，天文学家又在相反的位置上，也發现了小行星，后来还发现了大量的小行星，存在于这两个点上。这也是科学史上先在理论上预言，然后又在实际观察中发现得到证实的生动事例。

拉格朗日点的物理意义：在由两个质量较大的天体M1、M2构成的系统中，都存在5个拉格朗日点。在这些点处，放入第三个物体（质量忽略不计），它在天体M1、M2的引力作用下，相对于M1、M2基本上保持相对静止（即运转角速度和周期相同）。

3.3    第三问——题根在哪里

其实，今年的全国数学II卷中的这道以“拉格朗日点”为素材的数学试题，也并非是一道创新之作，它源于高中物理竞赛试题，是对第32届（2015年）全国中学生物理竞赛预赛试卷中一道试题的改编。

竞赛试题：2011年8月中国发射的宇宙飞船“嫦娥二号”在完成探月任务后，首次从绕月轨道飞向日地延长线上的拉格朗日点，在该点，“嫦娥二号”和地球一起同步绕太阳做圆周运动。已知太阳和地球的质量分别为MS和ME， 日地距离为R。该拉格朗日点离地球的距离x满足的方程为        ，由此解得

显然，物理竞赛题的第二填空对学生的数学运算能力的要求，高于2019年全国高考数学II卷第4题对学生数学运算能力的要求。

竞赛试题是以日地拉格朗日点为背景材料，高考数学题是以地月为背景材料，如出一辙，本质上是同一个物理模型。数学题中的月球到L2的距离与物理竞赛试题中的地球到L2的距离数学表达形式完全相同。

3.4    第四问——拉格朗日点在深空探测技术上的意义

拉格朗日点又称平动点，日地系统、地月系统均存在五个拉格朗日点。如果在这些点上放置信息中继探测器、卫星或空间站等，可以建立一个相对日地系统或地月系统稳定的深空探测环境或通信节点。除此之外，中继探测器、卫星或空间站处在拉格朗日点上所消耗的燃料非常小。

人类从1978年第一颗拉格朗日点卫星国际探测者三号发射成功开始，拉开了拉格朗日点开发利用的序幕。近年来，拉格朗日点的应用已成为国际空间探测的热点，多颗该类卫星相继发射成功。如1995年12月2日用“宇宙神”运载火箭从卡拉维纳尔角发射的太阳与日光层观测台探测器，在拉格朗日点L1附近运行，最初计划运行2年，实际上完成初始任务后继续执行扩展任务，目前探测器仍在轨运行中;2001年升空的威尔金森宇宙微波各向异性探测卫星（WMAP）;2009年欧洲航天局两颗科学探测卫星“赫歇尔”和“普朗克”也被定位在日地系统的拉格朗日点L2附近。

众所周知，哈勃望远镜的接班者——詹姆斯·韦伯太空望远镜，就将放置在太阳和地球的拉格朗日点（L2）处。哈勃望远镜与詹姆斯·韦伯太空望远镜的最大区别就是哈勃望远镜是围绕地球转，而詹姆斯·韦伯太空望远镜处在日地系统的拉格朗日点L2上绕太阳转。在距离我们150万公里的深空，远比距离地表600公里的哈勃望远镜遥远得多。该点永久背对着地球，引力场相对稳定，也没有近地轨道的尘埃和垃圾影响，具有超好的观测位置和视野。美国国家航空航天局计划于2021年发射哈勃望远镜的接班者詹姆斯·韦伯太空望远镜。

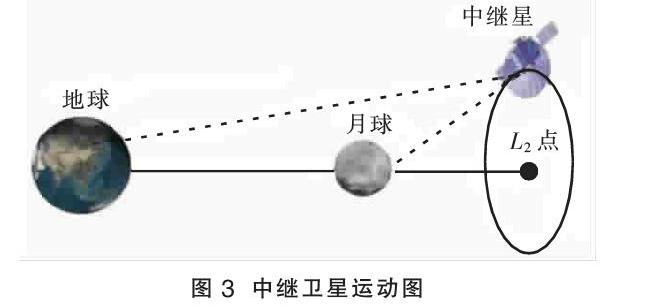
我国于2018年4月24日，成功將嫦娥四号月球探测器的中继卫星“鹊桥”号发射升空。“鹊桥”号并不是围绕月球旋转，而是围绕着地月系统的拉格朗日点L2旋转。为2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆提供了信息传送，如图3所示。

不论日地系统的拉格朗日点，还是地月系统的拉格朗日点，对于深空探测而言，都是稀缺资源。谁先占领拉格朗日点，不仅反映这个国家的科技水平，更是抢占了未来深空探测的主动权。拉格朗日点除了用于科学研究之外，还有极其重要的军事战略用途。它可以用于在轨备用卫星的停靠点，也可用来抵抗外层轨道发射的反卫星空间武器，比如用于抵抗地球同步卫星等。所以，在未来各国的太空计划中，围绕着拉格朗日点将会展开激烈的太空资源争夺战。

参考文献：

[1]李广侠，姜勇，孙玉华.拉格朗日点在深空通信中的应用[J].数字通讯世界，2011（1）：84-87.

[2]翟麓.迷人的“拉格朗日点”[J].太空探究，2011（11）：20-21.

[3]秦德胜.关于拉格朗日点的一道高考题[J].物理教学，2011，33（4）：71-73.

（栏目编辑    陈  洁）