对一道高考函数压轴题的思路分析与推广

纪定春

(四川省成都市四川师范大学数学科学学院 610068)

一、试题呈现与评注

试题呈现(2010全国数学新课标理科卷第21题)设函数f(x)=ex-1-x-ax2．

(1)若a=0，求f(x)的单调区间；

(2)若当x≥0时f(x)≥0，求a的取值范围．

评注该试题结构简单、形式优美，蕴含丰富的知识考点．试题的解决思路宽广，可以为不同学习水平的学生提供更好的方法选择．试题具有高等数学中麦克劳林展开式的背景知识，同时也具有竞赛数学中的重要不等式(对数不等式)的身影．在解决方法上可以使用高等数学的知识(洛必达法则)，同时可以使用高中数学中导数的定义来解决．因此，该试题具有丰富的内涵和多样的解答方案，是一个值得研究的好试题．同类型的试题还有很多，如2013年全国新课标卷2理科21题；2018年新课标卷1第21题；2018年广东省二模考试卷第12题；2018年百校示范卷(二)第21题等.这些试题都与该试题有较高的关联性，因此，对该试题的思路探究是有价值的．由于问题(1)较为简单，此处重点对问题(2)进行思路分析和推广．

二、问题(2)的思路探究

1.直接法

思路分析最直接的方式，就是将题干中的语言文字翻译成数学符号，然后利用导数来研究函数的最值或极值，此处需要求出f(x)的最小值都要等于零．

解析当x≥0时f(x)≥0，等价于f(x)=ex-1-x-ax2≥0，对任意的x≥0恒成立．对f(x)求导，可得f′(x)=ex-1-2ax，显然有f′(0)=0且f(0)=0．

因为g(x)=ex-1-x当x≥0时大于等于零恒成立，当且仅当x=0，g(x)=0．而f′(0)=0，得2a=1．当2a=1时，有f′(x)≥0成立．需要2a≤1，即a∈(-,就有f(x)≥0．所以a的取值范围为(-,

评注该方法充分地利用了重要不等式ex-1-x≥0，可以得出2a≤1．

2.换元构造导数定义法

思路分析该问题是一个恒成立问题，此处参数a分布简单，容易分离参数a，故可考虑分离参数．除了分离参数法，还可以移项变成恒成立问题，然后利用导数研究单调性和极值点，此处仅考虑分离参数法．

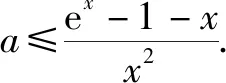
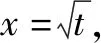
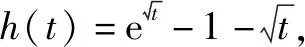
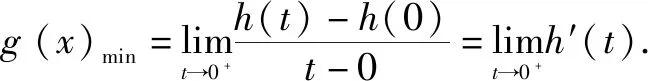
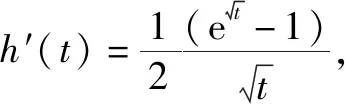
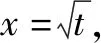
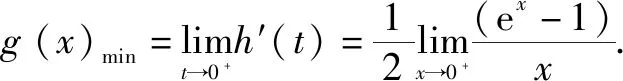
故a的取值范围为(-,

评注由此可见，对于分母为一个非一次单项式且极限为0时，通过换元法将高次的单项式变换为一次单项式，然后利用导数的定义来求解．同类型的试题还有，此处不再列出．

3.直接构造导数定义法

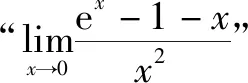
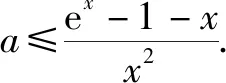
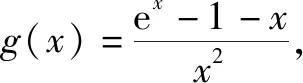
令函数m(x)=ex-1-x，n(x)=x2．

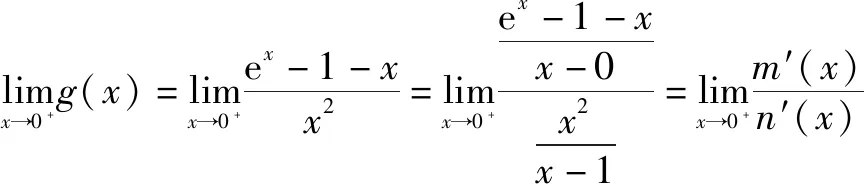
令函数p(x)=ex，显然p(0)=1．

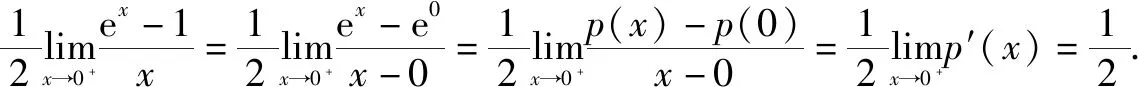
故a的取值范围为(-,

评注上述解法体现的是导数与洛必达法则之间的联系，高考中可以通过导数的定义来推导洛必达法则，这样就可以避免方法超前．

4.重要不等式法

思路分析对数不等式是一种重要的不等式，是高考数学中解决不等式问题的常用方法．证明方法较为简单，可以通过构造函数，然后利用导数来证明不等式恒成立．此处要证明函数f(x)=ex-1-x-ax2，当x≥0时有f(x)≥0成立，需要求a的取值范围．显然此处可以使用分离参数的方式，但是需要对自变量x进行分类讨论．

解析当x=0时，显然有f(x)=0，故f(x)≥0成立，此时有a∈R．

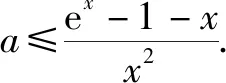
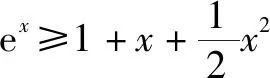
5.洛必达法则

思路分析分离参数之后，显然当中x→0时(x趋于0时)，该分式的分子和分母的极限值都是零，因此可以考虑使用洛必达法则．

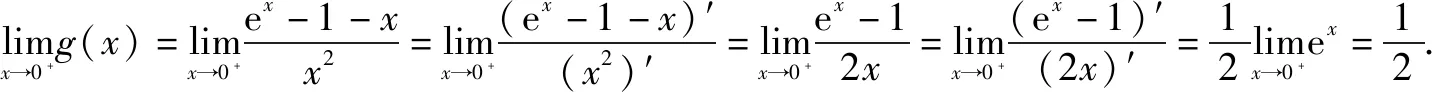
所以a的取值范围为(-,

评注可见，洛必达法则可以通过导数的定义来推导，这是一种更加高级的运算方式，但在使用洛必达法则时，一定要清楚使用的条件，而不是盲目的乱套公式．

6.等价替换法

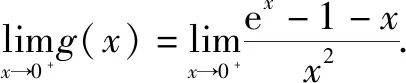
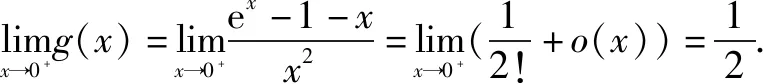
故a的取值范围为(-,

评注该方法是巧妙的运用了等价无穷小的知识，然后将截取的最高项次数控制为2，后面剩余项是关于的x无穷小量，故极限值为0．

三、问题的推广

问题是数学的心脏．好的数学问题、习题或试题，对培养学生的数学思维是有益的．好的数学问题是思路开阔和方法多样的问题，好的数学试题是可以推广的试题．接下来，将对原问题的问题(Ⅱ)进行推广，使其在更大的范围内也适用．

推广1若对任意x∈(-,+)，恒成立，求实数k的取值范围．

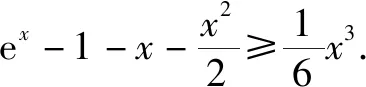
推广2若对任意x∈(-,+)，恒成立，求实数k的取值范围．

推广3若对任意x∈(0,+)，若不等式xex≥1+kx+lnx恒成立，求实数k的取值范围．

提示用xex=elnx·ex=ex+lnx≥1+x+lnx，当且仅当x+lnx=0时，等号成立．

推广4若对任意x∈(0,+)，若不等式xenx≥1+kx+lnx恒成立，求实数k的取值范围．

提示解决方法，同推广4．当且仅当nx+lnx=0时，等号成立．

推广5若对任意x∈(0,+)，若不等式xmex≥1+2kx+mlnx恒成立，求实数k的取值范围．

提示解决方法，同推广3．当且仅当x+mlnx=0时，等号成立．

推广6若对任意x∈(0,+)，若不等式xmenx≥1+kx+mlnx恒成立，求实数k的取值范围．

提示解决方法，将推广4、5结合起来． 当且仅当nx+mlnx=0时，等号成立．

以上推广，除了推广2较难以外，可根据学生的情况，将上述推广内容纳入课堂教学．