核心素养视野下学生数学弹性思维的培养

何正文

(广东省肇庆市百花中学 526000)

笔者认为数学核心素养指的并不是一项特定简单的数学能力,而是学生对于数学综合能力的一个集合.而弹性思维就是学生数学核心素养基本要素，并且，弹性思维作为核心素养的重要品质进行体现.数学弹性思维往往通过逆向形式，发散形式，类比形式，矛盾形式来进行深化核心素养.

一、在逆向形式上培养学生弹性思维

逆向形式也叫反向弹性思维，因为思维惯性的原因，学生往往习惯着单一僵化的思维方向思考问题.如果能引导学生从结果进行出发，层层回推，找寻条件和相关定理，往往思路更为清晰.从这种逆向形式上往往能在纵向提高学生数学核心素养，强化培养学生弹性思维长度.

例如：已知矩形ABCD，过A作SA⊥平面AC，过A作AE⊥SB交SB于E，过E作EF⊥SC交SC于F.求证：AF⊥SC.

思路AF⊥SC⟸SC⊥含AF的平面AEF⟸SC⊥EF,SC⊥AE⟸AE⊥含SC的平面SBC⟸AE⊥SB,AE⊥BC⟸BC⊥含AE的平面SAB⟸BC⊥AB,BC⊥SA.

上面的解法是由结论到条件的逆向求解.

首先我们发现AF与SC是两异面直线，要证明其垂直，往往要通过证明线面垂直，即证①AF⊥含SC的平面或证②SC⊥含AF的平面.因为题干中没有给出与AF有关的垂直条件，学生的思维转到证SC⊥含AF的平面AEF；继续逆向思考，逆向证SC⊥平面AEF，根据线面垂直的判定定理，即证SC⊥EF,SC⊥AE；已知SC⊥EF, 目标变成要证SC⊥AE，SC与AE是两异面直线，那么需考虑证明线面垂直,即证AE⊥含SC的平面SBC;逆向证AE⊥含SC的平面SBC,也就是证AE⊥SB,AE⊥BC；已知AE⊥SB，逆向证AE⊥BC，即证BC⊥含AE的平面SAB；逆向证BC⊥平面SAB，即证BC⊥SA,BC⊥AB；显然BC⊥SA,BC⊥AB都是已知.在逆向思考中不断排除干扰，与已知条件进行分析，逐层分析，从而得到问题解决.

二、在类比形式上培养学生弹性思维

类比是一种重要弹性思维培养方法，根据问题在某一方面的某种特定的性质判断它们推导出在其他方面也存在着相同或者相似性质.这种类比形式往往能够在横向上提高学生数学核心素养，强化培养学生的弹性思维宽度.

例如：已知数列{an}、{bn}是两个等比数列，那么

(1)数列cn=an·bn是否仍是一个等比数列呢？先特殊举例分析，再进行证明.

(2)教师能类比提出问题.

①数列{an+bn}是否是等比数列？数列{an-bn}是否是等比数列？

④数列{|an|}是否是等比数列？数列{can}是否是等比数列？(其中c为常数)

⑤在数列{an}中将下标成等差数列的项依次取出来组成一个新数列，这个新数列是否是等比数列？

又例如在讲三角函数的单调性时，我们可以通过一组简单的变式使学生加深对这个性质的理解：

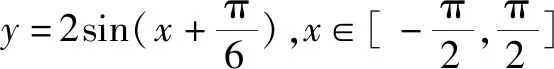
三、在发散形式上培养学生弹性思维

发散形式如同辐射出发，以一种不断扩散形式出发思考，在某一个数学问题上，一题多解很适合运用这种培养思维方式，教师以这个问题为中心，从各个不同的知识点，不同形式的思考方式展开思考的方向，不断发散，不满足只找一个正确的答案.从发散形式上分散性上提高学生数学核心素养，强化培养学生弹性思维厚度.

解法一由正弦定理

sinBcosC+sinCcosB=2sinB，

化简得a=2b，

解法三由三角形射影定理，知bcosC+ccosB=a，

故填2.

四、在矛盾形式上培养学生弹性思维

矛盾不是数学定理概念本身、也不是题目已知条件，它是一种思维方式不同产生的，学生在矛盾中发现数学的本质属性和数学知识的逻辑关系.教师可以利用这些矛盾点能让学生准确把握关键，能激活学生的思路;从而融会贯通，打通学生的“任督二脉”.在矛盾形式上聚焦性提高学生数学核心素养，强化培养学生弹性思维高度.

例如：设f(x)为R上的奇函数，且满足f(x+2)=-f(x)，若f(2)=3，求f(6)的值.

方向1：∵f(x+2)=-f(x)，

∴f(x+2)+f(x)=0 ①，

∴f(x+4)+f(x+2)=0 ②.

②-①得：

∴(x+4)=f(x),∴f(x)的周期T=4，

∴f(6)=f(6-4)=f(2)=3.

方向2：同上可得周期T=4，

∵f(x)为R上的奇函数，

∴f(6)=f(6-8)=f(-2)=-f(2)=-3.

同一个问题，不同方向，等到不同结果，这个矛盾体通过学生的检验，不断深化函数奇偶性与周期的知识，锻炼辩证思维.弹性思维得到发展.