解三角形中涉及角平分线题型的解题策略

李 宁 唐盛彪

(海南省海口市海南中学 571158)

解三角形题目中时有角平分线条件出现，如2015年全国二卷文科理科第17题、2018年江苏高考第13题. 下面结合具体题目总结这类题型的常见解题策略.

一、两个常用结论(等面积法)

遇见角平分线条件来求线段长度，常常需要用到等面积法. 下面用等面积法证明两个结论.

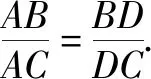
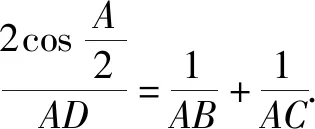
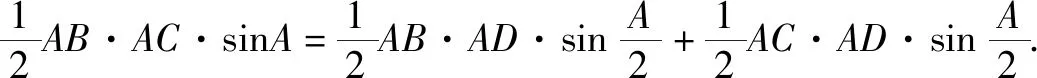
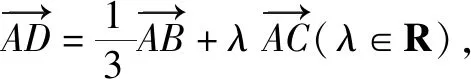
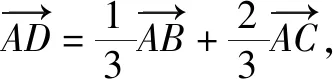
例2 在△ABC中，角A,B,C所对的边分别为a,b,c，∠ABC=120°，∠ABC的平分线交AC于点D，且BD=1，则4a+c的最小值为____.

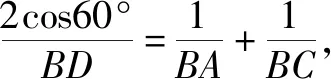
评注结论1是角平分线的重要性质，解角平分线题时常常用到. 结论2沟通了角平分线AD和边AB,AC之间的长度关系，不需要记忆，需要时用等面积法简单推导即可得到.

二、利用向量平方来算长度

例3 已知△ABC中，∠BAC=120°,AB=2,AC=1，AD是∠BAC的角平分线，交BC于D，则AD的长度为____.

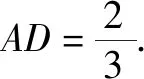
三、利用方程思想来算长度

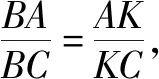
设AK=t，则BA=2t.

由于cos∠ABK=cos∠CBK，在△ABK和△CBK，分别应用余弦定理，有

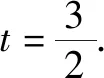
评注同一个目标用两种算法算两次，是构建方程的重要途径. 本题除了利用cos∠ABK=cos∠CBK之外，还可以利用cos∠BCK=cos∠BCA或者cos∠AKB+cos∠CKB=0来构建关于t的方程.

四、利用二倍角公式来算角的三角函数值

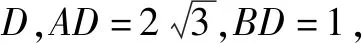
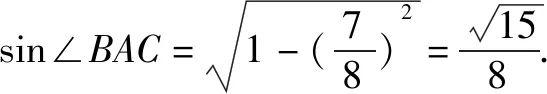
故cosC=cos(60°-∠BAC)

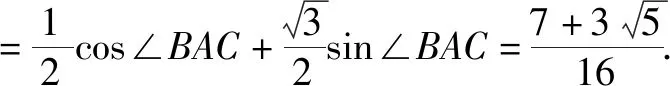
评注由于∠BAC=2∠BAD，△BAC和△BAD中，先在已知条件多的三角形中进行边角计算，再结合二倍角公式过度到另一个三角形中进行边角计算.

相关练习

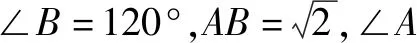
2. 在斜△ABC中，角A,B,C所对的边分别为a,b,c，已知asinA+bsinB-csinC= 4bsinBcosC，若CD是角C的角平分线，且CD=b，则cosC=____.

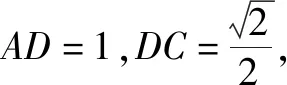
参考答案