基于近场动力学的天线罩复合材料侵彻损伤研究

赵天佑，韩如冰，査倩雯，王 敏，纪 松

(上海无线电设备研究所，上海 201109)

0 引言

导弹在飞行过程中，常常会受到飞鸟、漂浮垃圾等小型飞行物的撞击，这给弹体及天线罩的结构安全带来了一定的威胁。传统的陶瓷材料导弹天线罩罩体由于脆性高、重量大等缺点，越来越不能满足当前日益严苛的工作环境要求。复合材料由于比强度和比刚度高、设计性良好等优点，逐渐成为新型罩体材料的良好选择[1]。但复合材料各向异性的特点导致其损伤形式复杂，传统有限元方法模拟困难，在一定程度上制约了复合材料的发展和应用。2000年SILLING[2-3]提出了一种新的无网格方法——近场动力学(Peridynamics，PD)方法，该方法的本构方程简单且更贴近物理实际，能较好地模拟复合材料的损伤形式及过程。本文采用该方法分析了复合材料罩体等效结构在高速小型飞行物冲击下的渐进损伤形式，以及飞行物贯穿结构后的剩余速度情况。

1 复合材料PD理论

1.1 PD冲击模型

近场动力学作为一种新兴的非局部无网格理论，区别于传统经典理论的连续性假设，重塑了运动学方程，用空间积分方程代替微分方程来描述物质的力学行为，避免了传统方法在解决不连续问题时的奇异性。其满足一般力学定律的运动方程为

式中:ρ(x)为物质点x的密度；(x，t)为物质点x在t时刻的加速度矢量；Hx为近场域；Vx'代表物质点x'的体积；f(u(x'，t)-u(x，t)，x'-x)为近场力矢量函数，该函数与两物质点之间的初始相对位置x'-x及相对位移矢量u(x'，t)-u(x，t)相关；b(x，t)为体积力。

SILLING[4]在随后的研究中给出了基于PD理论的刚性冲击模型，本文基于此模型模拟了近场动力学中刚性飞行物与靶体间的接触过程。分析时将飞行物视为不可变形的刚体，由于冲击作用时间一般十分短暂，因此可以将冲击过程离散为准静态压缩过程。飞行物以初始速度v0运动，直到与靶体接触，此时靶体处于静止状态，每个物质点接受的点力的合力为零，如图1(a)所示。飞行物继续运动至侵入靶体，此时靶体内有物质点进入飞行物，如图1(b)所示。为了避免两者相互渗透，需要对进入飞行物的物质点进行修正，修正后的物质点被挤压到新的位置，如图1(c)所示。

图1 飞行物冲击接触的整体过程

靶体物质点修正方法如图2所示。其中U为物质点受到飞行物挤压而产生的位移；Ux和Uy分别为位移U在水平和垂直方向上的分量；θ为物质点位移方向与水平方向的夹角。

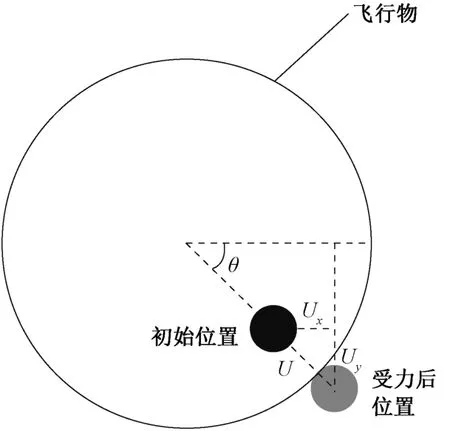
图2 物质点位移修正示意图

飞行物与靶体接触过程中，原始物质点之间的平衡状态被破坏。这反过来导致物质点的速度改变，物质点以新的速度产生新的位移。在整个过程中，飞行物将受到物质点的反作用力，从而使得飞行物的速度也发生改变并带入下一步进行迭代计算。

冲击过程中，第i步飞行物速度的迭代公式为

第i步飞行物新的位置矢量的迭代公式为

飞行物到达如图1(b)所示的新位置后，需要对进入飞行物的物质点的位置进行修正，修正后板内的物质点的新位置的计算公式为

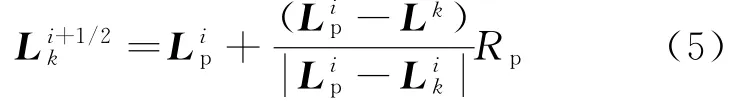
靶体内的物质点受到飞行物挤压而产生的位移的计算公式为

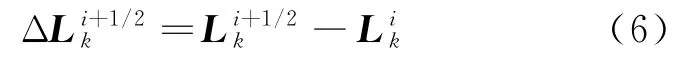
靶体内的物质点受到飞行物挤压而产生的加速度计算公式为

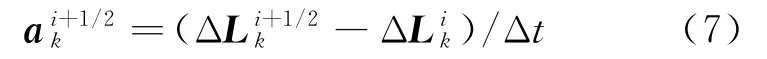
结合式(6)和式(7)，飞行物受到的反作用力可表示为

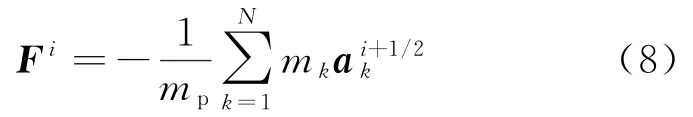
式中:mk为物质点k的质量；N表示近场域内的物质点的个数。

靶体内物质点j由于对点力平衡被破坏而产生的加速度可表示为

式中:f(·)表示物质点k、j之间的对点力函数；Vx为物质点的体积。

综上所述，可以得到靶体内任意未直接受到飞行物挤压的物质点的速度和位移矢量迭代公式为

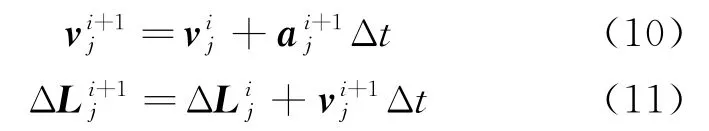
物质点的位置矢量迭代公式为

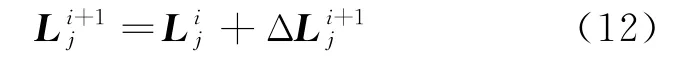
上述为冲击过程中的一次迭代过程，当一次迭代完成后即进入下一次迭代，直至整个冲击碰撞结束[5]。

1.2 损伤判据

近场动力学中假设某一物质点与特定半径区域中的任一物质点之间存在相互作用，这种相互作用通过“键”来表述，而材料的损伤是通过“键”的伸长和压缩率来定义的。当“键”的伸长率s达到临界值s0，即s＞s0时，“键”将发生断裂，并且这个过程是不可逆的。一般认为，当有“键”开始断裂时，微裂纹就开始萌生，当一系列“键”断裂后，由这些断裂的“键”所形成的不连续的空间即为宏观的微裂纹，如图3所示[6]。图中黑色圆点表示物质点，物质点之间的连接折线表示“键”，沿折线延展方向的光滑曲线即为宏观裂纹。

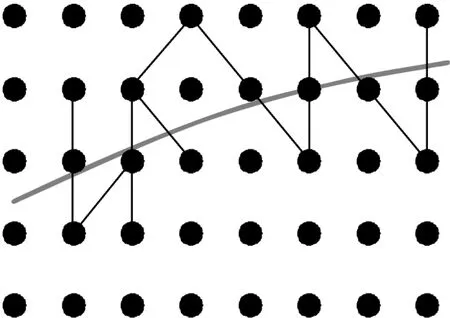
图3 键的断裂形成的损伤区域

对于复合材料而言，键的定义如图4所示。

图4 复合材料相关的PD键示意图

同一层之间沿着纤维方向的两物质点之间的“键”为纤维键，非纤维方向的为基体键；相邻两层之间垂直方向的两物质点之间的“键”为层间键，非垂直方向的为剪切键。

纤维键的临界伸长率的计算公式为[7]

式中:sft为纤维键拉伸临界伸长率；sfc为纤维键压缩临界伸长率；XT为纤维拉伸强度；XC为纤维压缩强度；E11为纤维方向弹性模量。

基体键的临界伸长率的计算公式为

式中:smt为基体拉伸临界伸长率；smc为基体压缩临界伸长率；YT为基体拉伸强度；YC为基体压缩强度；E22为基体方向弹性模量。

层间键的临界伸长率通常用sN表示[3]。破坏第n层物质点x和第(n+1)层物质点x'之间的层间键，所需要的能量与材料的Ⅰ型张开型断裂的临界能量释放率GΙ相等，表达式为

式中:d代表复合材料单层的厚度；cN为层间键常数；代表物质点x'的体积；Em为基体材料的弹性模量。可以得到层间键的临界伸长率的表达式

由复合材料键的定义可知，位于第n层的材料点x近场域内的剪切键数目多于层间键数目。并且剪切键的破坏宏观上表现为Ⅱ型滑移型断裂模式，其临界能量释放率GΙΙ表达式为

式中:H为近场域；cS为剪切键常数；φC为剪切键的临界参数，亦称为临界剪切角；V为物质点的体积；Gm为基体材料的剪切模量；δ为近场域半径。将式(17)积分区域进行分解可以得到

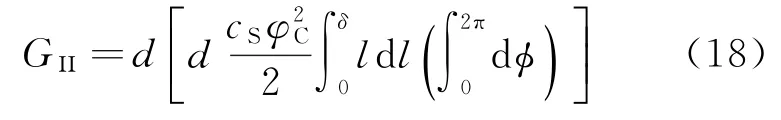
式中:l为两物质点之间的距离；ϕ为两物质点连线与水平面的夹角。

由积分结果可以得到

Ⅱ型断裂模式的临界能量释放率GΙΙ往往取决于环氧树脂的后固化温度，因此通常认为GΙΙ数值上等于3GΙ/4，此时φC=sN。

2 罩体等效结构冲击模拟

根据理论分析，基于FORTRAN语言和Visual Studio平台，编写了复合材料的近场动力学冲击计算程序。采用该程序对罩体在高速飞行物冲击作用下的渐进损伤模式及裂纹扩展过程进行了模拟，并且考虑了飞行物形状对复合材料损伤形式的影响。

2.1 渐进损伤过程分析

为了探究高速飞行物冲击作用下复合材料的渐进损伤模式，采用前文所述的简化层合板冲击模型，对1 000 m/s速度下的高速球形刚性飞行物穿透层合板罩体材料的情况进行了模拟仿真。飞行物及层合板几何形状示意图如图5所示。

图5 飞行物及板几何形状示意图

图5中，受冲击板的几何尺寸为300 mm×300 mm×20 mm，边界条件为四面固定支撑。球形飞行物半径r=8 mm，密度7 850 kg/m3。层合板单层材料为碳纤维复合材料CCF300/10128 H，材料的基本性能参数如表1所示。

表1 CCF300/10128H材料基本性能参数

层合板采用的铺层方式为[45/0/-45/0/90]2s，单层厚度为1 mm，共20层。PD模型中层合板长度和宽度方向均设置300个物质点，粒子间距Δx=1 mm，物质点体积ΔV=1.0×10-9m3，近场半径δ=3.015Δx，取时间步进Δt=2×10-8s，满足稳定性要求。

模拟结果显示，高速飞行物冲击作用下复合材料层合板的损伤形式以基体损伤为主，其损伤过程如图6所示。

图6 冲击渐进损伤过程

由图6可知，复合材料层合板在受到高速飞行物冲击时，会发生侵彻和穿透现象。整体而言，层合板表面在冲击中心位置的损伤程度最大，随着冲击时间的推移，损伤由中心位置向周边逐渐扩展。对比不同时刻的损伤结果可以看出:冲击发生的早期，层合板损伤裂纹主要沿45°方向扩展；随着冲击作用的累加，逐步出现-45°方向扩展的裂纹，但其扩展程度远小于45°的损伤程度。总体而言，随着冲击时间的增加，层合板损伤的裂纹长度逐渐增加直至稳定，接着损伤逐渐向冲击点位置集中，损伤扩展不再具有明显单一的方向性，而是沿着多方向多分叉扩展。

2.2 飞行物形状的影响

为了研究飞行物的形状对层合板结构损伤及飞行物剩余速度的影响，选取球状、柱状和圆头柱状分别进行模拟计算。三种飞行物的外形如图7所示，尺寸分别为:球状半径r1=8 mm；柱状半径r2=8 mm，高h2=8 mm；圆头柱状半球及柱体半径r3=8 mm，柱体高度h3=8 mm。冲击速度v=1 000 mm/s，飞行物材料参数、层合板的几何尺寸和材料参数以及层合板的PD参数都与2.1节相同。

图7 不同形状的飞行物示意图

三种形状的飞行物作用下的层合板上表面的渐进损伤过程如图8所示。

图8 不同形状飞行物对应的层合板基体损伤情况

从图8可以看出，球状飞行物冲击下，层合板的初始损伤区域为圆形，且冲击点中心位置的损伤最大。随着时间的推进，层合板的损伤逐渐向45°方向扩展，当损伤达到一定程度后，损伤区域45°方向的两端逐渐形成两条细长的平行但不对称的裂纹。在4×10-5s左右时，裂纹扩展长度达到最大值，此后两端的裂纹不再进一步扩展。而中部损伤区域则会进一步变大，最终损伤区域呈现为不规则的“梭”形，并在板中心点位置逐渐形成圆形破口。

柱状飞行物冲击下，层合板的初始损伤区域为圆环形。随后圆环形损伤区域的面积略微增大，当损伤达到一定程度后，大约在2×10-5s时，损伤区域45°方向的两端逐渐形成两条细长的平行对称的裂纹。在4×10-5s左右，45°方向的裂纹扩展长度达到最大值。随后损伤区域-45°方向的两端形成两条较短的平行对称的裂纹。在1×10-4s裂纹停止扩展，损伤区域则会进一步变大，损伤区域的最终形式仍为近似圆环形，圆环中心位置形成破口。

圆头柱状飞行物冲击下，层合板的损伤形式与球状飞行物冲击下的类似，初始损伤区域也为圆形，中心位置的损伤程度最大，损伤区域45°方向形成两条很短的平行对称的裂纹，损伤区域的最终形式为较为规整的“梭”形，板中心位置破口很小。

对比不同形状飞行物冲击下层合板的损伤结果可以发现:球状飞行物冲击下，层合板的整体损伤区域的面积及损伤的程度最大，圆头柱状其次，柱状最小；柱状飞行物冲击下，层合板的裂纹扩展的长度最大，圆头柱状最小；柱状飞行物冲击下，层合板的中心破口的面积最大，球状次之，圆头柱状最小。

图9给出了球状、圆头柱状和柱状飞行物冲击层合板的速度衰减情况。飞行物进入层合板后，柱状飞行物的速度衰减速率最大，贯穿层合板所用的时间最短；球状飞行物的速度衰减速率最小，贯穿层合板所用的时间最长；圆头柱状飞行物的速度衰减速率和贯穿时间介于上述两种形状的飞行物之间。飞行物贯穿层合板后，球状飞行物的剩余速度最大，圆头柱状次之，柱状飞行物剩余速度最小。可以看出:相同初速度下，柱状飞行物能够最快地贯穿层合板，但是其贯穿层合板需要消耗的能量最大；球状飞行物贯穿层合板的速度最慢，但是消耗的能量最低；圆头柱状介于两者之间。出现上述结果的原因主要与飞行物几何形状的圆润度有关，一般来说飞行物越尖锐，其贯穿层合板的速度则越快，而飞行物的圆度越大，其贯穿层合板所需的能量则越低。

图9 三种飞行物的速度衰减示意图

3 结论

本文采用近场动力学方法研究了高速飞行物冲击作用下，复合材料层合罩体结构随时间的渐进损伤变化过程。分析了其损伤变化形式及规律，并且考虑了飞行的几何形状和对结构的损伤情况以及飞行物剩余速度情况的影响。研究表明:在小质量高速飞行物冲击作用下，罩体复合材料层合板结构会发生侵彻和穿透现象，结构的损伤形式以基体损伤为主，损伤形式随时间渐进变化；不同形状的飞行物冲击下，层合板上下表面损伤区域的形状及大小存在一定差异，总体而言飞行物越尖锐，其贯穿层合板的速度则越快，而飞行物的圆度越大，其贯穿结构所需的能量则越低。