巷道掘进围岩纵向变形分析与支护技术
谷拴成,王 彬,孙 魏
(西安科技大学 建筑与土木工程学院,陕西 西安 710054)
巷道在开挖后,原岩应力将会发生改变,应力将会重新分布,在开挖面不断向前推进的过程中,由于空间效应的存在,巷道前期围岩变形比较缓慢,巷道能够在一定时间内保持自稳。随着开挖面向前循环推进,距离工作面附近一定范围内,围岩应力缓慢释放,围岩处于弹性变形阶段,随着开挖面继续推进,围岩变形进入弹塑性阶段[1-2]。在开挖面空间效应作用下,围岩应力重分布不能一次性完成,在距开挖面一定范围内的巷道围岩纵向变形将随着工作面的不断推进而分次释放[3],因此深入研究开挖面的空间效应影响,对巷道前期及时支护确保巷道稳定有深远意义。
孙均[4-5]等对软弱破碎围岩硐室施工特性进行力学模拟,并分析了隧道开挖面的空间效应。朱合华[6]等人提出“广义虚拟支撑力法”,将三维空间转为二维平面问题,进行二维黏弹塑性分析。高峰[7]等研究施工过程中支撑荷载,用有限元法讨论释放荷载和支撑荷载的关系,并结合三维模型计算结果确定位移释放率。崔岚[8]等人对于静水压力下的圆形隧道,提出弹-脆-塑性围岩下虚拟支护力的数值方法,研究了临界塑性软化系数、剪胀系数、初始应力对开挖面空间效应的影响。张晓飞[9]等人基于开挖面空间效应理论,对圆形巷道开挖面空间效应进行了分析,研究了煤巷锚杆支护结构的支护特性。曾开华[10]等人基于隧道开挖面的空间效应提出了考虑开挖面空间效应的隧道支护设计新方法。赵旭峰[11]等从围岩黏弹性的角度分析,建立三维模型,结果表明开挖面的空间效应影响围岩变形,掘进工作面对其附近围岩有支撑作用。侯公羽[12-13]建立围岩弹塑性变形二次释放的力学简化模型,研究了围岩与支护结构相互作用。M Panet、Hoek[14-15]等人根据理论分析和大量的隧道现场监测,均取得了一定的研究成果,得到了不同的位移释放系数表达式,对开挖面的空间效应研究有重大意义。
综上前人对于开挖面的空间效应已经做了大量的研究,但没有针对巷道在掘进过程中,距开挖面一定距离处巷道围岩的塑性区半径、纵向变形以及应力变化与开挖距离的关系进行深入研究。通过建立巷道纵向位移与开挖面虚拟支护力关系的数学模型,研究围岩的纵向位移与应力变化,根据巷道围岩位移、应力释放的变化规律,能够更好地对进行巷道支护设计。
1 开挖面空间效应
巷道在未开挖时岩体处于受力平衡状态,巷道开挖后,破坏了初始状态的受力平衡状态,引起应力、变形重新分布。巷道围岩的应力-应变是非线性的,当巷道切向应力达到或者超过围岩的屈服强度时,围岩进入塑性变形状态,产生塑性区[16]。但围岩并没有立即产生破坏,由于巷道开挖面的“端面效应”存在,巷道围岩周围存在虚拟支护力,使围岩的变形和应力不能一次全部释放,距离开挖面一定范围内巷道能够保持一定时间的自稳。巷道围岩变形过程如图1。
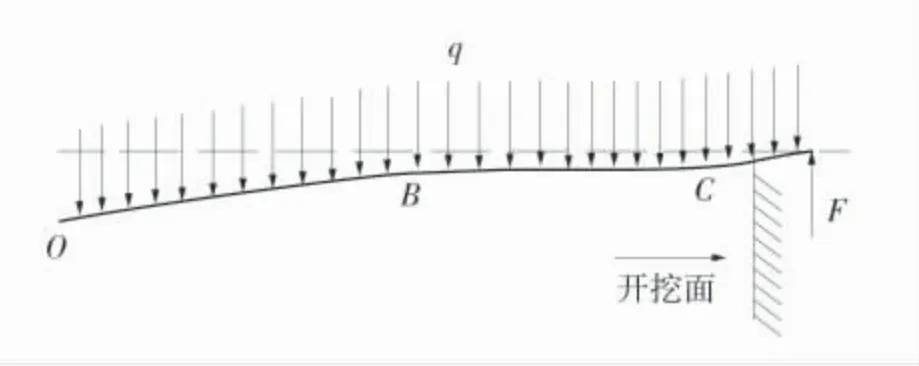
图1 巷道围岩变形过程Fig.1 Surrounding rock deformation process of roadway
巷道开挖后工作面前方的岩体会对附件围岩起到支撑作用,围岩变形的发展受到一定程度制约。在开挖面前方一定距离围岩就已经开始变形。当某一点B 距离开挖面C 很近时,B 点处围岩必然受到开挖面支撑力F 的影响,在力F 作用下,刚开挖的巷道围岩能够保持一定时间的受力平衡状态,点B越接近开挖面C,则受到的虚拟支撑力F 就越大,围岩变形就越小[17]。
在原岩应力p0以及巷道周边虚拟支护力pi作用下,径向位移围岩释放系数可采用Hoek 拟合方程计算[18-19]:
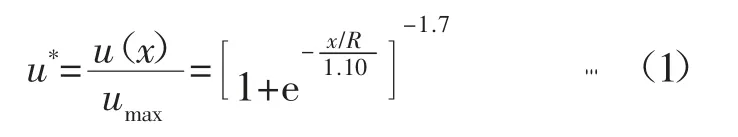
式中:x 为到开挖面的距离;R 为巷道的半径;u(x)为任一点处围岩的位移;umax为围岩的最大位移值;u*为径向位移释放系数。
开挖面空间效应如图2。点A 代表在开挖面前方已经开始受到开挖面“端面效应”影响的位置,巷道围岩位移释放系数u*接近于0,点B 代表为开始支护的位置,点C 代表在无支护条件下,围岩位移释放达到最大,不再受开挖面空间效应影响的位置,巷道围岩位移释放系数u*接近于1。开挖面位置坐标轴x/R 取值范围应以u(x)/umax的比值满足工程和设计允许的误差为原则。取开挖面前4R 和开挖面后6R,误差分别为0.197 7%和 0.722 9%,满足要求。
2 巷道开挖围岩力学分析
2.1 未支护状态下力学模型
基本假设:①巷道为圆形;②将围岩视为均匀、连续、各向同性的多孔介质,无蠕变,围岩性质为理想弹塑性体,符合Mohr-Coulomb 强度准则,并处于平面应变状态。
巷道产生变形的原因是巷道开挖破坏原有的应力平衡状态,围岩应力重新分布。巷道开挖后,围岩的实际应力场[σ]为初始应力场[σ0]与开挖释放应力场[σ′]的叠加,以公式表示为:
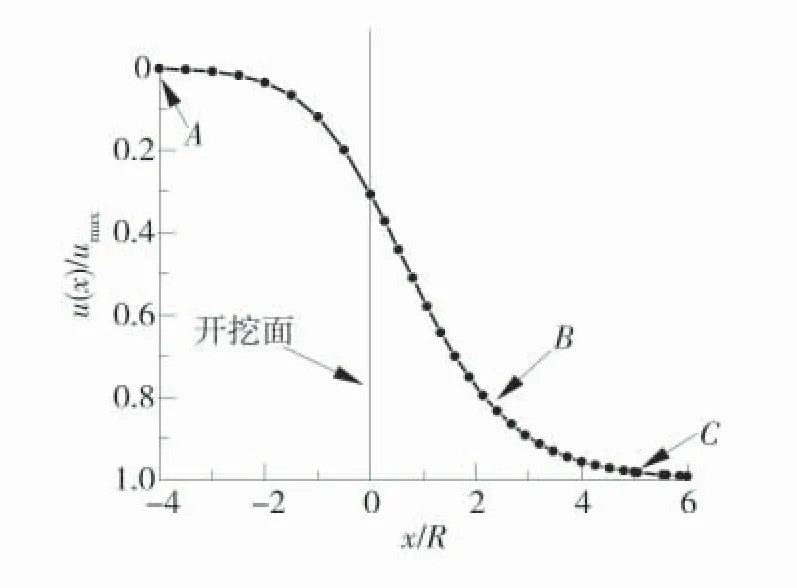
图2 开挖面空间效应Fig.2 Spatial effect of excavation surface

将开挖面的空间效应影响的某一截面转化为施加在该截面的虚拟支撑力,建立的无支护条件的力学模型如图3。
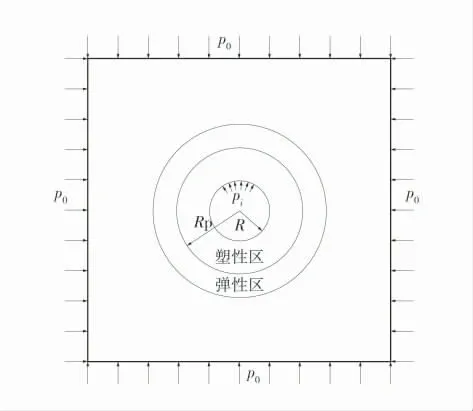
图3 基于开挖面空间效应未支护下的力学模型Fig.3 Mechanical model based on spatial effect of excavation surface without support
p0为原岩应力;pi为开挖面空间效应影响下的虚拟支撑力。
巷道在无任何支护条件下,在原岩应力作用下只发生径向弹性位移,由弹性解位移公式得:

式中:ue为径向弹性位移;R 为巷道半径;μ 为围岩泊松比;E 为围岩弹性模量。
在虚拟支撑力(支护反力)pi作用在巷道内周边,此时巷道径向弹性位移为:
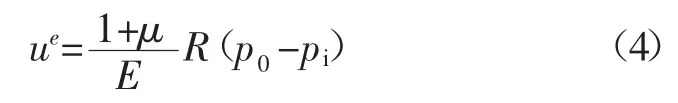
将式(1)、式(3)、式(4)联立得:
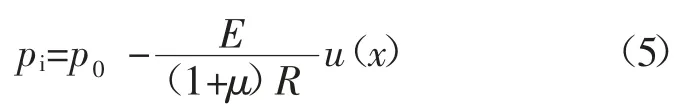
围岩在无支护条件下,在虚拟支撑力pi作用下发生径向弹塑性位移,基于Mohr-Coulomb 屈服准则的弹塑性位移计算:
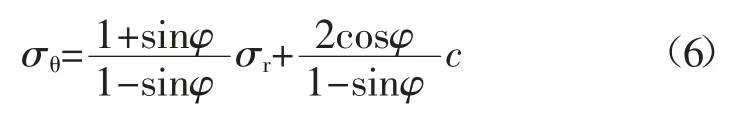
开挖状态以虚拟支撑力表示的塑性区应力为:
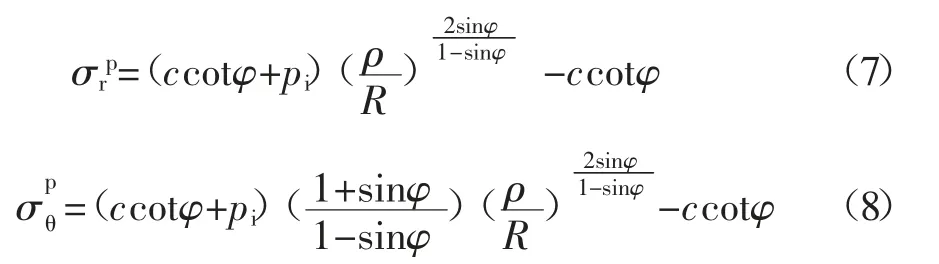
式中:c 为围岩黏聚力;φ 为围岩内摩擦角;ρ 为距离巷道中心距离;σθ为切向应力;σr为径向应力;分别为塑性区的径向应力和切向应力。
塑性区半径Rp为:
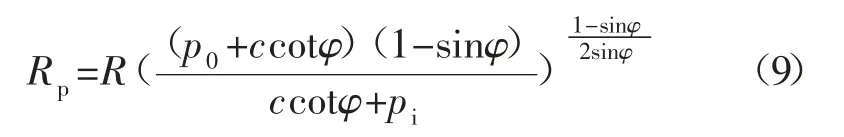
假设塑性区体积不可压缩,巷道围岩弹塑性位移计算公式:
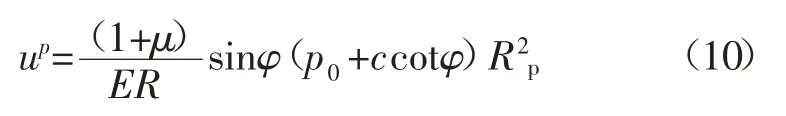
联立式(1)、式(9)、式(10)得:
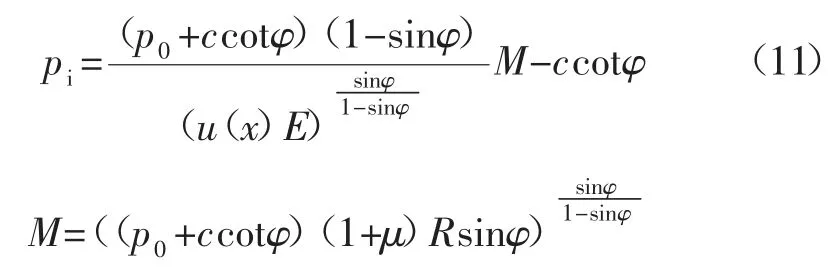
式中:c 为围岩黏聚力;φ 为围岩内摩擦角;μ 为围岩泊松比;E 为围岩弹性模量;pi为虚拟支护力;p0为原岩应力。
依据开挖面空间效应和Mohr-Coulomb 强度准则,推导出巷道开挖面虚拟支护力pi与开挖面距离x 的数学关系表达式,变化规律如图4。围岩应力释放与虚拟支护力成反比,在开挖面前方4R 处围岩未产生变形,虚拟支护力pi=p0;随着开挖面不断向前推进,围岩变形逐渐增大,开挖面对后方围岩的虚拟支护力逐渐减弱。
将式(11)代入式(9),塑性区半径与开挖距离的关系为:
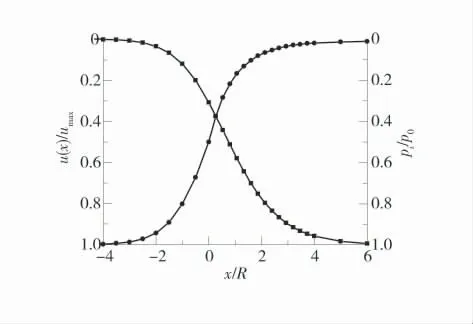
图4 巷道开挖围岩位移与开挖面虚拟支护力的变化规律Fig.4 Variation law of surrounding rock displacement and virtual support force of excavation surface of roadway excavation
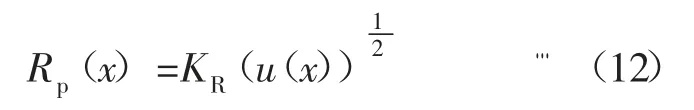
其中:
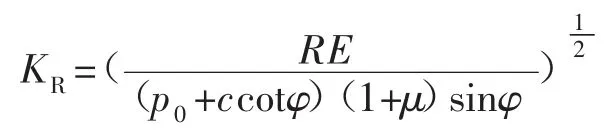
巷道开挖在无支护条件下,顶板荷载p(x)与开挖距离的关系为:
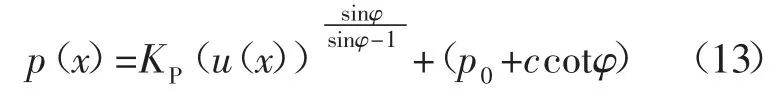
其中:
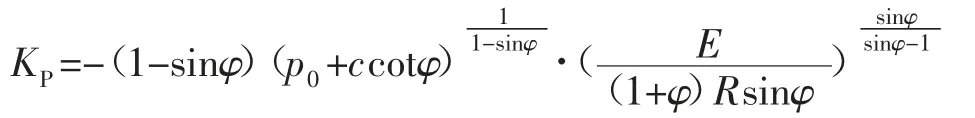
在无支护的情况下,在开挖面空间效应的作用下,围岩应力缓慢释放,应力的释放导致围岩产生变形,围岩应力释放越小则产生的变形越小,随着远离开挖面,开挖面的虚拟支护作用减弱,巷道围岩应力释放逐渐增大,围岩变形越来越大。围岩应力与位移变化规律如图5。
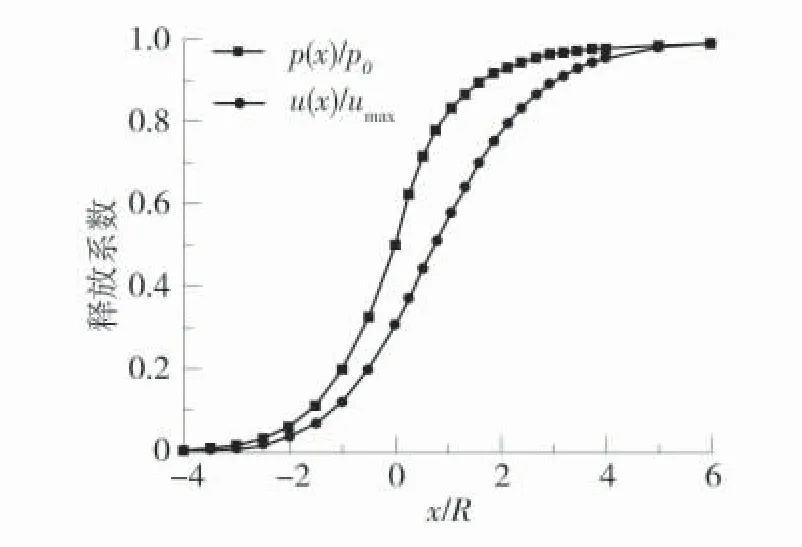
图5 围岩位移释放、应力释放与开挖面距离的变化规律Fig.5 Variation law of displacement release and stress release of surrounding rock and distance of excavation surface
2.2 支护状态下力学模型
基于开挖面空间效应支护下力学模型如图6。
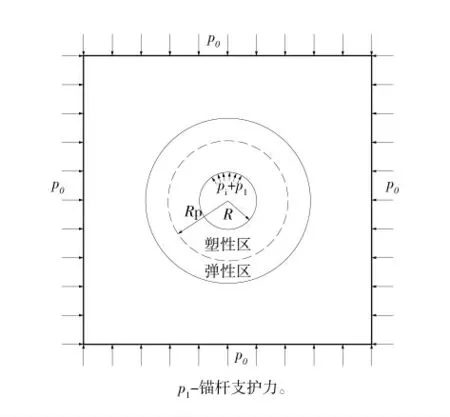
图6 基于开挖面空间效应支护下的力学模型Fig.6 Mechanical model based on spatial effect of excavation surface support
在虚拟支撑力和锚杆支护力(支护反力)p1作用在巷道内周边,此时巷道径向弹性位移U 为:
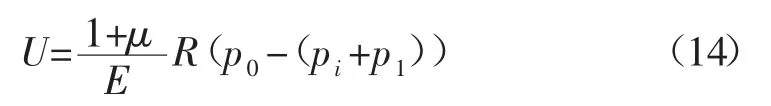
在无支护条件下,巷道虚拟支护力为:
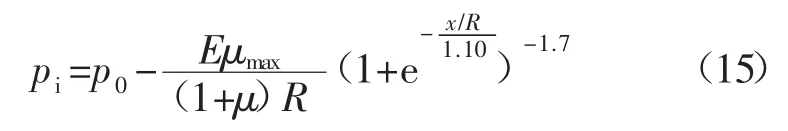
联立式(14)、式(15)得:
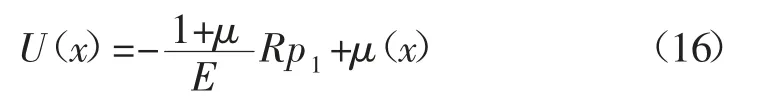
开挖状态在虚拟支撑力pi和支护力p1作用下,基于Mohr-Coulomb 屈服准则塑性区应力为:
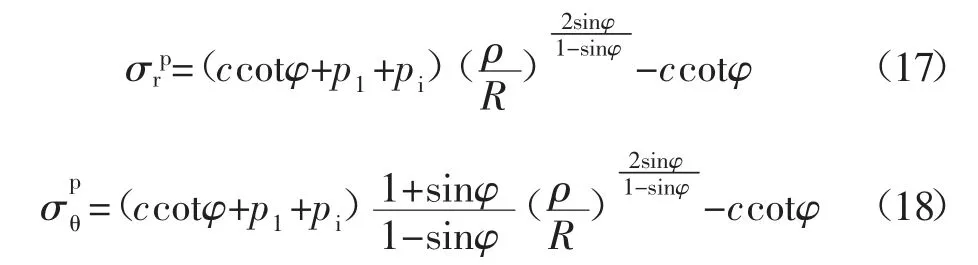
塑性区半径为:
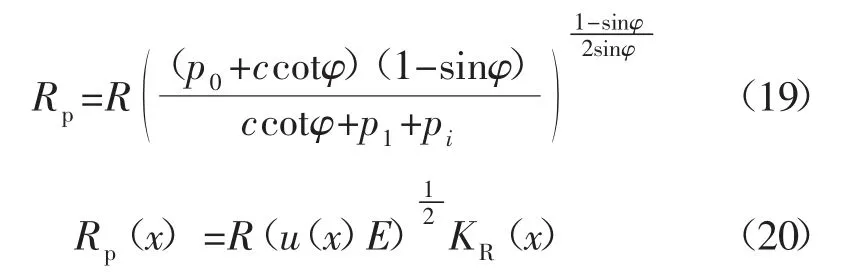
其中:
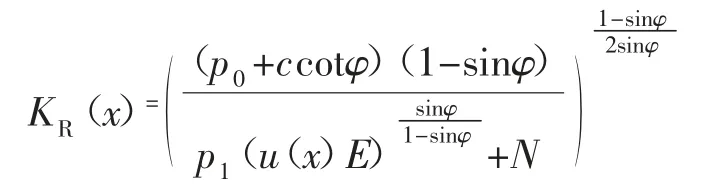
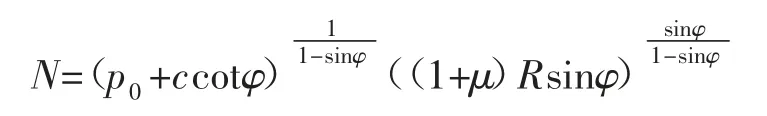
假设塑性区体积不可压缩,巷道围岩弹塑性位移计算公式:
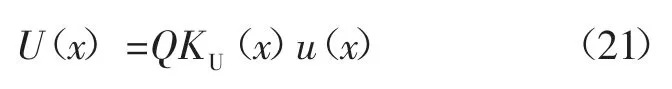
其中:
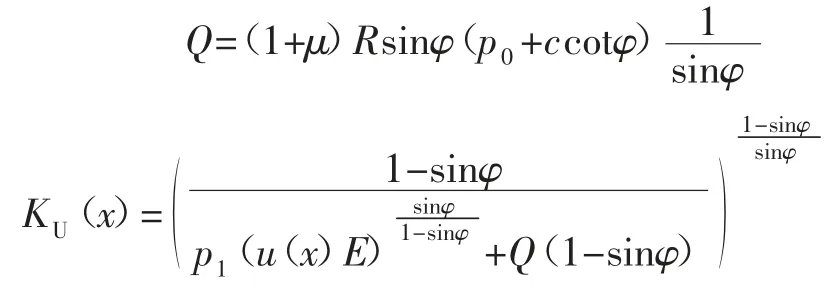
3 算例分析
柠条塔N1212掘进巷埋深 200 m,原岩应力p0=5.0 MPa,巷道半径 R=3.75 m,岩体弹性模量 E=2 000 MPa,泊松比为 0.3,围岩黏聚力 c 为 0.6 MPa,围岩内摩擦角φ 为30°。同时利用数值模拟软件FLAC3D建立模型进行分析,建立巷道模型尺寸100 m×60 m×200 m,巷道开挖半径 3.75 m。
对自y=0 正向开挖模型35 m,并设置不平衡比率6×10-4,为研究巷道开挖后拱顶应力变化情况,对开挖求解的模型进行切片处理,求得的模型稳定后围岩应力切片云图如图7。
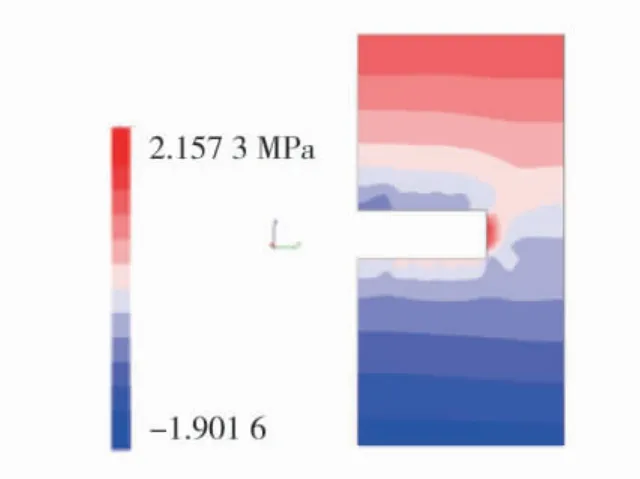
图7 模型应力切片云图Fig.7 Stress section cloud diagram of the model
根据模型应力切片云图,在开挖面处,巷道围岩应力释放约为 2.175 MPa,根据式(13)理论计算的结果,在开挖面处应力释放为1.82 MPa,两计算相差8.6%左右。通过理论计算巷道最终沉降量为20 mm。在掌子面附近,其沉降量为6.2 mm,为最终沉降量的31%,与Pane 等提出的掘进工作面未开挖前位移量为最终位移量30%~50%大致相近[20]。在掘进工作面前方,位移量均小于掌子面处的沉降量,这与巷道围岩开挖面的空间效应有关,开挖面对围岩前方有虚拟支撑作用。
根据式(12)和式(20)分别计算在无支护条件下和支护条件下巷道围岩的塑性区半径,在无支护条件下,在距离开挖面0~0.5R 处由于虚拟支护力比较大,围岩相对塑性区半径Rp/R 小于1,则可认为巷道围岩未出现塑性区。在支护条件下,在距离开挖面0~1.5R处,围岩相对塑性区半径Rp/R 小于1。通过对比未支护和支护条件下相对塑性区的变化,支护条件下在距离开挖面3R~6R 范围内,塑性区得到有效控制。相对塑性区半径R 与开挖距离的变化规律如图8。
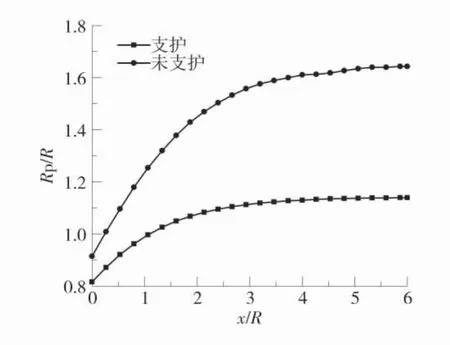
图8 相对塑性区半径R 与开挖距离的变化规律Fig.8 Variation law of relative plastic zone radius Rp/R and excavation distance
围岩位移与开挖面距离的变化规律如图9,与无支护条件下相比,支护条件下巷道围岩纵向位移受到一定约束,施加一定的约束,在每一截面处进行有效支护,巷道围岩位移释放可减小10%~15%。紧跟巷道开挖面进行支护设计,利用围岩自承能力,充分考虑围岩开挖过程中的位移和应力释放,能够有效的对巷道进行支护。
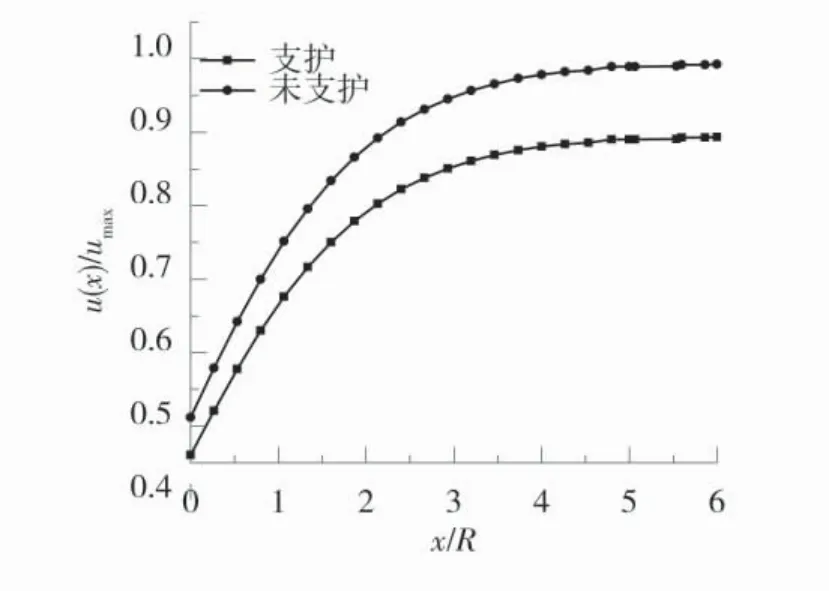
图9 围岩位移与开挖面距离的变化规律Fig.9 Variation law of displacement of surrounding rock and distance of excavation surface
4 结 论
1)基于开挖面空间效应,依据Hoek 拟合的位移释放系数方程,建立描述巷道顶板径向位移与力学模型中虚拟支护力关系的数学模型,推导出巷道在未支护条件下虚拟支护力随着开挖面距离变化的数学表达式。
2)依据Mohr-Coulomb 强度准则,对巷道开挖时围岩纵向变形进行弹塑性分析,导出空间效应下的塑性区半径、以及巷道围岩纵向变形的关系式,进而可以求得距离开挖面每一截面处的塑性区半径和围岩变形,对巷道进行及时有效的支护,保证巷道稳定。
3)通过建立的力学模型分析,结合算例分析和数值模拟,紧跟开挖面进行及时支护,可有效减缓围岩塑性区的发展,验证了本文建立力学模型的合理性,充分利用巷道空间效应,依靠围岩自承能力指导巷道的前期支护设计,有利于巷道保持稳定,对实际工程应用有重大意义。

