基于改进马尔科夫特征的图像拼接检测研究

刘进林，李欣竹，蒋晨琛

(中国人民公安大学 警务信息工程与网络安全学院，北京 100038)

0 引言

随着信息技术的发展，图像伪造成本变得越来越低，带有恶意目的的图像篡改给人类社会带来许多不利的影响。图像拼接是图像伪造中最常见的手段，图像拼接检测领域的研究日益增多，提出了各种检测图像拼接的方法。

前些年，检测图像拼接的方法主要集中在拼接图像造成的不连续性引起的全局统计性质的变化上。文献[1]提出了结合小波域的函数矩特征与Hilbert-Huang变换(HHT)进行拼接检测。文献[2]提出了结合函数矩特征与二维相位一致性的方法。利用全局统计性质变化进行检测的方法不足之处是特征维数高而且准确率不高。

近几年，已经提出了提取图像拼接区域局部变化进行图像拼接检测的方法。文献[3]提出基于可操纵金字塔变换(SPT)和局部二值模式(LBP)的图像拼接检测方法，用支持向量机(SVM)进行分类。文献[4]提出基于局部三值模式(LTP)描述图像统计特征的方法。文献[5]提出了基于多尺度局部Gabor相位量化的方法。这些方法的准确率较高但是特征维数高，算法时间复杂度高。

基于马尔科夫特征的方法[6-14]是利用图像拼接区域局部变化进行检测的，是检测性能最好的方法之一。马尔科夫特征从多年前就已经应用于图像拼接检测领域，近两年马尔科夫特征的不断优化成为发展趋势。马尔科夫特征主要在空域[10]、DCT域[6-10,13-14]、DWT域[8-9,12]、QDCT域[11]进行提取应用于拼接检测。文献[6]提出将矩特征与马尔科夫特征相结合的方法。文献[7]融合了马尔科夫和DCT特征。文献[8]提取DCT域与DWT域的马尔科夫特征。文献[9]提出了基于二维非因果马尔科夫模型的方法。文献[10]提出了基于空域和DCT域的马尔科夫特征的方法。文献[11]提出了基于四元数离散余弦变换(QDCT)域的马尔科夫特征的算法。文献[12]提出了基于分块DWT的方法。以上方法普遍存在特征维数高时间复杂度高、需要额外的降维算法对特征进行降维的问题。文献[13]提出了基于改进的马尔科夫特征，所提出的算法在离散余弦变换(DCT)域中提取系数马尔科夫特征和分块马尔科夫特征。文献[14]提出基于量化马尔科夫特征的拼接检测方法。上述方法都有较高的准确率，这可以说明马尔科夫特征的性能十分良好，同时还存在一些待研究的问题，仍有很大的发展空间。在空域、DWT域、QDCT域提取的马尔科夫特征维数都很高，DCT域的特征维数相对较低。提出维数低、性能更加良好、有更好的适用性和实用性的方法是十分必要的。

1 改进马尔科夫特征

马尔科夫特征是经典的概率特征，同时也是当前用于拼接检测中性能最好的特征之一。根据随机过程理论，马尔科夫随机过程是提取像素相关性的一种工具，而图像/系数二维矩阵中，像素/系数之间存在相关性，拼接操作改变了图像像素之间的相关性。转移概率矩阵可以用来表示马尔科夫过程。

1.1 基于马尔科夫特征的图像拼接检测

在图像拼接检测中，首先将数据集分为训练集和测试集，再提取特征，然后训练分类器，最后进行分类测试。

在DCT域提取马尔科夫特征传统方法的基本步骤如下，对于一张大小为M×N的图像：

(1)变换领域：用B(x,y)表示一个8×8的图像块中的一个空域位置的值(1≤x,y≤8)，将B(x,y)从空间域转换到DCT域：

D(u,v)=DCT(B(x,y))

(1)

其中D(u,v)是与B(x,y)对应的DCT块内的值，(u,v)(1≤u,v≤8)是DCT域的频域位置。

(2)计算差分矩阵：传统的马尔科夫特征计算块内的水平、垂直、主对角线、副对角线四个方向的差分矩阵。水平计算公式如公式(2)所示：

C→(u,v)=D(u,v)-D(u+1,v)

(2)

(3)取阈值T(T为整数)，对上述差分矩阵的值进行截值操作，对于大于T的值取为T，小于-T的值取为-T，在-T与T之间的值取其整数部分。

(4)计算转移概率矩阵：

P(s,t)=Pr(F(u,v)=s|F(u′,v′)=t)

(3)

其中P(s,t)表示不同方向的马尔科夫特征，(s,t)∈{(n1,n2)|n1,n2=-T,…,-1,0,1,…,T}，每一个方向的特征维数为(2T+1)×(2T+1)。

提取完特征后，将训练集特征输入到支持向量机(SVM)中进行训练，将测试集特征输入到训练好的分类器中进行分类测试。

1.2 改进马尔科夫特征提取

改进马尔科夫特征提取过程：

(1)分通道：分别提取彩色图像的R、G、B三通道图像。彩色图像大小为M×N×3，得到三个大小为M×N的二维矩阵，分别对每一个通道作如下操作。

(2)变换域：对矩阵进行8×8分块的离散余弦变换，将图像从空域转换到频域，得到DCT系数矩阵，取绝对值后再取整，如公式(1)所示。

(3)计算差分矩阵：对DCT系数矩阵分别计算两种(块内、块间)、两个方向(水平、垂直)的差分矩阵，得到四个差分矩阵。

(4)

(5)

(6)

(7)

其中，1≤u≤N,1≤v≤M上标表示差分矩阵的方向，下标intra表示块内运算，inter表示块间运算。

(4)取阈值T：对四个差分矩阵的所有元素值的范围约束在[-T,T]之间。

(5)计算马尔科夫特征：对块内、块间的水平、垂直差分矩阵分别计算对应的水平、垂直转移概率矩阵，得到四个块内的转移概率矩阵和四个块间的转移概率矩阵。

(8)

(9)

(10)

(11)

(6)求和：对块内、块间转移概率矩阵分别求和，即求每个通道块内、块间四个转移概率矩阵的和，得到两个转移概率矩阵，作为最终特征。当T=3时，(2T+1)×(2T+1)=49，每个颜色通道的特征维数为98。

(12)

(13)

得到马尔科夫特征，用于下一步分类。

(14)

图1表示改进马尔科夫特征提取的流程。在图中，方框中的箭头表示差分矩阵与转移概率矩阵的方向。实线表示块内运算，虚线表示块间运算。

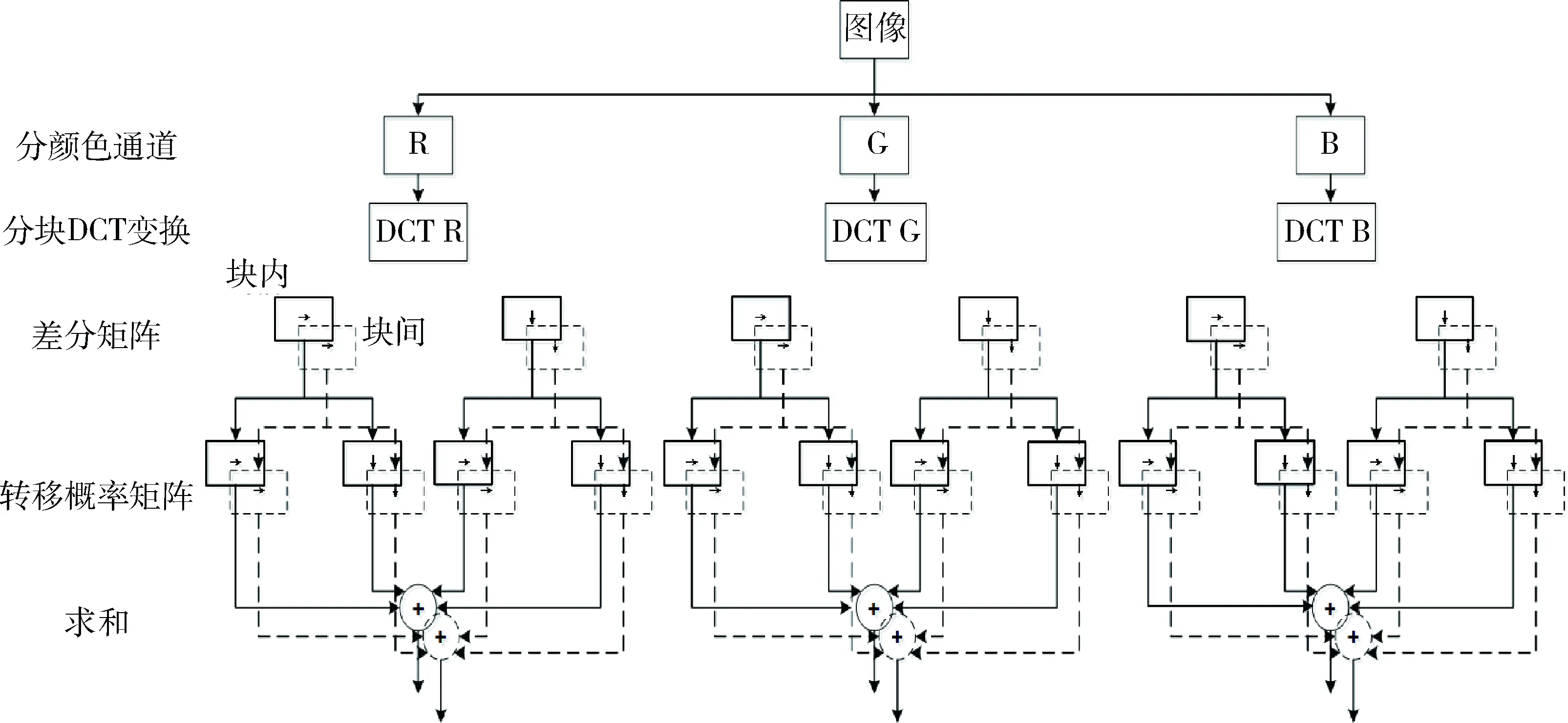
图1 改进马尔科夫特征提取方法

本文提出的特征具有以下特点：(1)彩色图像提取颜色通道图像，而不是直接转为灰度图。将彩色图像转换成灰度图像后进行检测，在一定程度上改变了原始图像的统计特征，掩盖了拼接的痕迹，降低检测效果。(2)不是直接在空域上求马尔科夫特征，而是在变换域上提取特征。与空域相比，在变换域上使用马尔科夫特征具有更好的检测性能。(3)将转移概率矩阵作用于差分矩阵而不直接作用于原图像矩阵。差分矩阵中的元素分布以某种方式围绕着零，分布集中在零上的程度反映了像素/系数之间相关性的强弱。将转移概率矩阵应用在差分矩阵上，不仅可以降低马尔科夫转移概率矩阵的维数而且可以更好地获取像素相关性，提取出更明显的痕迹，减少图像内容带来的影响。(4)计算块间的差分矩阵。不只计算块内的差分矩阵，计算块与块之间的差距，获取更全面有效的信息。(5)取阈值T。由于变换域内的差值矩阵具有较大的动态范围，特征的数量会非常大，需要取阈值控制得到特征的维数。(6)求和操作。当T=3时，不求和的特征维数为392，求和后特征维数为98。不需要额外的降维算法，用求和操作不仅可以得到更好的图像拼接特征而且可以达到降维的目的。

2 实验与结果分析

对实验所用到的数据集、分类方法和评价指标进行说明。在三个公开数据集上进行实验，并与其他方法进行对比。

2.1 数据集选择与分类

选用三个公开的数据集：哥伦比亚彩色拼接检测图库[15]、CASIA V1.0[16]与CASIA V2.0。哥伦比亚彩色数据集包括183张原始图像和180张篡改图像，图像大小从757×568到1 152×768，图像格式为TIFF格式，全部为简单的拼接图像。CASIA V1.0数据集包括800张原始图像和921张篡改图像，图像大小为374×256，图像格式为JPEG格式，均为有前处理的拼接图。CASIA V2.0数据集包括7 200张原始图像和5 123张篡改图像，图像大小从320×240到800×600，原始图像有JPEG和BMP格式，篡改图像有JPEG和TIFF格式，拼接图有前处理和后处理操作。

使用支持向量机(SVM)分类器[17]，使用网格算法寻找最优参数，用六倍交叉验证来评估SVM模型参数，即随机选择整个数据集5/6的图像作为训练集，剩余1/6作为测试集，共进行30次独立的随机实验，并取平均结果作为实验结果，以减少随机带来的影响。用三个评价指标来衡量算法的性能：查全率(Recall)，查准率(Precision)，准确率(Accuracy,ACC)。Recall=TP/(TP+FN)，表示检测正确的拼接图像数占数据集中所有拼接图像数的比例；Precision=TP/(TP+FP)，表示检测正确的拼接图像占所有检测为拼接图像的比例；ACC=(TP+TN)/(TP+FN+FP+TN)，代表数据集所有图像分类正确的图像所占比例。其中，TP表示在所有拼接图像中预测正确的拼接图像数，FN表示在所有拼接图像中错误预测成原始图像的图像数，TN表示在所有原始图像中预测正确的原始图像数，FP表示在所有原始图像中错误预测成拼接图像的图像数。

2.2 参数选择与实验

本文有一个变化参数阈值T，阈值T是在求转移概率矩阵之前对差分矩阵进行值的限制，T决定着特征的维数大小。如果T太大会产生冗余信息进而增加计算的时间复杂度；如果T太小，就会带来过多的信息损失，不能很好地捕获差分矩阵中系数的关联性，无法区分真实图像与拼接图像。本文分别采用T=2、3、4进行实验。

在拼接检测时，每一张图提取三个颜色通道的特征，如图1所示。每个特征单独训练一个SVM分类器，共三个SVM分类器。测试时，用训练好的SVM分类器对图像进行分类。在决策时，采用三选二的方式进行综合决策，即R、G、B三个通道，如果两个通道及以上判断为拼接图则认为是拼接图。

在哥伦比亚彩色数据集上的实验结果如表1所示。随着T值的增大，查全率基本没有变化，而查准率在逐步上升，当T=3时准确率达到了94.38%，每个通道的正确率都在90.69%以上。

表1 在哥伦比亚彩色数据集上的实验结果(%)

在CASIA1数据集上的实验结果如表2所示。查全率并没有随着T值的增大而有多大变化,保持在98%左右,而查准率提升了3%,当T=4时达到了最高的准确率99.19%,每个通道的正确率也都在97.75%以上。

在CASIA2数据集上的实验结果如表3所示。查全率也没有随着T值的增大有多大变化,保持在95%左右,而查准率提升了4%,当T=4时达到了最高的准确率96.02%,每个通道的正确率也都超过了94.25%。

表2 在CASIA1数据集上的实验结果 (%)

表3 在CASIA2数据集上的实验结果 (%)

与其他方法检测结果的对比如表4所示。本文的方法与文献[2]、[8]、[15]、[16]的方法进行对比，均高于其他方法。本文方法在三个公开数据集上都取得了较好的结果。

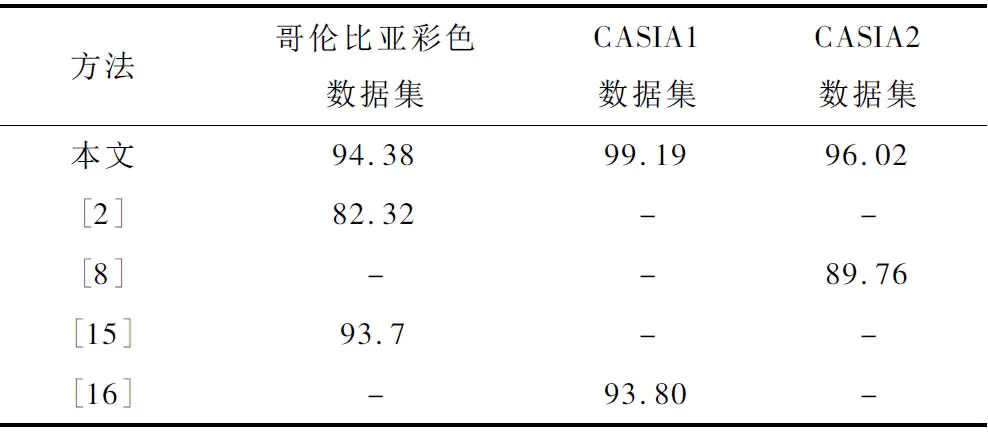
表4 与其他方法检测结果的对比 (%)

2.3 在IFS-TC数据集上进行测试

为了评估算法的有效性，在IEEE IFS-TC第一阶段图像取证竞赛数据集(IFS-TC)上进行测试。数据集包括1 050张原始图像和1 150张篡改图像，图像大小都大于1 024×786。阈值T取值同上文。用同上文一样的分类方法，用SVM分类器进行六倍交叉验证，共进行30次独立的随机实验，取平均结果作为实验结果。评价指标也同上文一致。实验结果如表5所示。当T=3时可以达到92.23%的准确率，单独一个通道的正确率也达到90.91%。从实验结果可以看出，本算法具有良好的性能。

表5 在IFS-TC数据集上的实验结果 (%)

3 结论

本文提出了一种适用广泛的用于拼接检测的马尔科夫特征。在提取特征过程中，只提取了更能反映出拼接痕迹的水平、垂直两个方向的差分矩阵与转移概率矩阵。简单的求和操作不仅使特征维度降低同时更有利于正确分类。提取的改进特征在三个公开数据集哥伦比亚彩色图库、CASIA1和CASIA2上的准确率分别达到了94.38%、99.19%、96.02%。此外，在IFS-TC数据集上也取得了不错的结果，准确率也达到了92.23%。可以看出，不同的数据集的最优参数是不同的，综合来看T=3时在多个数据集达到了最好的效果，特征维度仅为98维，准确率也很高。