固着液滴的流固耦合模态仿真分析
石广丰 霍明杰 王子涛
(长春理工大学 机电工程学院,吉林 长春 130022)
随着社会工业的发展,广为应用的光学变焦系统对高性能变焦透镜的需求越来越大,液体变焦透镜[1]可以很好地弥补传统变焦系统的不足完成其难以实现的功能,它通过改变液体表面曲率、液体折射率、介质上电润湿液体接触角达到改变焦距的目的。其中,利用声场激发液滴振动改变液滴表面曲率的方式,成为提高液体透镜拍摄速度最具有前景的方法之一[2]。因此,研究液滴的共振频率和共振振型具有至关重要的工程应用意义。然而,目前国内外对于流体模态分析的有限元仿真方法尚不成熟,对于流体模态分析仿真,大都采用将流体近似等效为弹性体的方法[3- 4]。这种传统方法会导致以下问题:①液体本身没有泊松比和弹性模量,强制赋予液体实验的近似参数,由于液体工况环境的复杂性,材料参数的时变性,材料参数的近似会引起结果的巨大偏差;②将液体处理为弹性体,忽略了液体的表面张力,但表面张力在流体动态特性分析中起着至关重要的作用。
为此,文中利用有限元仿真分析软件建立固着液滴的有限元模型,对固着液滴进行三维特性分析,通过固着液滴的模态分析得到其固有频率及其对应的固有振型;最后对仿真模态下的特征振型与试验特征模型图[5]、固有频率和质心最大改变量理论值与仿真值进行分析比较,以验证本建模分析方法的准确性。
1 固着液滴理论建模方法
Rayleigh[6]在1879年推导出无束缚、无黏液滴在微小振幅振动时的固有频率和振型,之后Lamb[7]推导出黏性自由液滴的振荡模态。Trinh等[8]利用不混溶液滴实验证明了Rayleigh的预测,Anilkumar等[9]在微重力下利用自由液滴证明了Rayleigh预测。Rayleigh对于自由振荡液滴的预测,对不完全自由振荡液滴的理论计算也具有极大的指导意义,如悬浮液滴、混溶液滴或者附着在固体上的液滴[10- 13]。Strani等[14]推导出一个描述固着液滴共振频率的理论模型,并利用矩阵定义了接触角的本征值。
在毫米级的液滴中,早期的理论研究主要考虑了表面张力和惯性力的影响,而忽略了流体黏性的影响。基于Rayleigh特征自由振荡球形液滴的固有频率为
(1)
式中,σ为表面张力,R为未变形球形液滴的半径,ρ为液滴密度,n为阶数(n=0,1,2,…)。
根据文献[15]得到固着液滴的动态特征方程为
(2)
(3)
μ=h/Ref
(4)
式中,p0为液面处压力,ρe为液滴表面外流体密度,ρi为液滴表面内液滴密度,Pk为勒让德多项式,h为固着液滴的球冠高度,Ref为固着液滴与基面接触的圆面的有效半径。
由于解析求解过程复杂,不能准确、全面地反映求解结果,因此文中采用有限元建模仿真的方法研究固着液滴的动态特性问题。
2 有限元模态分析
2.1 固着液滴的有限元模型
固着液滴模型初始状态的球冠为曲率较大的自由曲面,为了保证模型的连续性和完整性,文中直接在经典ANSYS中建立有限元模型,同时为了减少计算量,将液滴附着的基板简化,基板厚1.00 mm,长和宽均为8.00 mm,半球液滴半径为2.12 mm,如图1所示。
2.2 单元类型及材料参数的选取
文中采用Solid185、Shell181、Fluid30三种不同类型的单元:选用Fluid30流体介质单元划分液滴结构,用该单元模拟液体内部惰性和液体黏度;选用Shell181壳单元划分薄膜结构,特别设置壳单元的劲度、积分项和本构参数,用于表征自由界面的表面张力;选取Solid185固体单元划分基板结构,用该单元模拟液滴固着的板材。将Shell181壳单元的劲度设置为弯曲和薄膜属性,积分项选择缩减积分项,本模型中将壳单元设置为节点等厚度,壳单元厚度设置为整体球冠高度的4%(经多次对比分析拟定的壳单元厚度);根据文献[16]和建模的实际参数,在有限元建模过程中设置阻尼比为0.002。同时,将流体介质单元与壳单元结构进行节点流固耦合设置。有限元模型的材料参数见表1。

图1 固着液滴建模示意图Fig.1 Schematic diagram of sessile droplet modeling
表1 固着液滴有限元模型的材料参数
Table 1 Material parameters of the finite element model of sessile droplet
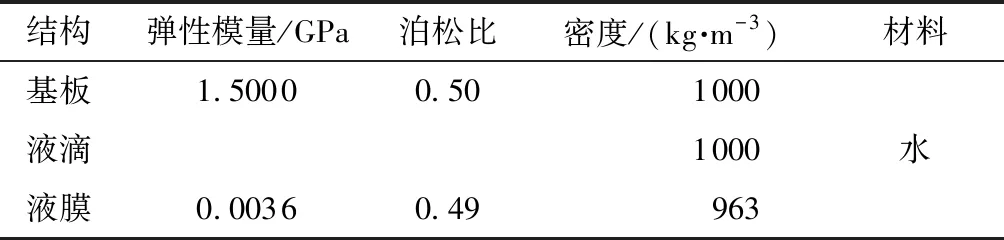
结构弹性模量/GPa泊松比密度/(kg·m-3)材料基板1.50000.501000液滴1000水液膜 0.00360.49963
2.3 网格划分
由于液滴和薄膜的形状复杂,曲率变化大,节点梯度变化剧烈,四面体非结构化网格比六面体结构网格具有更好的适应性和收敛性,更适合固着液滴的网格划分,因此文中采用四面体非结构化网格划分固着液滴。同时,为了保证流体和固体两相接触边界的节点数一致,两相交界面上力-位移的相互传递,模态分析的收敛性和准确性,基板同样采用四面体非结构化网格进行划分,始终保持流固边界在一个时间步长内的移动距离小于一个网格尺寸,即
(5)
式中,时间步长Δt取为0.1 ms,Δtint是流体和固体两相边界移动一个最小网格尺寸所需的理论时间,v是边界移动速度,c是最小的网格尺寸。确定的最小网格尺寸如表2所示。
考虑到基板的粘附作用对液滴产生的固着影响,在基板网格和固着液滴网格之间设置流固耦合边界条件,完成流体域和固体域之间力与位移的相互传递。选取固着液滴的球形液冠表面,利用已有网格属性和材料设置生成一层类薄膜Shell单元,模拟液滴的表面张力。
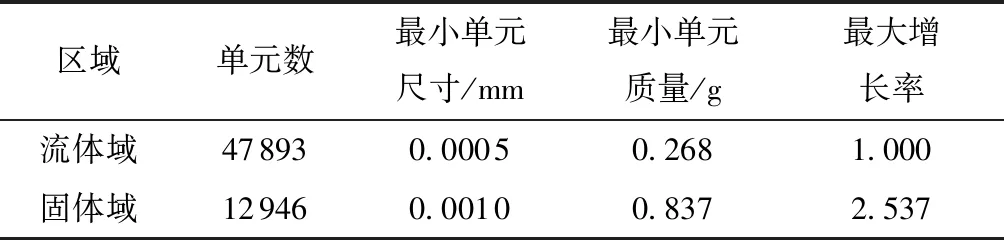
表2 流体域、固体域的网格划分参数Table 2 Meshing parameters of fluid and solid areas


图2 基板、液滴及完整模型的有限元网格模型
Fig.2 Finite element meshing of base,plate droplet and whole model
2.4 计算求解与对比分析
通过模态分析,可以确定模型的频率响应和固有振型。由于本模型涉及流体,故选用非对称法提取六阶模态,频率可用范围为5~200 Hz。所得到的六阶模态频率见表3。
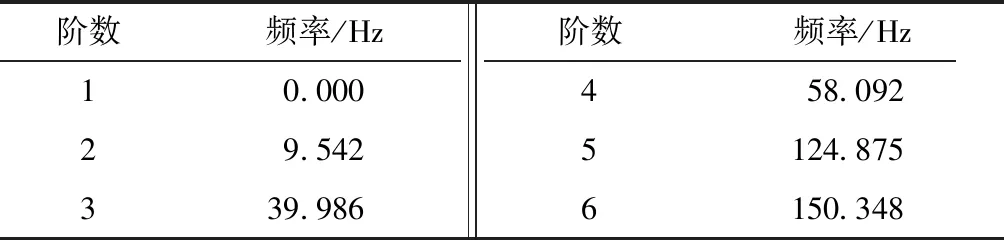
表3 模态分析得到的固有频率Table 3 Natural frequencies obtained from the modal analysis
为了验证仿真方法的准确性,采集固着液滴前几阶特征振型对应的固有频率,与采用Rayleigh模型计算得到的固有振型进行比较。在Rayleigh模型中,n=0和n=1时的共振频率是分别根据体积守恒原理和平移不变原理得出,因此固着液滴的共振频率为0。文中将固着液滴2~5阶Rayleigh理论固有频率与仿真固有频率进行拟合分析,结果如图3所示。由于固着液滴受到基面的粘附力作用,不是完全理想的Rayleigh模型;Bostwick等[17]证明了受束缚液滴的固有频率比无束缚液滴的固有频率大。因此,固着液滴的固有频率应该高于根据Rayleigh理论计算得出的固有频率。

图3 Rayleigh理论固有频率与仿真固有频率的比较
Fig.3 Comparison of natural frequency between Rayleigh theoretical values and simulated values
从图3可知:利用文中的固着液滴建模仿真方法提取到的2~5阶固有频率都大于根据Rayleigh理论计算得到的固有频率,与 Bostwick等[17]的理论计算结果相符;在n=2,3和μ>0的情况下,固有频率在接近μ=0.5时会出现峰值;当n=4,μ>0时,有两个明显的峰值点,分别在μ=0.4和μ=0.7附近;当n=5,μ>0时,其峰值达到270 Hz左右。
3 仿真与实验结果的对比分析
3.1 特征振型比对
在Chang等[5]应用正弦波谐振固着液滴的实验中,所取液滴为纯水,体积为20 μL,基板为化学功能化玻璃(表面涂有APTES),主要是为了保证液滴与附着板材之间的接触角始终保持在60°~70°,在仿真中利用约束接触线来控制接触角的范围;利用信号发生器和功率放大器通过机械振荡器生成正弦波激励固着液滴,用一台高速摄像机捕获固着液滴的立体图像,搭建一个能够捕获上视图和左右视图的观测台,如图4所示。为每一个图像设定一个条件环境,并且记录200个连续帧。在该实验模型的透明玻璃下面贴着网格大小为50 μm的金属网,金属网格是通过上视图能够分辨网格变形的关键,如图4所示。
文中通过ANSYS APDL有限元分析软件,应用上述方法进行固着液滴的三维建模及有限元模态分析仿真,得到固着液滴的各阶固有振型谱图,如图5所示,同时给出了文献[5]中实验得到的固着液滴振型谱图。从图中可知,有限元模态分析得到的固有振型谱图与文献[5]得到的实验振型谱图吻合度较高。
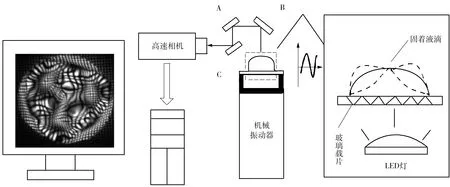
图4 文献[5]应用正弦波谐振固着液滴的实验装置Fig.4 Experimental device of applying sine wave to resonant sessile droplet in reference[5]




图5 提取特征模态振型的实验数据与有限元仿真结果对比Fig.5 Comparison of extracting characteristic mode shapes between experimental data and finite element simulation results
由单个振动周期内的等值线云图可知,固着液滴在一定激励下,该阶模态中各个部分的位移情况(这里显示的只代表相对大小,不是实际位移值),可以由仿真软件三维动态图观察整体振型。观察网格变形图,能够发现各阶振型的特征以及液滴表面各处的曲率变化,从而直观地对比仿真网格与实验中金属网格变化规律的异同点。利用速度矢量图,能够观察到固着液滴振动周期内液体的流动方向和运动趋势。
3.2 质心振动最大改变量的比较
因固着液滴与基面接触的有效半径Ref远远小于声源直径,故可以将声波看成平面波。在忽略重力作用及其他能量损失的条件下,声源发出的能量(Eb)应等于液滴表面张力所做的功(Eσ),即Eb=Eσ。给予系统的驱动声波为平面波[15]。液体透镜中液体质心的改变量为
(6)
式中,Rb为底部球缺半径。
固着液滴的共振会引起其质心的变化。换而言之,质心的变化规律在一定程度上反映了固着液滴的振动频率和振幅的规律。文中取μ=1时2~5阶固着液滴的质心振动最大位移的理论计算值与仿真提取值进行比较,结果如表4所示。
表4 质心振动最大改变量的理论计算值与仿真提取值对比
Table 4 Comparison of the maximum change of centroid vibration between the theoretical calculation values and the simulation extraction values

阶数质心振动最大位移/mm理论值仿真值20.080.1030.150.1740.270.3350.810.89
由表4可知,固着液滴质心振动最大改变量的仿真值略大于理论计算值,相对误差不超过25%,并且它们的增长趋势基本相同。随着阶数的增大,固着液滴的质心最大改变量上移,导致固着液滴的振幅不断增大。
以上对特征振型、固有频率和质心最大改变量理论计算值和仿真值的分析比较,说明了应用文中提出的有限元模拟仿真方法研究流体模态是一种非常有效的方法,文中提到的流固耦合分离建模方法和类薄膜结构材料参数设置对于固着流体的模态求解具有很重要的应用价值。
4 结论
文中利用流固耦合分离建模方法对固着液滴进行有限元建模及分析,将流体的表面张力等效成类薄膜结构,并利用ANSYS APDL中的节点流固耦合方式模拟液滴与基面的粘结作用。模拟实际的工况条件,给定结构约束和耦合约束,得到固有频率、特征振型和质心最大改变量的仿真数值,然后比较仿真数值与理论数值,结果表明:液滴2~5阶的仿真固有频率均大于根据Rayleigh理论计算得到的结果,符合现有文献的理论证明结果;有限元仿真得到的固着液滴四阶振型谱图与现有文献得到的实验振型谱吻合;质心振动最大位移仿真值与理论计算值的相对误差不超过25%。今后可以通过研究声学激励后液滴形态的变化规律,优化液滴搭载平台,制作体积小、成本低、可靠性高的高速变焦液体透镜。

