基于液压变压器的直线执行机构的节能研究

姜继海 杜治 沈伟 沈超

(1.哈尔滨工业大学 机电工程学院，黑龙江 哈尔滨 150080；2.浙江大学 流体动力与机电系统国家重点实验室，浙江 杭州 310027；3.上海理工大学 机械工程学院，上海 200093)

随着社会经济的飞速发展，能源短缺、环境污染问题愈发突出，为实现可持续性发展，节能减排逐渐成为每一个行业技术发展的首要任务[1- 2]。液压系统的工作环境恶劣，效率不高，液压元件的工作稳定性易受工作条件的影响，极大地限制了液压传动技术的应用和发展[3- 4]。恒压网络(CPR)通过控制二次元件实现向负载输送能量和回收负负载能量，可并行连接多个不相关的负载以实现不同的控制策略，进而实现功率适应，在节能方面具有很大的优势[5- 6]。尽管CPR具有众多优点，但对于执行机构为液压缸的系统，由于其很难改变液压缸的有效作用面积，所以往往因采用节流阀实现控制而造成了节流损失，且不能回收再利用负负载能量[7- 8]。因此，CPR急需一种能够无节流损失控制直线执行机构速度的执行元件，液压变压器就是在这种应用背景下出现的。

传统液压变压器是把两个轴向柱塞元件通轴连接，通过改变排量的方式实现变压功能，但由于体积大、效率较低，导致其应用较少。新型液压变压器以轴向柱塞元件为基础元件，集液压泵/液压马达功能于一体设计而成。新型液压变压器与传统轴向柱塞泵/马达的主要区别在于配流盘的结构形式不同。自1997年Inna公司设计加工第一台新型液压变压器(HIT)[9]以来，国内外研究学者在新型液压变压器结构、应用等方面开展了广泛深入的研究。2000年，Achten等[10- 11]针对液压变压器配流盘受力不均匀的问题，设计了配流盘结构，改善了液压变压器的控制性能；2002年Malsen等[12]通过实验证明了采用“梭”的IHT具有良好的减噪效果；2009年，Achten等[13]设计加工出旋转斜盘式液压变压器，并成功应用于一辆液压混合动力汽车中，结果显示燃油消耗率降低了50%。

目前，国内外研究主要集中于提高液压变压器元件的性能，应用研究主要集中在混合动力车辆上，对于采用新型液压变压器的回收直线执行机构负载重力势能方面的研究很少。为了提高能量利用效率，文中拟对采用新型液压变压器的直线执行机构回收负负载能量的过程进行研究，建立系统的数学模型，并进行仿真分析。

1 液压变压器简介

新型液压变压器的配流盘截面如图1所示[14]。3个配流口分别连接恒压油源、负载以及油箱，可通过调整3个配流口相对于上下死点的相对转动角度来实现“变压”功能。

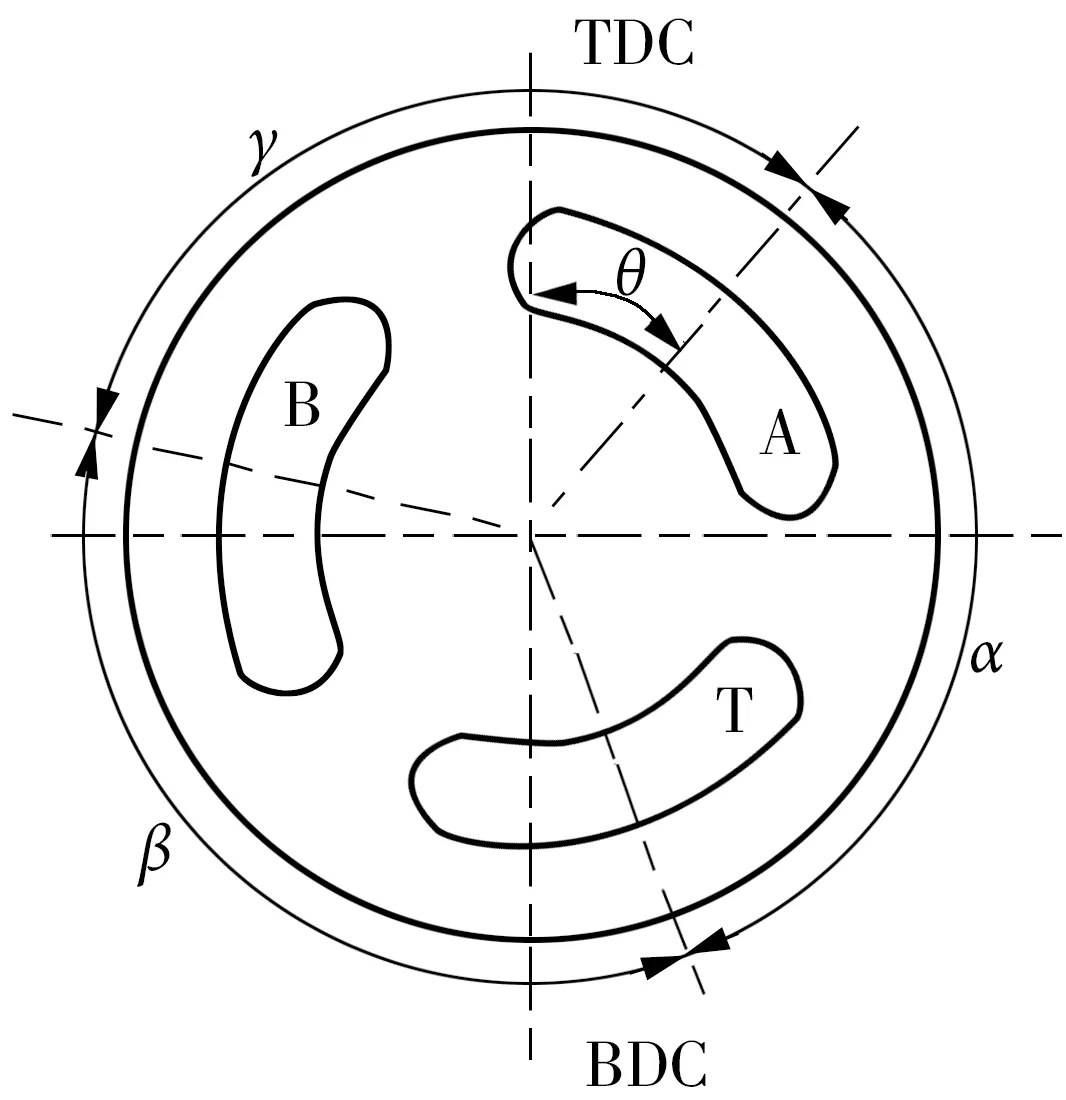
图1 新型液压变压器的配流盘截面简图[14]

Fig.1 Schematic diagram of the valve plate of new hydraulic transformer

当液压变压器处于稳定工作状态时，由A、B、T端口液压油产生的平均转矩的合力矩为0，即TA+TB+TT=0，因T端口一般与油箱连接，故其压力pT为0。新型液压变压器的变压比为

(1)

式中，α、β为常数。新型液压变压器变压比可以看作是控制角θ的函数，改变θ则可以改变变压比。

2 节能系统理论分析

节能系统的能量回收过程示意图如图2所示。当负载从高处下降时，液压缸有杆腔输出压力油作用在液压变压器B端口使缸体反转，从A端口输出的油液流进蓄能器中存储起来，实现能量回收。

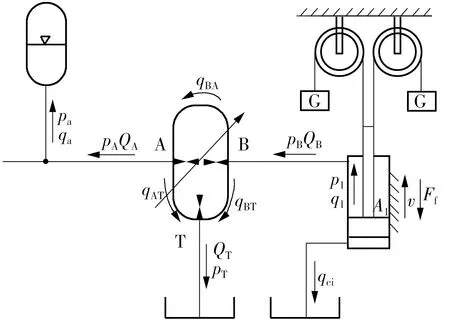
图2 节能系统示意图Fig.2 Schematic diagram of energy saving system

液压缸的力平衡方程和流量连续性方程为

(2)

(3)

式中：m为负载盘以及负载的总质量，kg；p1为液压缸有杆腔的油液压力，Pa；A1为液压缸有杆腔的有效面积，m2；v为负载的运动速度，m/s；Bc为缸筒和活塞间的阻尼系数，N/(m·s-1)；Ff为缸筒和活塞杆间的动摩擦力，N；q1为液压缸有杆腔的流量，m3/s；Lci为液压缸的内泄漏系数，m3/(s·Pa)；V1为液压缸有杆腔的体积，m3；βe为介质的体积弹性模量，Pa。

由于液压变压器T端口与油箱相连接，扭矩为0，因而可以得到A、B端口的流量连续性方程和扭矩方程为

Lti(pB-pA)+Lti(pB-pT)+LtepB

(4)

Lti(pA-pT)-LtepA

(5)

(6)

(7)

式中：QB为流进B端口的流量，m3/s；QA为流出A端口的流量，m3/s；Lti和Lte分别为液压变压器的内泄漏系数和外泄漏系数，m3/(s·Pa)；ωHT为液压变压器缸体的角速度，rad/s；VHT为液压变压器的排量，m3/r；pA、pB和pT分别为A、B、T端口的油液压力，Pa；θ为斜盘转角，°；α、β、γ分别为A、B、T端口的包角，°。

机械摩擦扭矩Tfr和粘性摩擦扭矩Tfv可表示为

Tfr=Cr(TA+TB)

(8)

Tfv=CvωHT

(9)

式中：Cr为液压变压器各槽口的机械摩擦系数；Cv为粘性摩擦转矩系数，N·m/(rad·s-1)。

回收能量过程中作用在液压变压器缸体上的合扭矩为

(10)

文中回收能量过程采用气囊式液压蓄能器，其在工作过程中遵循气体的玻意耳定律，即

(11)

式中：pa0、pa1、pa2分别为气体的预充气压力、最低压力、最高压力，Pa；pa为气体在任意状态下的压力，Pa；Va0、Va1、Va2分别为预充气压力、最低压力、最高压力对应的气体体积，m3；Va为气体任意状态下的体积，m3；n为气体多变指数，取为1.4;const为常数。

节能系统在能量回收过程中的总效率为液压变压器效率和液压缸系统工作效率的乘积，即

(12)

节能系统能量回收过程中的总效率与负载运动速度和斜盘转角之间的等效率曲线如图3所示。由图中可以看出，节能系统的能量回收效率最高可以达到60%，而且高效区所对应的液压缸运动速度和斜盘转角运动范围很大，有利于在回收能量过程中更好地控制液压变压器，使其与液压蓄能器协调工作，使节能系统的能量回收效果达到最好。

根据图3，要使系统回收的能量最多，需保证系统能量回收效率为60%，此时对应的负载运动速度在200～600 mm/s之间，在此运动速度范围内，每个运动速度对应一定的斜盘转角范围及变压比范围，分别如图4所示。

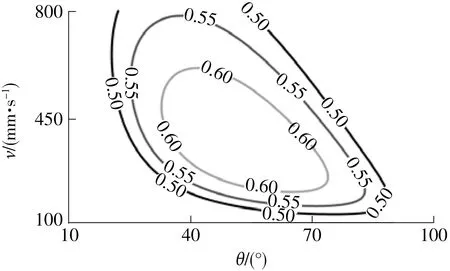
图3 节能系统的等效率曲线Fig.3 Equal efficiency curves of energy saving system

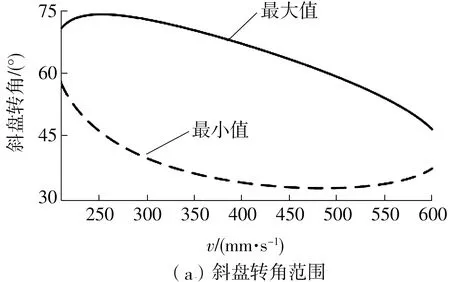
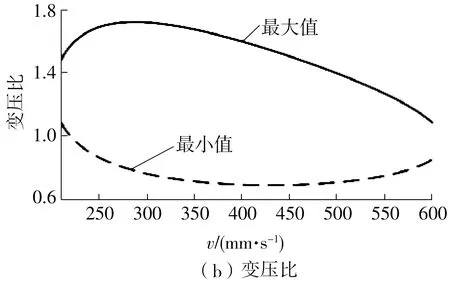
图4 负载运动速度对应的斜盘转角范围和变压比曲线

Fig.4 Angle range of swash plate and curve of transformation ratio corresponding to load moving speed

当节能系统的能量回收效率确定后，蓄能器所能存储的能量Ea是定值，因而可以得到液压蓄能器容积与其初始压力和最终工作压力的关系式：

(13)

液压变压器B端口的压力pB与pa0和pa2的比值即为回收能量过程中液压变压器的初始变压比Π0和最终变压比Π2，因而可以将式(13)变换为

(14)

通过优化算法的计算，可以得到液压蓄能器的容积Va0的最小值随着负载运动速度的变化曲线，如图5所示。由图中可以看出，液压蓄能器容积范

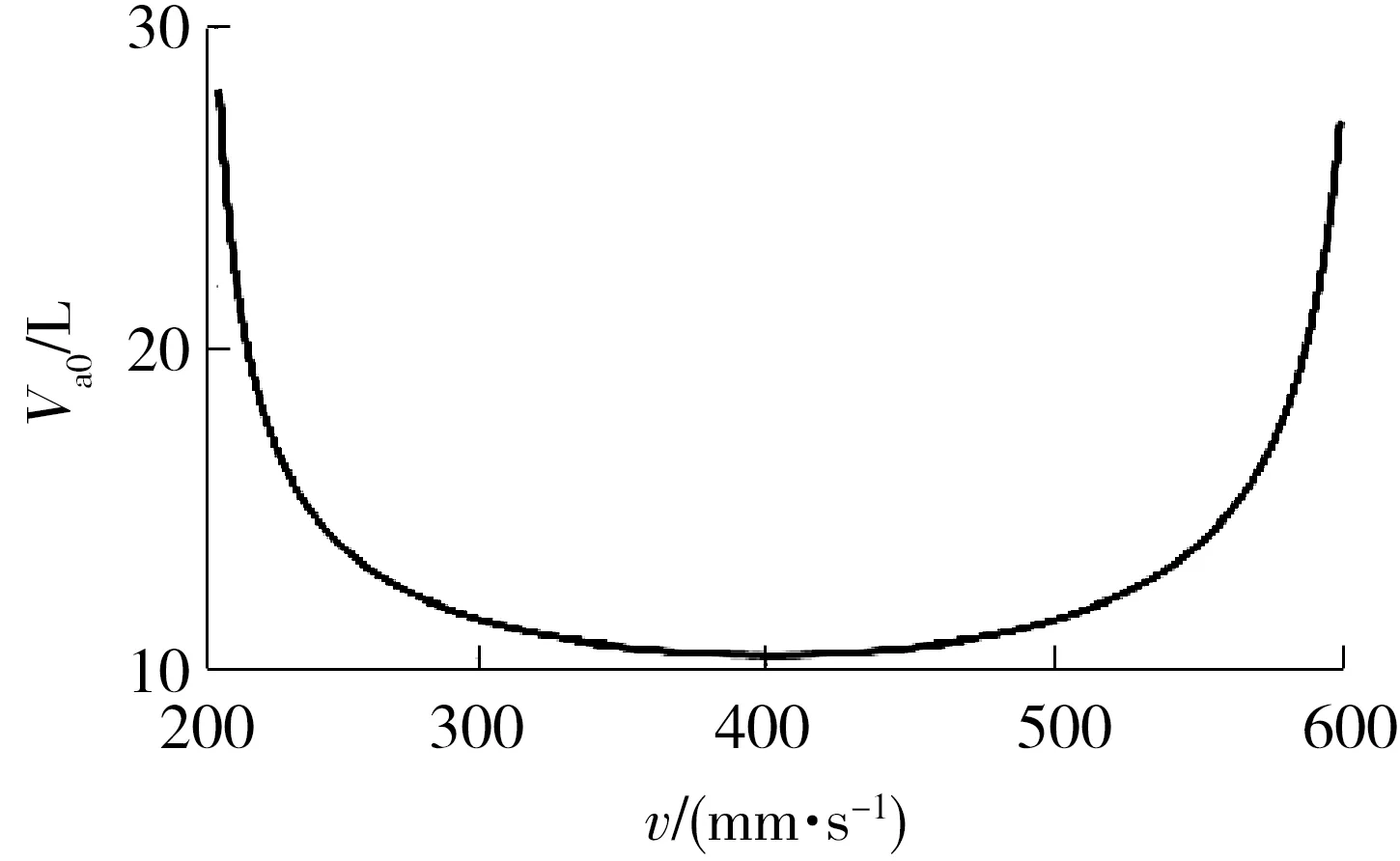
图5 液压蓄能器容积的最小值曲线Fig.5 Minimum value curve of hydraulic accumulator volume

围为10～28 L，根据国家标准，NXQ型液压蓄能器的公称容积有16 L和25 L可以满足要求。当容积为16 L时，7 500 kg的负载回收能量结束后液压蓄能器的压力变化范围较大，会使系统泄漏增大，效率降低，因而文中选择液压蓄能器容积为25 L，其对应的负载运动速度范围为210～590 mm/s。

运动速度范围中每个运动速度对应的变压比范围不同，因而液压蓄能器中的初始压力和最终压力都会变化，经计算可以得到回收能量过程中液压蓄能器初始压力和最终压力的变化曲线，如图6所示。图中曲线1和2所组成的区域为液压蓄能器初始工作压力可选的范围，而曲线3和4所组成的区域为最终工作压力的范围。由于液压蓄能器与恒压变量泵共同组成恒压网络为系统供油，因而液压蓄能器的初始工作压力即为恒压网络的供油压力。NXQ型液压蓄能器的公称压力为31.5 MPa，因而液压蓄能器的最终工作压力不能超过该值。根据图6可知，液压蓄能器的初始压力不能低于15 MPa，因而初步选择恒压网络压力为16 MPa，负载运动速度为350 mm/s作为仿真研究的参数，回收能量结束之后液压蓄能器的压力约为23 MPa，低于其公称压力。

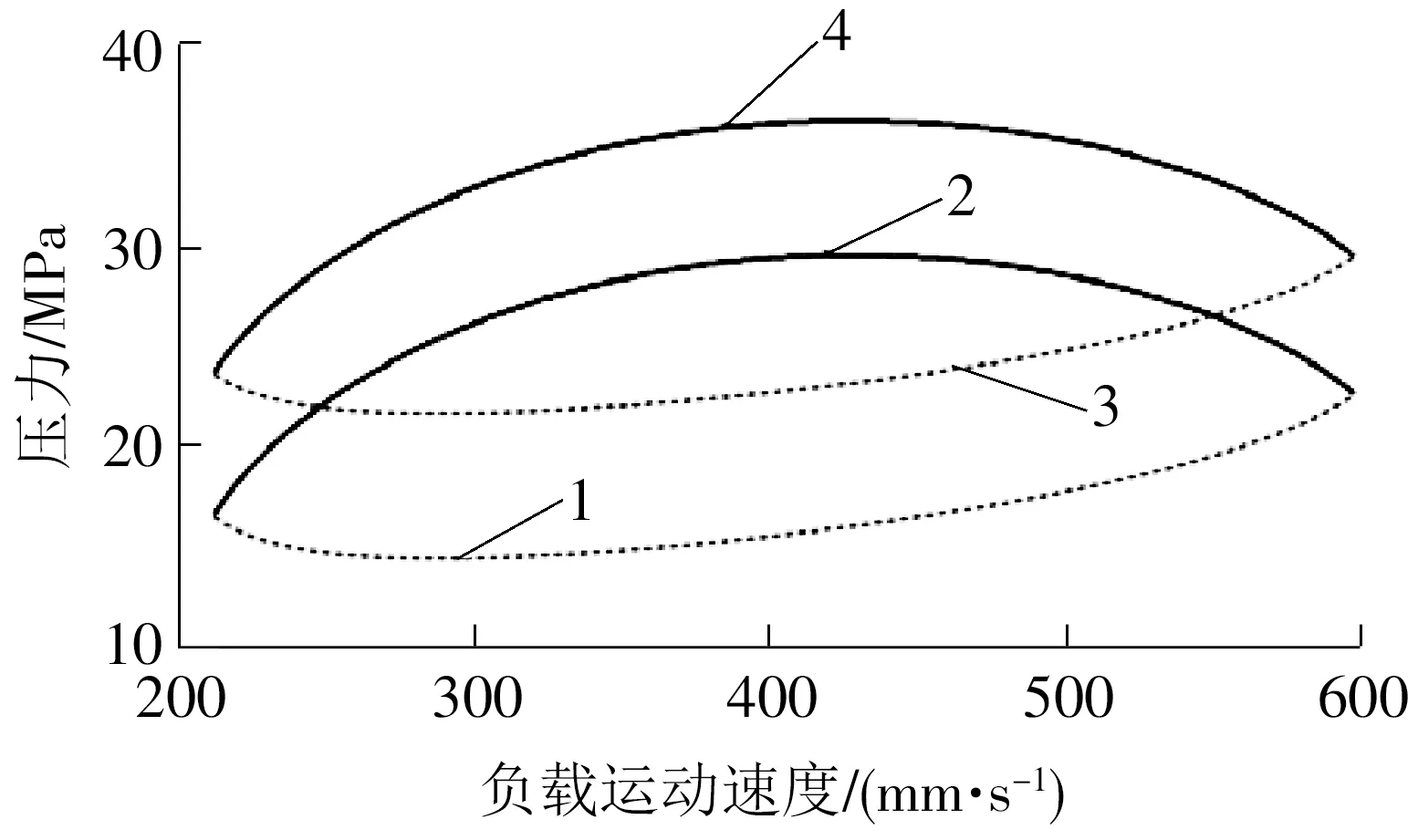
图6 液压蓄能器的压力变化曲线Fig.6 Pressure change curves of hydraulic accumulator

3 节能系统仿真

根据式(5)-(13)，选择状态变量：

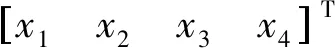
因而，可以建立系统的状态空间方程为

由于节能系统具有很强的非线性特性，传统PID控制难以实现对负载运动速度的控制，当速度不稳定时，节能系统很有可能不是工作于高效区，导致回收能量的效果变差，因而文中采用模糊PID控制策略来实现对负载下降时运动速度的控制，以保证节能系统的能量回收效率。采用模糊PID控制的节能系统框图如图7所示。

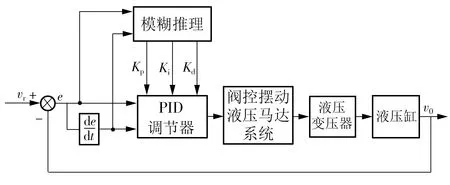
图7 节能系统控制框图Fig.7 Control block diagram of energy saving system

在图7中，模糊PID控制器的控制算法为

其中，Kp、Ki、Kd的调整算法为

设置模糊控制器的输入变量e和ec及输出变量Kp的论域均为{-3，-2，-1，0，1，2，3}，输出变量Ki、Kd的论域分别为{-1.00，-0.67，-0.33，0.00，0.33，0.67，1.00}和{-0.3，-0.2，-0.1，0.0，0.1，0.2，0.3}。

输入变量e和ec以及输出变量ΔKp、ΔKi和ΔKd的隶属度函数均选择为三角形函数，如图8所示。

通过分析PID参数变化对系统响应的影响，以及许多工程人员的技术总结和实际操作经验[15]，可以得到Kp、Ki、Kd的模糊控制规则，如图9所示。

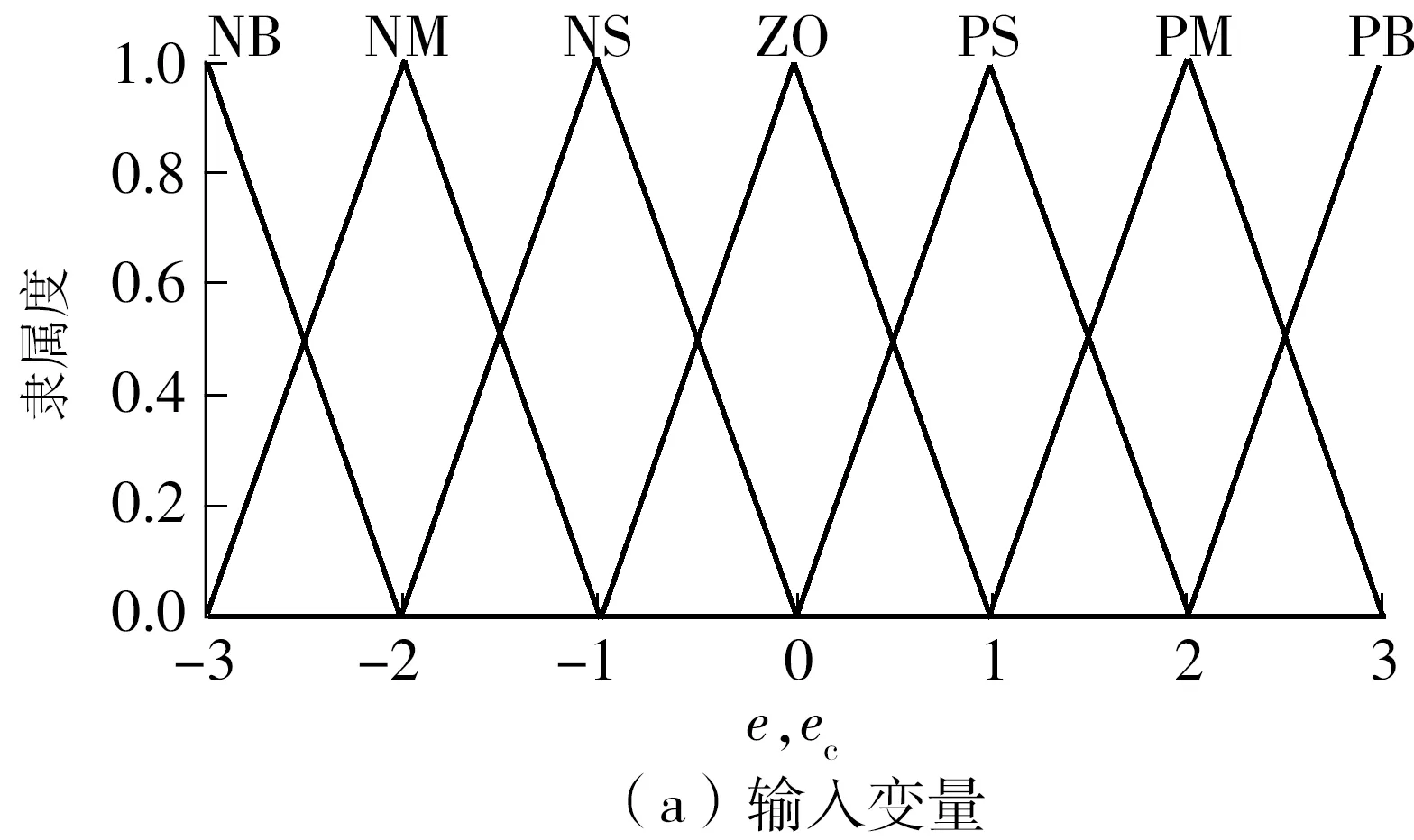
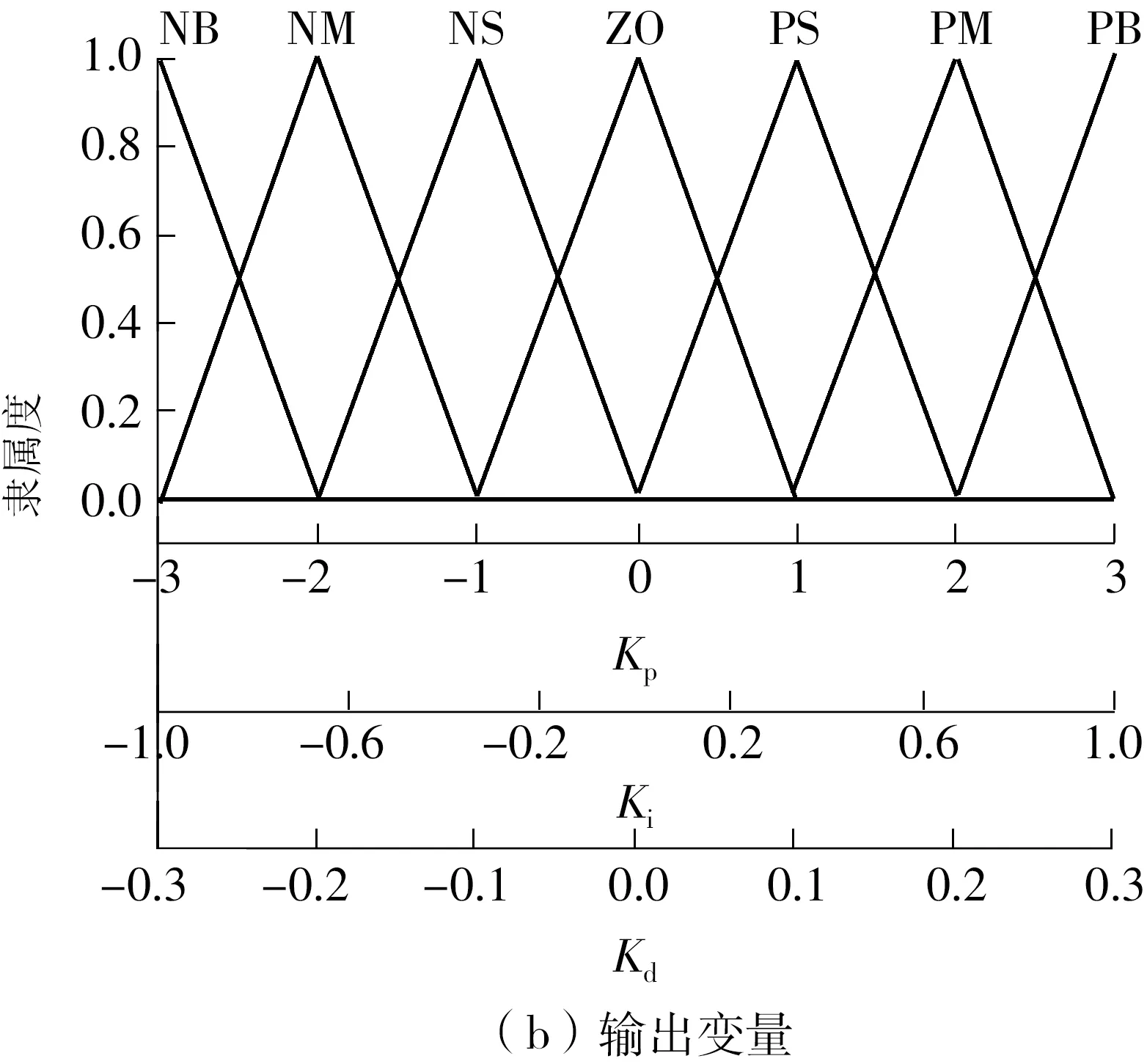
图8 输入变量和输出变量的隶属度函数Fig.8 Membership function of input and output variables

模糊控制器的解模糊算法选用重心法，可以建立以理想速度为输入、负载运动速度为输出的节能系统的Simulink仿真模型，如图10所示。通过仿真，可以得到模糊自整定PID控制和常规PID控制下负载的运动速度输出曲线，如图11所示。

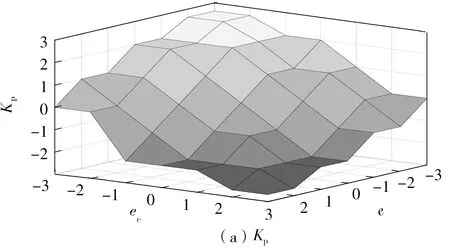
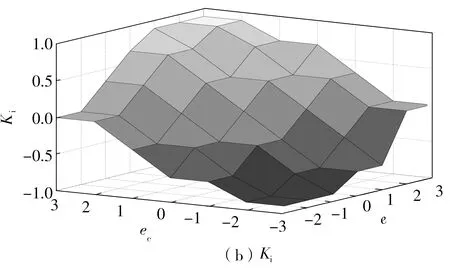
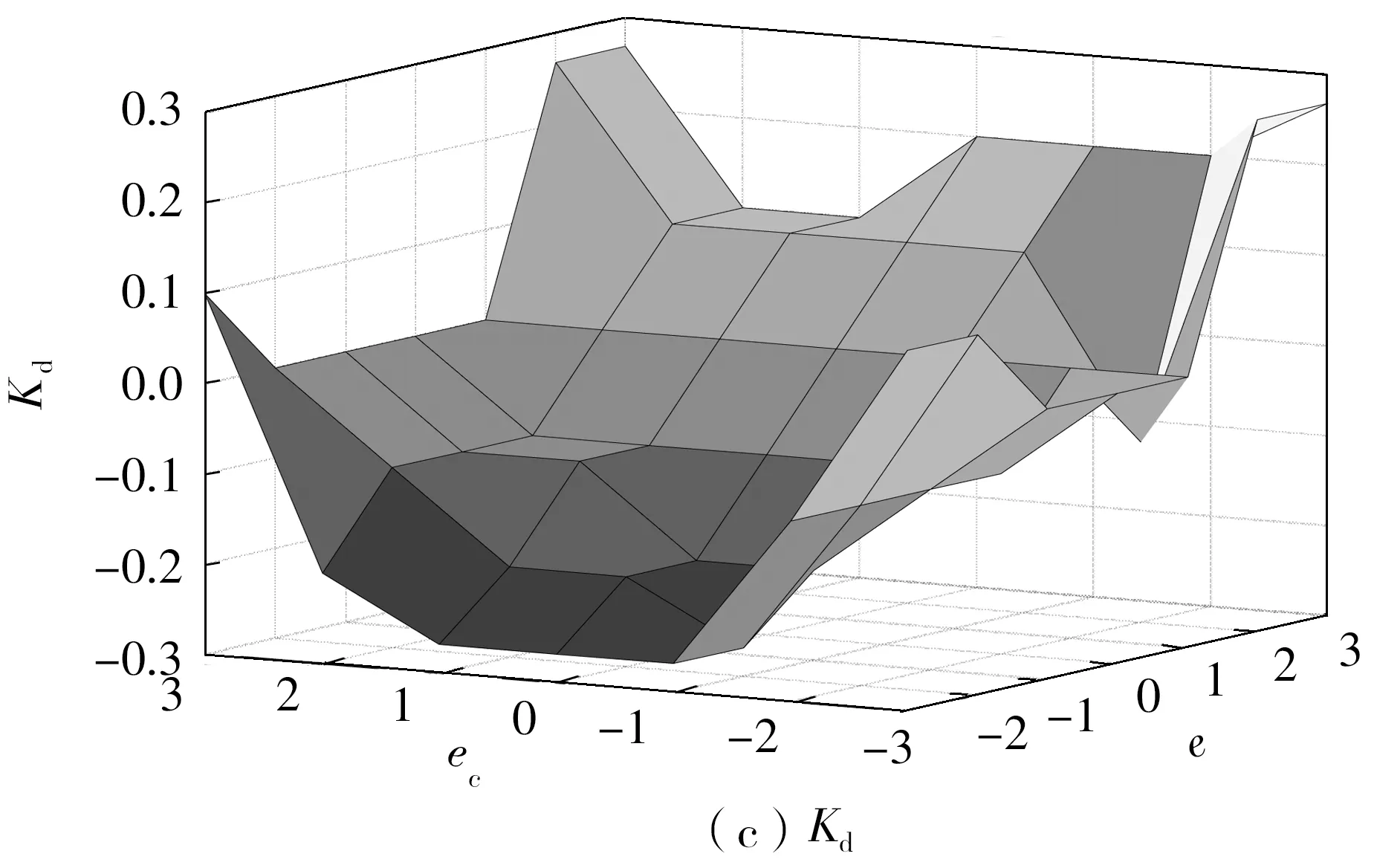
图9 Kp、Ki、Kd的模糊控制规则Fig.9 Fuzzy control rules of Kp，Ki and Kd

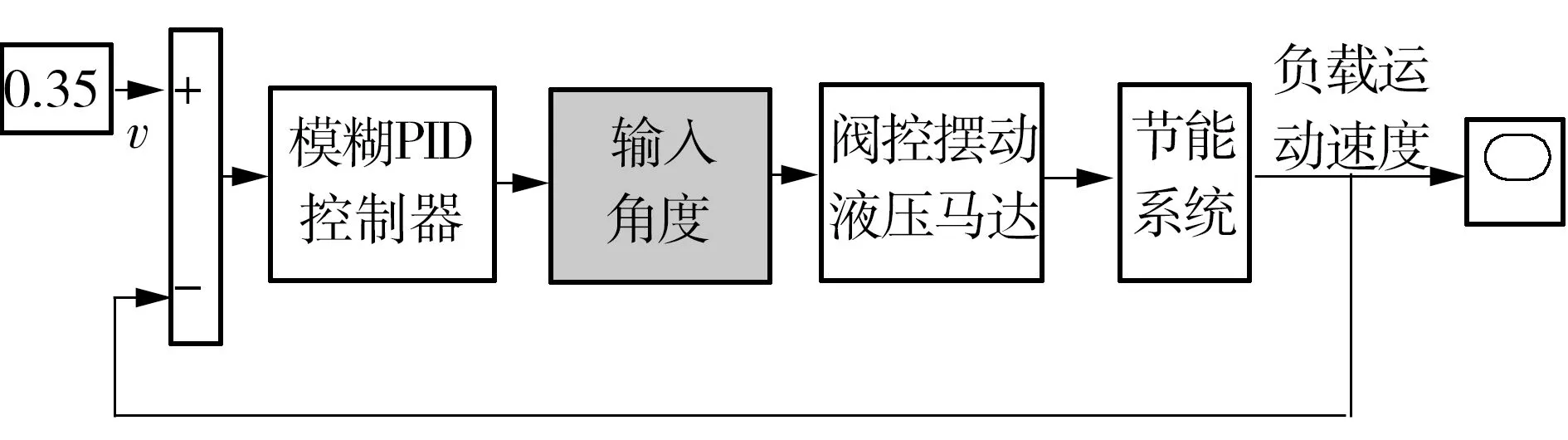
图10 节能系统的仿真模型Fig.10 Simulation model of energy saving system

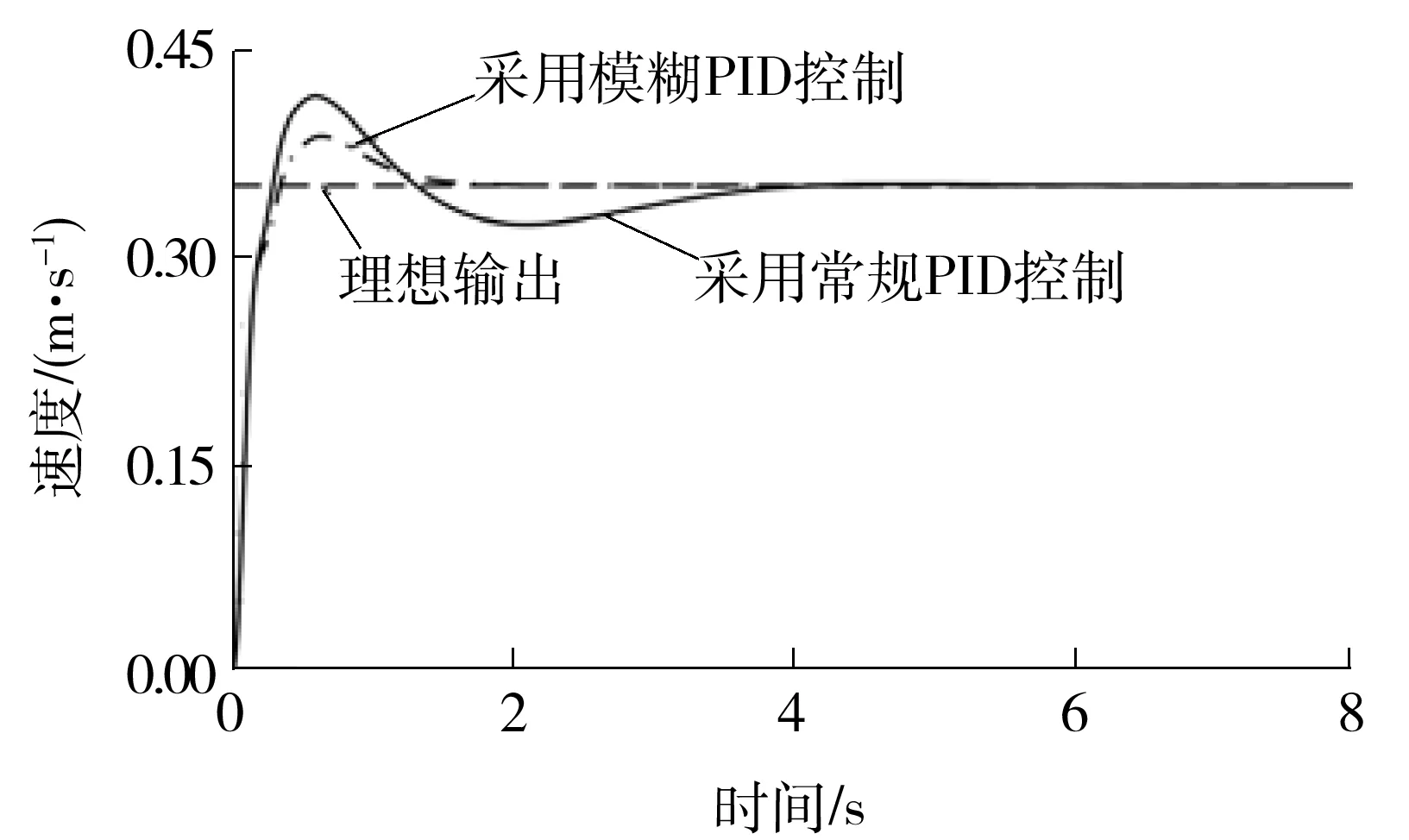
图11 负载运动速度响应曲线Fig.11 Speed response curve of load movement

由图11可以看出，与采用常规PID控制的节能系统相比，采用模糊自整定PID控制的节能系统的输出曲线的超调量和调整时间均有了显著的改善，说明模糊自整定PID控制算法在回收能量的过程中可以很好地对负载的运动速度进行控制。

液压蓄能器中气体压力的变化曲线如图12所示。文中所用的液压缸位移为2.5 m，当负载运动速度为0.35 m/s时，需要7 s左右即可完成回收能量的全过程。在回收能量的过程中，液压蓄能器的气体压力从初始时的16 MPa开始增大，在7 s时达到23.3 MPa，所回收的能量约为1.1×105J，能量回收效率约为59.86%，与理论分析结果基本一致。

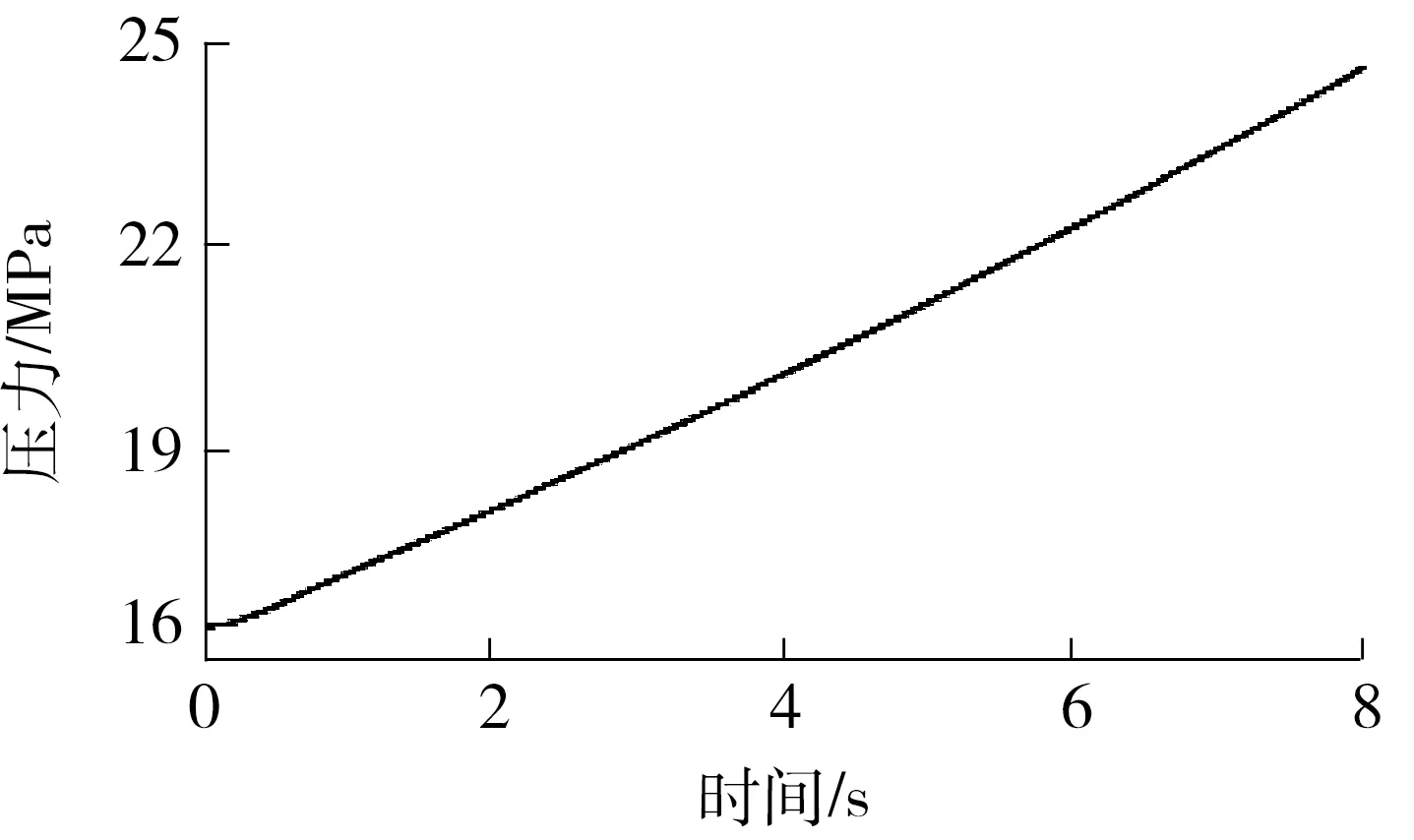
图12 液压蓄能器压力的变化曲线Fig.12 Pressure change curve of hydraulic accumulator

4 结论

(1)所建立的节能系统的效率最高能够达到60%，而且高效区所对应的斜盘转角和负载运动速度范围很大，有利于节能系统工作时液压变压器与液压蓄能器更好地协调工作，使系统的回收效果达到最好；

(2)节能系统具有很强的非线性，所提出的模糊PID控制策略能够很好地实现对负载下降时运动速度的控制，显著改善了系统的输出响应。