浅谈系统论、信息论、控制论对数学教学的启示

张镡文

【摘要】依据系统论、信息论和控制论的基本思想，探讨系统论、信息论、控制论对数学教学设计和教学过程调节的启示.

【关键词】系统论;控制论;信息论;数学教学

一、系统论、信息论和控制论的基本内容

（一）系统论

1932年，美籍奥地利生物学家L.V.贝塔朗菲首次提出“一般系统论”概念，成为系统论创始人.我国著名科学家钱学森认为，系统是由相互联系和相互作用的若干要素结合而成的具有特定功能的整体.比如，教学系统的要素主要包括教师、学生、教材和教育影响.

系统的基本特征有整体性、目的性、动态性、相关性和环境适应性.整体性是系统最基本的属性.系统并不是各个要素功能的简单相加，其整体功能大于组成系统的各部分功能之和.系统中任何一个要素发生变化时，都会影响其他要素和整体功能的发挥.

（二）信息论

1948年，美国数学家申农发表了《通讯的数学问题》一文，标志着信息论的诞生.狭义信息论是一门运用数理统计方法研究信息处理和信息传递规律的科学.信息传递的一般模型如图1所示.

信源即产生信息和信息序列的源头，它可以是人或物.信源编码是将信息数字化的过程，以提高信息的传输效率.信道是信息传输的通道，也即信息传输媒质.信道编码是在信源码中加入纠错码，提高信息在传递过程中的抗干扰能力.信源译码和信道译码则是将被編码的信息还原成初始信息的过程.信宿是信息的接收者.

（三）控制论

1948年，数学家诺伯特·维纳发表了《控制论》一书，标志着控制论的诞生.控制论是研究动物（包括人类）和机器内部的控制与通信的一般规律的科学，是跨及众多学科的交叉学科.

控制论的基本方法有反馈方法、黑箱方法和模拟方法.反馈是指信息从被控制者输出端回输到控制者，并对系统的再输出产生影响的过程.如图2所示.反馈的两个必要条件是准确性和及时性，两者缺一不可.准确性指反馈信息的真实性、可靠性，否则错误的信息将导致错误的决定，从而使控制失效.及时性指信息反馈应在被控系统状态改变之前，否则不能调节下一次控制的反馈信息，再准确也是没有意义的[1].

二、系统论、信息论和控制论对数学教学的启示

（一）系统论对数学教学设计的启示

第一，把握数学知识的整体性

数学是一门逻辑性、结构性非常强的学科.在初中数学教材中，从有理数到实数、一元一次方程到二元一次方程、一次函数到二次函数再到反比例函数等知识，都是螺旋式上升的过程.在此过程中，前面知识是后续知识的基础和铺垫，后续知识又是前面知识的升华.因此，在进行教学设计时，教师不能只关注一个个孤立的知识，而必须理清各知识之间的内在联系，通读教材，充分把握数学知识的整体结构，确保前面基础性知识的学习，为后续知识打好基础，并且在学习后续知识时充分利用学生已有经验，激活学生的思维.

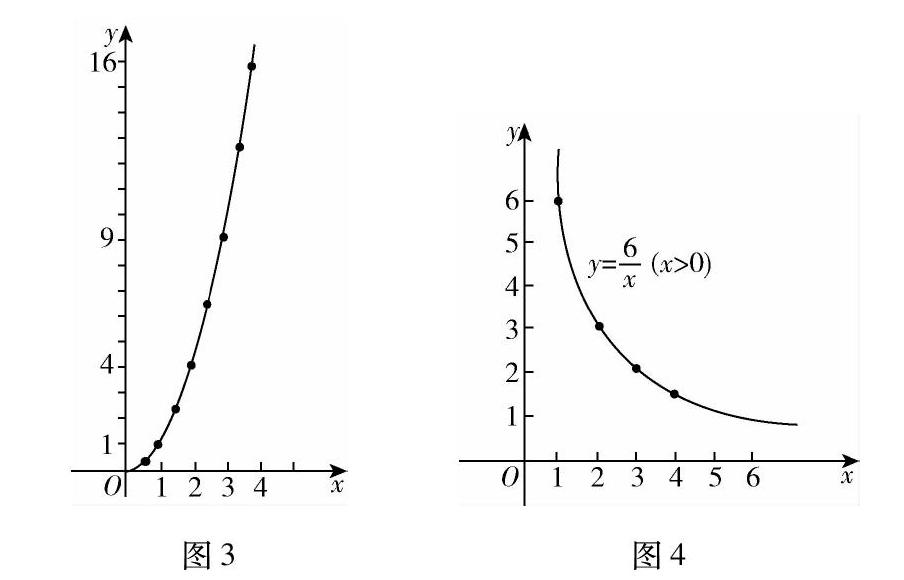
比如，八年级下册第十九章一次函数19.1.2函数图像之中出现了如下的二次函数图像和反比例函数图像（如图3，图4所示）.而二次函数和反比例函数分别是九年级上册和九年级下册的知识点，这两幅图的意义何在呢？显然，编者是想学生在八年级时对二次函数和反比例函数有个初始印象，使这两幅图起到“先行组织者”的作用.当学生到九年级真正接触二次函数和反比例函数时，已有经验就会成为学生搭建新知识的桥梁，促进学生对新知识的理解与内化.因此，教师在设计函数图这节课时，应重视这两幅图像，力求给学生留下深刻印象，不能为赶进度一带而过，导致因小失大.

第二，把握教学过程的整体性

倘若学校是一个交响乐的场所，教学便是师生共同演奏的一篇欢快乐章.显然，教师在教学过程中不是单向传输知识的表演者，而是与学生、教材等要素组成的有机整体.因此，教师在进行教学设计时，还应注重教学过程的整体性.

首先，重视目标对教学过程的调控作用.教学目标是教学的起点和归宿，它影响着教法学法、教学策略、手段和评价等多个方面，对教学过程有着支配和指导作用.因此，教师应时刻牢记教学目标，始终围绕教学目标开展活动.其次，重视教学过程的整体性.目前数学教学普遍存在着“重结果轻过程”的现象，但数学教学传递的不仅仅是一个命题或公理，而是蕴含在命题之中的逻辑思维与数学思想方法.教师要重视教学过程的搭建，处理好知识与能力、结论与过程，以及师生情感等各部分关系.苏霍姆林斯基说：“教学活动的主导是教师在课堂上讲解，但不要总是教师在讲，这种做法不好，要让学生通过自己的努力去理解东西，才能成为自己的东西，才是学生真正掌握的东西.”因此，教师应努力协调导与学、讲与做的关系，适时采用以教师为主导，学生为主体的合作探究教学模式，激起学生学习兴趣，实现教师与学生的共赢.

（二）信息论对数学教学过程的启示

课堂教学是一个信息传递的过程.信源是教材和教师，信源编码和信道编码则是教师精心备课和技巧讲授的过程.

信源编码和信道编码的目的是提高信息的传输效率，增强信息的抗干扰能力.因此，信息传递的量及表示就显得尤为重要.在教学过程中，单位时间内教学信息量过多或过少都会影响教学效果，过多学生不易消化吸收，过少又浪费了学生宝贵的时间.因此，教学信息量的把握至关重要.如何才能恰到好处把握信息量呢？首先，要通读教材和大纲，理清重难点，根据课时合理安排课容量;其次，做好学情分析，根据学生生理、心理、知识基础、能力高低等情况安排课容量;最后，根据学生课堂学习反馈，灵活改变要讲授的信息量.

信息传递的最后环节译码、信宿，仍需教师精心设计.马斯洛需求层次理论提出，自我实现的需要是最高层次的需要，只有当基本需要被满足时人才会产生自我实现的需要，而学习就是自我实现的需要.因此，教师应关心学生的日常生活，使其基本需要得到满足，激起学生学习动机.

（三）控制论对调节数学教学的启示

由反馈方法可知，信息从被控制者的输出端回输到控制者，并对系统的再输出产生影响，从而起到控制的作用，使系统始终处于最优的动态水平，并朝着预定的目标前进.而反馈的两个必要条件是准确性和及时性，教师在教学过程中如何准确及时地获取反馈信息呢？首先是观察，大到课堂气氛，小到学生的表情、神态、动作，尤其是眼神，眼睛是心灵的窗户.其次是提问，提问有两种，一是教师精心设问，既可以了解学生学习情况，又可以切中重难点，诱导学生深度思考;二是学生提问，既可以反映学生对知识的理解程度，又可以培养学生语言表达能力.最后，学生或小组汇报学习成果，并根据强化理论进行适当奖惩，既可以了解学生的学习情况，又可以激起学生学习的积极性[2].

在教学过程中，经常会出现这种现象：当学生的答案不是教师的预设时，教师会略过，甚至置之不理.显然这不利于调动学生学习的积极性，并且显露出教师自身素养的不足.因此，数学教师应树立终身发展观，不断提升自身修养，以至能自如地应对学生的反馈，根据反馈信息及时调整教学容量和教学活动，而不是默守成规，唯教案是从.

【参考文献】

[1]李诚忠，王序荪.教育控制论[M].长春：东北师范大学出版社，1986.

[2]陈锦铎.控制论信息论系统论在教学设计中的应用[J].湖南中学物理，2010（1）：57-58.