液压提升机负载适应性研究

(北京航天发射技术研究所, 北京 100076)

引言

提升机是一种变负载、多工况、机电液一体化的大型结构系统，其动态性能由于受多种因素影响，运动参数与负载不能用简单的数学模型描述，所以以往的设计方法主要以静态设计为主[1-2]。在液压提升机中直接影响整套设备性能的是液压系统的性能[3]。

为提高在大惯性负载运动控制系统中的控制精度同时减小冲击，尤其在军工等重要工业应用场合，国内外学者进行了多方面研究工作，在转载运输车起重系统中采用滑膜控制进行研究[4]； 通过对液压系统减震缓冲领域进行研究提高其负载适应性[5-6]；在提升机应用领域中为提高负载运行的稳定可靠性， 采用了模糊控制、反演鲁棒控制、复合控制等技术理论方法，取得了较高的控制精度[7-9]；在发射车跟踪控制领域采用非线性建模设计控制器探索研究[10]，但是由于其算法和计算量复杂性以及考虑到不同工业应用的成本，在实际工程中仍有许多问题亟待解决[8-9]。

本研究以某型号液压提升机为研究对象，通过对提升机液压系统进行建模仿真，分析系统特性，设计能够适应载荷及环境温度变化的控制器，进而通过试验的方法进行验证，为当前使用的液压提升机提供一种运行速度平稳的控制方法，保障系统工作过程中的稳定性和可靠性，同时为液压提升机设计提供理论依据。

1 数学建模

1.1 系统原理

某型号提升机液压系统原理图如图1所示。对提升机速率控制的液压放大元件采用的是比例流量多路阀，该阀的单路液压原理同电液比例阀，其性能介于开关阀与伺服阀之间，与电液伺服阀相比具有价廉、抗污染能力强等优点。除了在控制精度及快速性方面不如伺服阀外，其他方面的性能和控制水平与伺服阀相当，其动静态性能一般能满足大多数工业应用的需求。

提升机控制系统类型为电液比例速度控制系统，其控制结构由控制器、执行机构、被控对象和检测环节组成，其中执行机构包括液压动力源、比例多路阀、液压马达等元件，检测环节由拉线位移传感器组成，还有参与流程控制的油路压力传感器和载荷传感器等，控制系统组成框图如图2所示。

1.2 多路阀数学模型

多路阀单路流量调节原理与双向电液比例阀工作原理相同，其流量输出特性曲线如图3所示，本研究将以电液比例流量阀的原理进行建模分析。

由于电液比例阀电磁线圈频宽较液压系统频宽要宽的多，电流-电压模型可以等效为比例环节，其传递函数为：

(1)

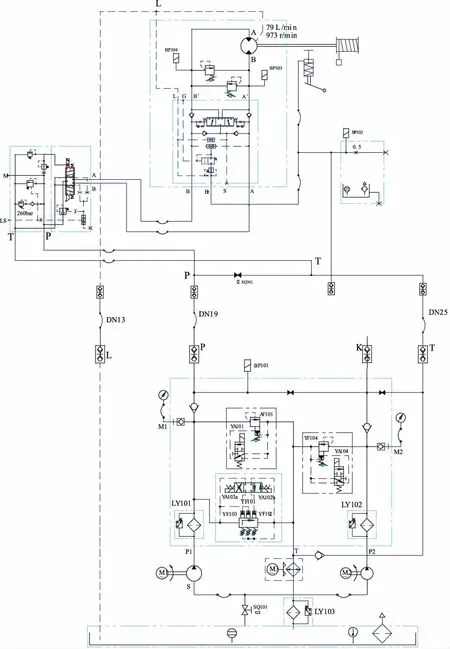
图1 提升机液压系统原理图

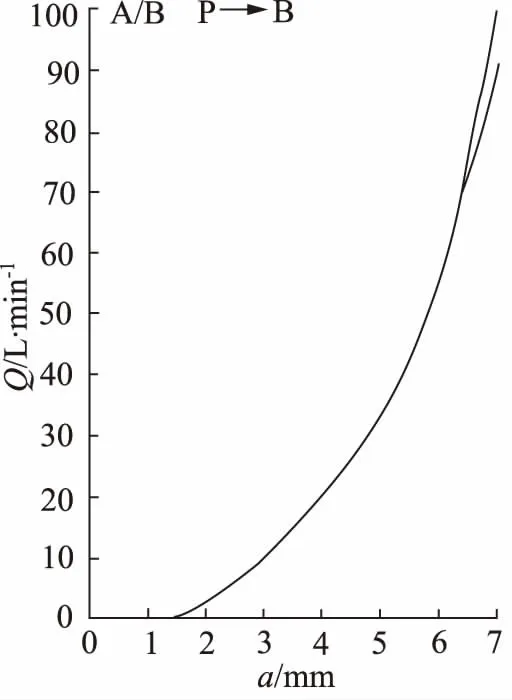
图3 多路阀流量特性曲线

图2 提升机控制系统结构框图

式中，Ie—— 额定工作电流

Ue—— 额定工作电压

电液比例阀阀开口位移-输入电流传递函数为：

(2)

式中，Ksv—— 阀的流量增益

ωsv—— 阀的自然角频率

ζsv—— 阀芯阻尼比

1.3 液压马达数学模型

由于比例阀与液压马达之间的油管连接距离很短，假定管道中的压力损失和管道动态可以忽略，液压马达每个工作腔内各处压力相等，体积弹性模量为常数，马达内、外泄漏均为层流流动[12]。

阀口流量方程：

qL=KqxV-KcΔpL

(3)

式中，qL—— 输出负载流量

Kq—— 流量增益系数

Kc—— 流量-压力系数

xV—— 阀开口位移

ΔpL—— 供油口与回油口压力差

马达流量连续性方程：

(4)

式中，Dm—— 马达排量

θm—— 马达转角

Cm—— 马达总泄漏系数，

Cl—— 内泄漏系数

Ce—— 外泄漏系数

Vt—— 马达总压缩容积

βe—— 有效体积弹性模量

马达负载力矩平衡方程，大负载力矩情况下系统主要以惯性负载为主，忽略摩擦负载、黏性负载和弹性负载：

(5)

式中，Jt—— 折算在马达轴向的总惯量

TL—— 作用在马达轴上的负载力矩

由式(3)～式(5)取拉氏变化计算得：

(6)

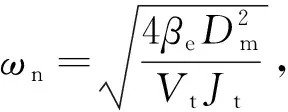
对式(6)取微分运算得马达角速度表达式:

(7)

从上式可以看出马达输出角速度与两个输入量有关，即为阀口开口位移大小和负载转矩大小，对于本研究的提升机系统，阀口位移作为控制输入量，负载力矩作为干扰输入量。角速度-阀口位移传递函数为：

(8)

角速度-负载力矩传递函数为：

(9)

传感器简化为比例环节可得阀控液压马达速度控制系统的结构框图，如图4所示。

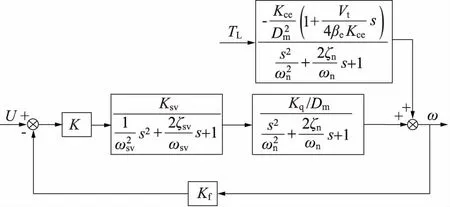
图4 阀控马达数学模型

2 系统仿真

2.1 时域分析

考虑到系统的非线性特性，在某一速度范围内做线性化处理，查阅比例阀和液压马达手册和实际测量计算，系统仿真用到的系统各参数如表1所示。

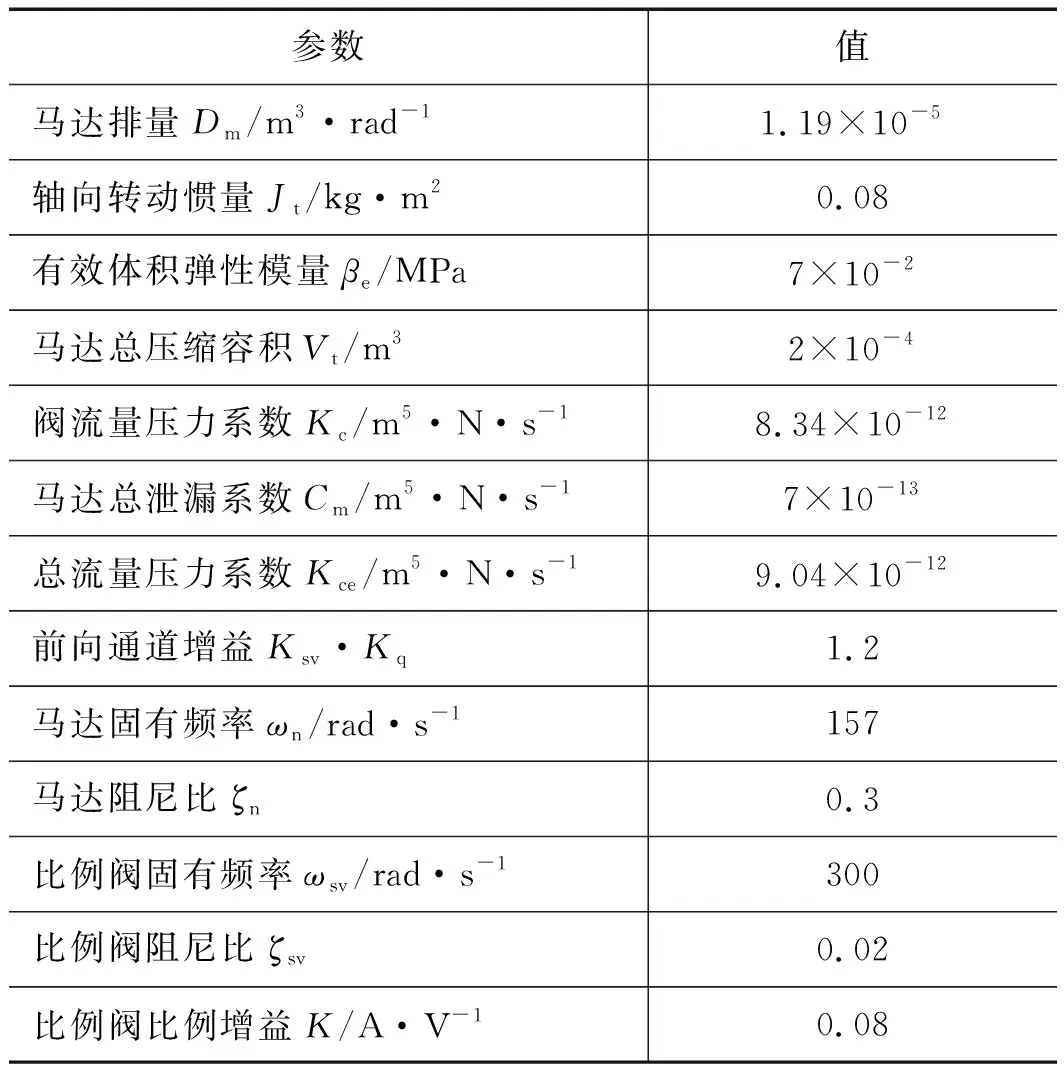
表1 系统仿真参数表

系统时域特性分析仿真结果如图5、图6所示，分别为阀芯位移阶跃响应输出曲线和系统角速度阶跃响应输出曲线，从图中可以看出系统阶跃响应呈震荡衰减特性。

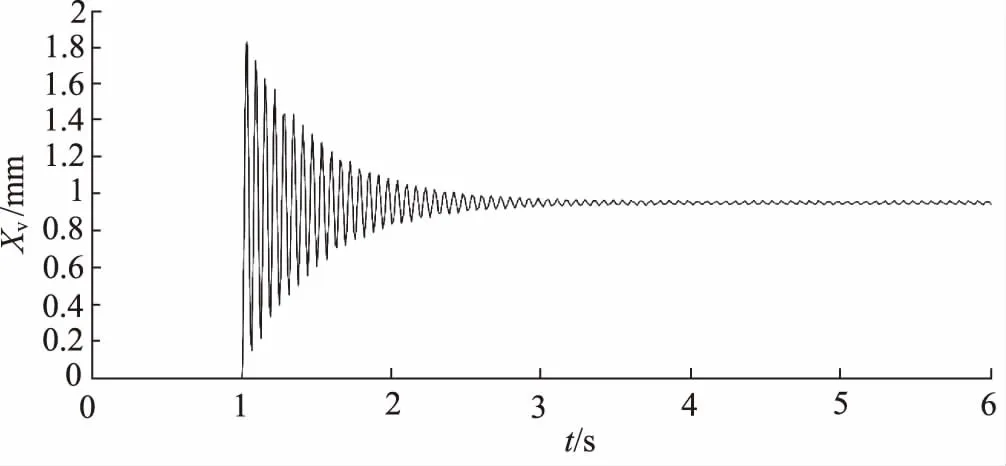
图5 阀芯位移单位阶跃响应输出曲线

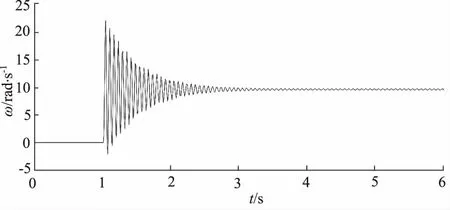
图6 马达角速度单位阶跃响应输出曲线

2.2 频域分析

提升机系统的动态响应特性是反应系统频响的重要特性，动态特性最能够分析出系统的灵敏度和跟踪特性，从系统的开环传递函数中可以看出没有不稳定极点，系统为最小相位系统，该提升机系统Bode图如图7所示。

图7 系统Bode图

从图7中可得，系统有谐振峰出现，谐振频率为12 Hz。相频在穿越180°时幅频特性大于0，系统不稳定。在设计提升机系统过程中应避免系统工作角速度在谐振频率附近，保证最高工作角频率(角速度)小于系统谐振频率。

3 控制策略

3.1 控制器设计

在系统带有负载情况下系统阶跃输入响应曲线如图8所示。

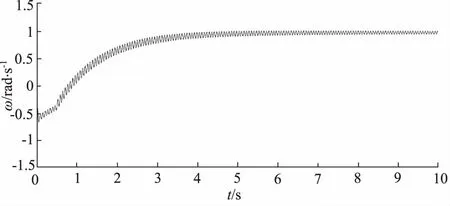
图8 PID控制器带载速度输出曲线

为了消除负载变化引起的速度偏差，提升机控制结构应用结构不变性原理引入前馈补偿控制器，从机理上消除负载引入的干扰输入，结构不变性控制结构原理图，如图9所示[13]。

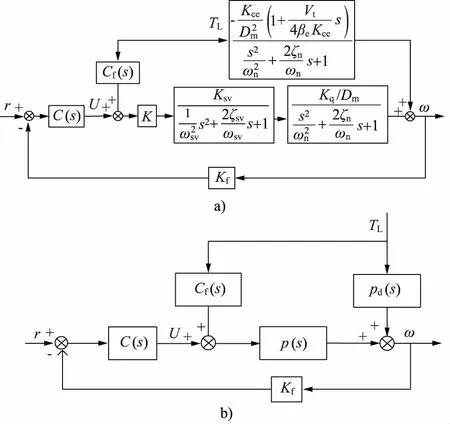
图9 结构不变性控制原理图

图9中前馈补偿控制器为：

(10)

图10中PID控制速度输出相应曲线为：

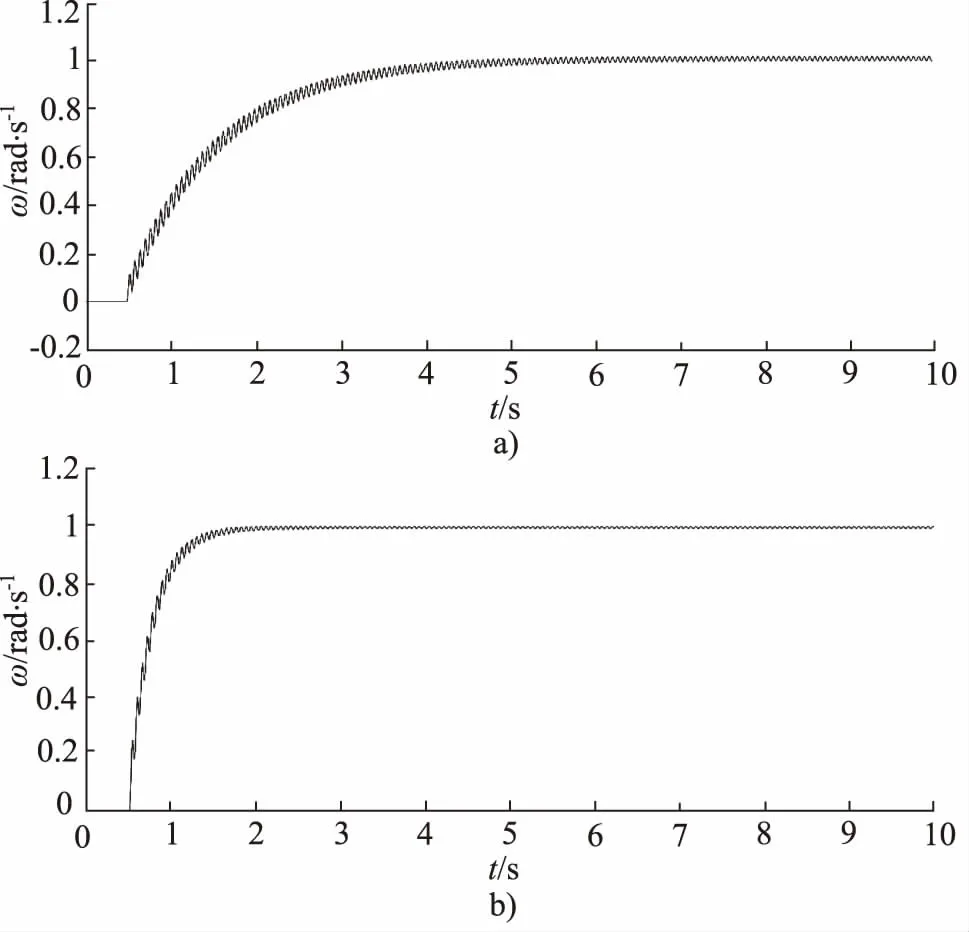
图10 不同控制器参数输出曲线

从图10a中PID 系数分别为0.2， 2， 0.0001；图10a中PID 系数分别为0.2, 20, 0.0001。可以看到，提高积分系数消除了系统静差，但是一味的增大积分系数会使得系统的I型主导极点作用加强，将会导致系统响应震荡发散。由于控制器实际输出有饱和阈值，不能设置太大的积分系数，在提升机控制系统中保证控制精度的前提下，通过调参设置合适的积分系数，并采用了积分饱和分离控制技术，控制效果良好。

从图11仿真曲线可以看出，系统在切换工作速度时进行恒加速速度规划时，提升机输出速度超调量小于1%，工作速度稳定可靠，这样保证了导弹装填的可靠性，有效减少了系统的动载荷、较小系统压力冲击，有利于设备的使用寿命和安全性。

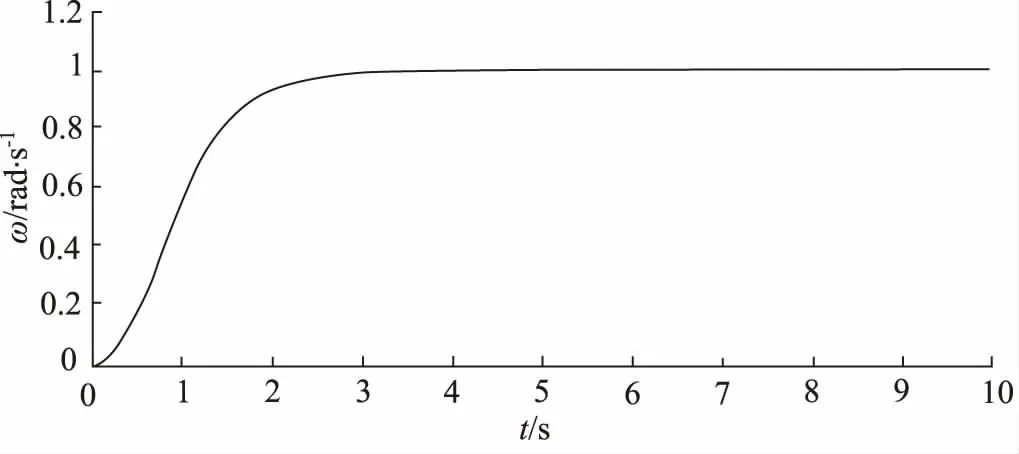
图11 速度规划仿真输出曲线

3.2 速度规划方法

由于比例阀流量特性的非线性引入可变步长输入，保证提升机在切换速度的过程中始终保持恒加速运动，有效控制系统的动载荷，设计方法如下：

确定非线性多路阀在恒加速运动时输入电压信号增量，获取比例阀多路阀流量-电压输出公式：

Q=ax2+bx+c

(11)

式中,a,b,c为常值系数。

获取速度-流量公式：

v=pQ

(12)

式中,p为常值系数。

式(11)代入式(12)得速度-电压公式：

v=apx2+bpx+cp

(13)

为使得速度在单位时间内均匀变化，将式(13)离散化处理，即：

v(k)=apx(k)2+bpx(k)+cp

(14)

从而得：

Δv(k)=v(k)-v(k-1)=

ap(x(k)+x(k-1))Δx(k)+bpΔx(k)

(15)

其中， Δx(k)=x(k)-x(k-1)

输入电压控制增量步长Δx(k)为：

(16)

恒加速运动即Δv(k)为常值，其输入信号步长为变步长，从而使得速度恒加速运行。

4 试验验证

经过以上对系统机理分析的结论以及控制算法的设计，最终试验的控制器选择计算能力和处理速度强大的DSP作为控制芯片[14-15]，分别给系统输入未加控制算法的阶跃信号和加控制算法的输入信号，分别对比系统响应输出曲线的相应速度和输出精度。

在相同20 t负载情况下加入适应负载变化的闭环控制器，并且在切换速度时进行输入速度规划，图12为流程速度输出曲线，从图中可以看出系统在速度切换过程中基本没有超调，切换平稳，只是在启动阶段由于阀存在输出死区，速度输出有超调，其阶跃响应与仿真结果图10、图11趋势一致。

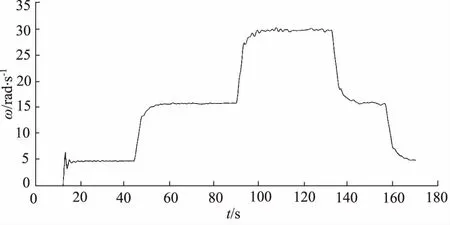
图12 20 t负载闭环控制速度输出曲线

图13为系统额定负载60 t情况下自适应控制速度输出曲线，控制效果与额定负载的25%，50%，75%负载情况下基本相同，系统工作稳定，速度切换平稳，超出速度控制精度5%范围内要求。

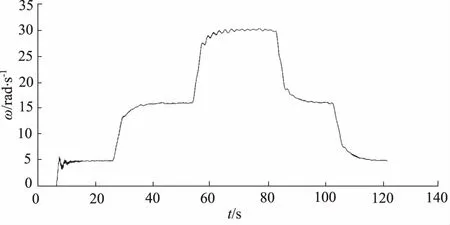
图13 60 t负载控制速度输出曲线

经过试验验证，本研究提的控制方法控制效果良好，能够满足使用和设计要求。

5 结论

在导弹提升机速度控制系统中，采用基于结构不变性原理和自适应变参数的闭环控制策略，能够满足不同负载情况下速度控制精度均在5%内的控制要求，在实际应用过程中将系统的动载荷保证在了0.1 t范围内在，减小系统压力冲击，能够保证导弹装填过程的安全性和可靠性。