改进PSO-RBF算法的锂电池额定容量实时估计

陈德海 马 原 潘韦驰

(江西理工大学电气工程与自动化学院 江西 赣州 341000)

0 引 言

锂离子电池作为一种可二次使用的供电能源，在民用、军事等领域被广泛使用[1]。实际使用中，锂电池容量会随着使用环境变化而有所改变，从而影响设备的性能，甚至引发严重的安全事故[2]。因此，准确估计锂电池在实际工况中的容量变化对研究电池健康状态(SOH)、荷电状态(SOC)[3-4]及预测其剩余使用寿命(RUL)有着至关重要的意义。

电池额定容量指的是在一定的放电条件(一定沉度、一定的电流密度和终止电压)，电池所能放出的最小电量。在实际工况下电池额定容量的预测会受到多种因素影响(环境温度、湿度等)，需要将其与电池健康状态(SOH)及剩余寿命(RUL)进行联合分析[5]。目前，电池额定容量预测的方法大致可分为3类：第一类，基于物理失效[6]的方法，依附于电池材料属性等建立模型。该方法无需大量数据，但此模型易受噪声和环境干扰，难以跟踪负载动态特性，动态精度较差。第二类，模型驱动[8]的预测方法。分析处理数据，依据图像或下降趋势，建立相对应的数学模型，该方法特征适应能力差，且依赖个人经验。第三类，数据驱动[7]法是对电池额定容量进行预测的主要方法。该方法是在统计学和数据挖掘等理论指导下，借助神经网络等机器学习算法，建立输入与输出变量间的关系模型。该方法具有一定的自适应性。但传统数据驱动模型的第一个弊端是，需要选取能显著反映模型特征的因素提高预测精度，如容量[9]、阻抗[10]等，但这类参数的获取较为困难，而能够直接测量的参数(电流、电压[11-12]等)维度较高，易受干扰产生误差。为此，文献[13]提出了一种基于核主成分分析(KPCA)法来提高预测精度，但该文献并未考虑偶发性因素(湿度、传感器灵敏度等)影响。传统驱动模型的第二个弊端是需要大量的数据支持，模型响应时间长，且数据量与训练模型的精度呈正相关。有学者利用现阶段应用最为广泛的粒子群(PSO)算法对BP神经网络[14]或者径向基神经网络(RBF)[15]进行优化。但单纯地使用粒子群算法进行优化，不仅会增加模型的复杂程度，还易陷入局部最优。若通过蚁群算法[16]及遗传算法[17]优化神经网络，算法的复杂程度高，且对开发平台硬件有一定要求。因此，本文针对现有方法自适应性差、数学建模复杂、未考虑偶发性因素影响等问题，引入一种改进的PSO-RBF模型，对电池额定容量进行快速、准确的预测。

1 动态额定容量标定模型

不同的工况环境、电池循环次数都会对电池的额定容量产生影响，多种因素的共同作用使得额定容量难以准确标定。因此，需要先将电池额定容量的影响因素按照影响程度划分为内部退化因素和特性影响因素。特性影响因素又可划分为主要影响因素(温度、放电倍率)和偶发性因素(传感器误差、湿度)。由内部退化因素和主要特性影响因素的动态、非线性特点，建立改进PSO-RBF算法预测模型，进行RUL预测，将预测结果输入至模型中结合特性因素进行额定容量预测，再根据实际应用场景，结合易于建立数学模型的偶发性因素对前者加以修正，最终实现对动态额定容量的快速准确预测。模型如图1所示。

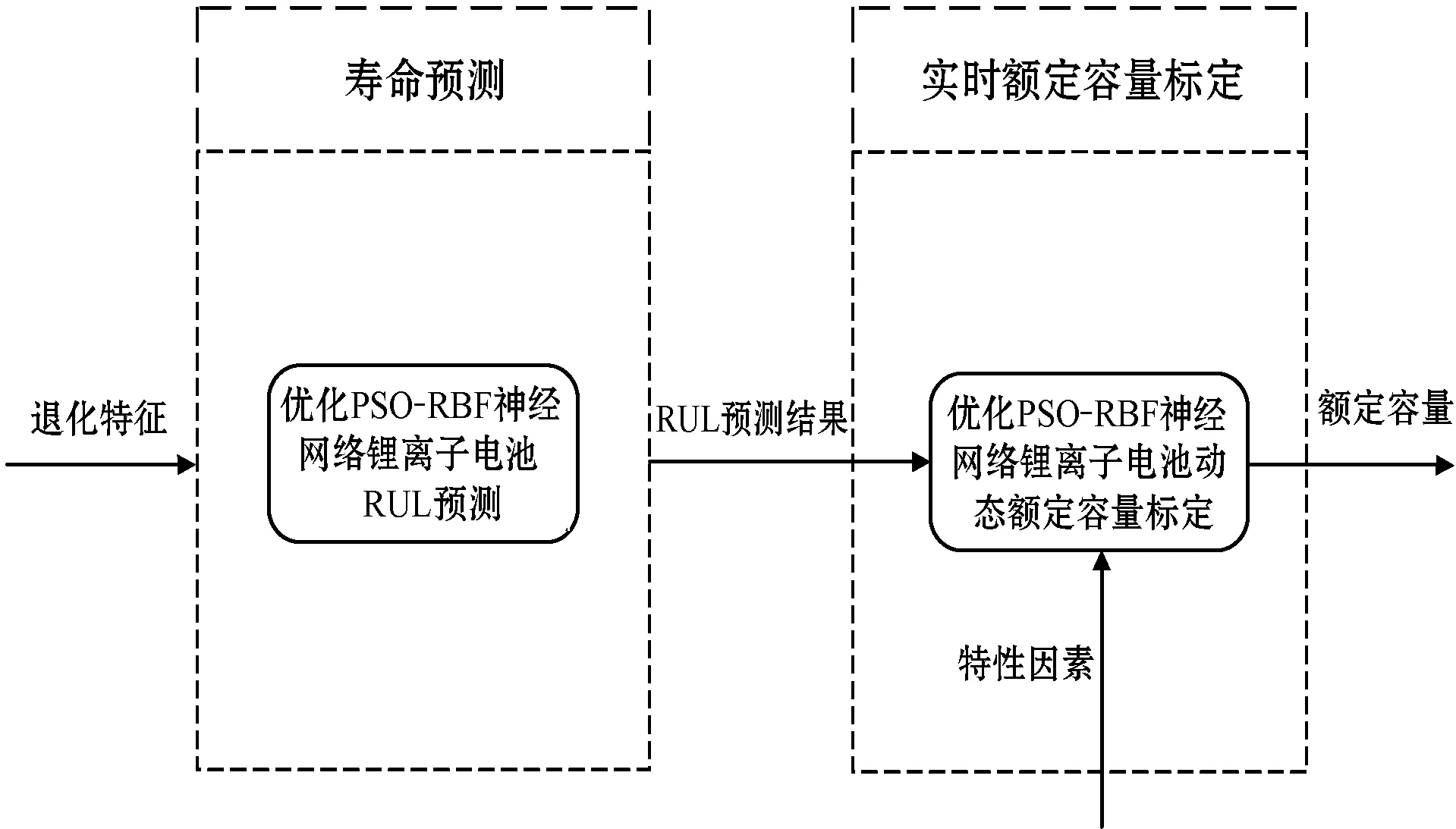
图1 锂电池动态额定容量标定

1.1 内部退化因素分析

电池在使用过程中，随着充放电循环次数的增加以及所处工况环境的变化，其内部化学平衡可能会遭到不可逆破坏。从而导致电池容量出现不可逆的容量退化[18]。因此，本文选取流、端电压等一系列直接可测的外部参数来表征电池退化程度，代入优化算法实现RUL预测。如图2所示，分别列举不同周期下的充放电电压随时间变化曲线。

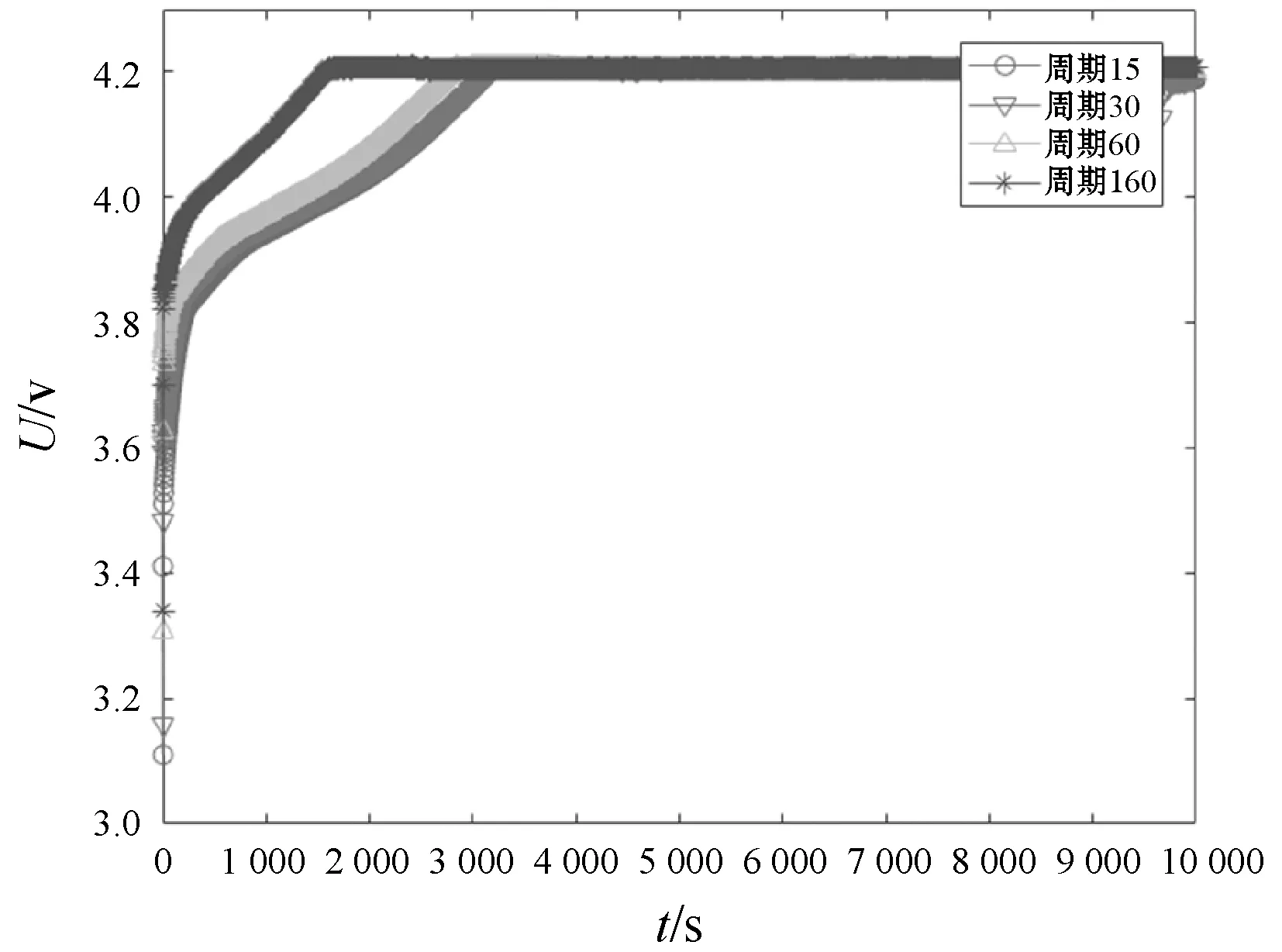
(a) 电池充电过程电压曲线

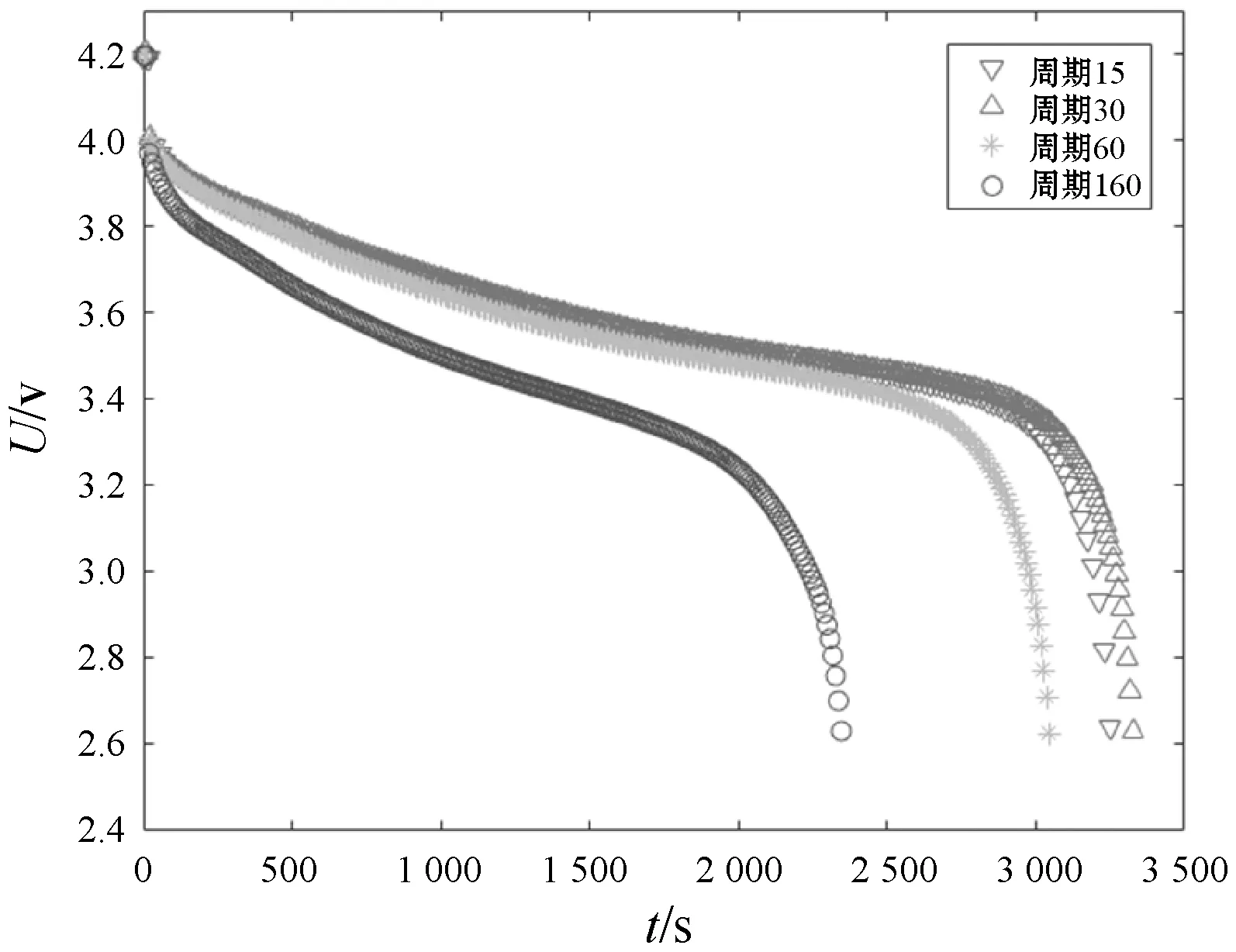
(b) 电池放电过程电压曲线图2 电池充放电电压曲线

1.2 特性影响因素分析

锂电池的标定容量定义为电池在25度环境下，以1C放电速率进行放电实验所能放出的电量。在实际工况下，连续两个充放电周期中，环境温度、电流充放电倍率的不断变化也会使电池的电容发生明显的改变，这些改变大都是可逆的[19]。若采用标准容量去替换动态额定容量进行分析必然会造成误差。因此，需要在预测RUL的基础上，将已经退化的电容结合此时的实际工况代入优化算法进行二次分析。

通过式(1)即可较为精准地对电池额定电容进行动态标定：

Cmin=anCold

(1)

式中：Cmin为额定容量，an为再生系数，Cold为经过退化后的电池容量。

1.3 偶发性影响因素分析

额定容量的偶发性影响因素如空气湿度、传感器灵敏度都会对额定容量的标定产生影响，此类因素具有偶发性，需要结合实际应用场景建立特定的修正模型。偶发性因素与特性影响因素存在一定的联系。在温度和放电倍率固定的情况下，偶发性因素会使再生系数的估算出现误差。因此，可以利用标准再生系数减小误差。

标准再生系数aN：在Arbin公司的测试系统下以25 ℃、1 C放电倍率进行放电测试得出的额定电容与自身的比值。每进行一次充放电循环更新一次末值。

(2)

式中：aN1,aN2,…,aNn为测试得到的标准再生系数。n表示次数，为了使aN具有自适应性，n的值设定为12。

通过标准再生系数即可计算得到由偶发性因素造成的误差ae为:

(3)

从而得到较为精准的额定容量式为：

Cmin=(aN-ae)Cold

(4)

2 算法优化

为了解决粒子群算法容易陷入局部最优解的问题，同时进一步提高神经网络的训练效率，本文提出了一种优化的粒子群算法将影响电池容量变化的内部退化因素和特性影响因素相结合利用径向基函数(RBF)神经网络训练模型，实现对于电池额定容量的预测。

2.1 标准RBF模型

在传统的BP神经网络的基础上建立的径向基神经网络(radial basis function，RBF)与BP网络相比具有结构简单、学习速度快、不存在局部极值等优点，在进行非线性数据的学习方面具有显著的优势。图3为径向基神经网络结构。

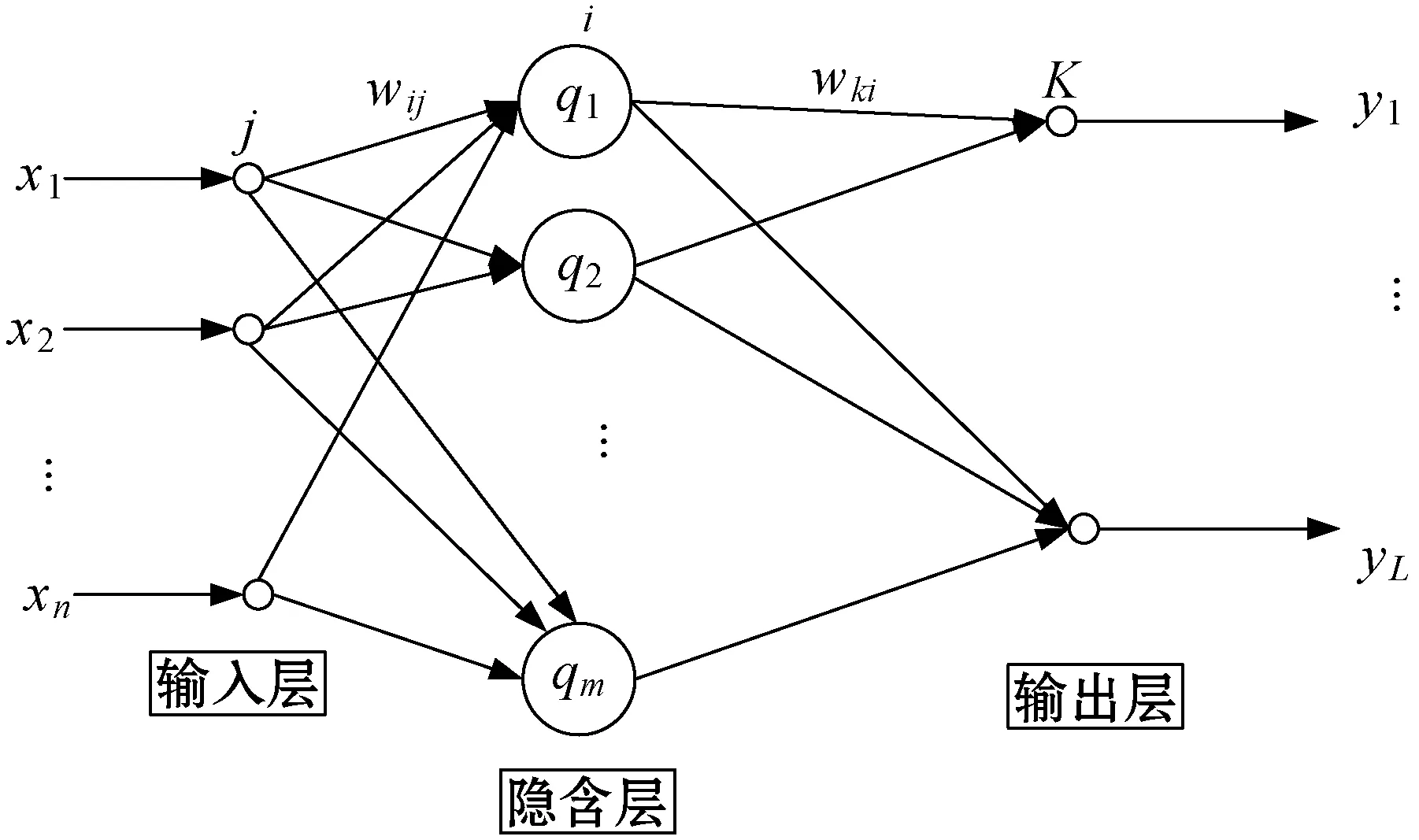
图3 径向基神经网络结构

图3中：x1，x2，…，xn为n维输入向量，q1，q2，…，qm为输入的m维向量，y1，y2，…，yL为输出的L维向量，隐含层到输出层的加权系数为wki，wij为输入层加权系数。隐含层的输出为：

(5)

式中:δi分别表示其对应隐节点的标准化常数;Ci表示为其对应的高斯函数的中心向量;XM为输入向量。输出层的输出为:

(6)

式中:wi为权系数。总误差为:

(7)

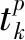
虽然RBF神经网络比BP网络处理非线性问题具有更好的自适应性，但影响其运行效果的三个参数q、Ci、δi无法确定,从而导致该算法具有很高的盲目性。

2.2 标准PSO

粒子群优化(particle swarm optimization，PSO)是通过种群间的相互竞争来寻找最佳觅食途径，从而快速寻找实际问题的最优解[20]。由于其具有模型简单、运算速度快等优势，被广泛应用。

在M维空间中，有N个随机移动的粒子。先定义粒子i的初始位置为xi=(xi1，xi2，…，xim)，并依次代入适应函数f(xi);设定粒子i的速度为vi=(vi1，vi2，…，vim);粒子i所经历过的最佳觅食点为pbesti=(pi1，pi2，…，pim);整个种群经历的最佳觅食点为gbest=(g1，g2，…，gm)。粒子i的第d维速度更新公式为:

(8)

粒子i的第d维位置更新公式:

(9)

由此可初步达到隐节点高斯函数的中心向量Ci和标准化函数δi：

(10)

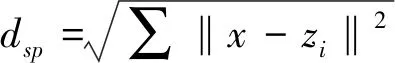
(11)

随着电池循环老化次数、实际工况的变化，电池容量具有非线性、时变的特性。PSO算法的性能受到多种参数影响，其中w、c1和c2对其搜寻性能和逼近能力有很大影响。始终使用同样的参数值进行模型训练，该模型可以拥有较快的运算速度但其精度相对较低且容易陷入局部极值造成误差。若根据实际需求不断改变参数值进行模型训练，后者的运算速度低于前者，但计算精度更高且具有一定的动态适应性，因此需要依据应用需求进行权衡[21]。为了避免陷入局部极值，同时提高自适应性及运算精度，设计了一种结合二者特性的参数组合优选模型，通过比较模型总体误差程度，对选取的参数组合进行优选，以满足应用需求。

2.3 改进的PSO

在粒子群的3个参数w、c1和c2中，可以先定义参数w的取值范围，其大致范围为：

(12)

式中：run为当前算法迭代次数;runmax为算法迭代总次数。先在定义的范围内选取一定的w固定值。前人试验表明当c1=c2=1.5时寻优效果较好，因此将其作为初值，其边界范围均为[0.5，2.5]，设置其步长为0.1。先改变参数w的值，c1、c2的值不发生改变，此时算作一组参数组合。同理，在新w值的基础上，在c1的对应范围内选值，c2不变，此时视为一组新的参数组合。以此类推，改变c2的值，如此w、c1、c2循环往复，在一定次数后，根据实验效果找寻其中使粒子群算法性能最佳的参数组合。然后由式(7)及PSO聚类算法得到RBF的参数组合q、Ci、δi作为最终训练结果。改进的PSO-RBF算法可以有效解决原有RBF法中参数q、Ci、δi难以确定的缺点。

3 实验测试

本文RUL预测实验数据来自于NASA PCOE研究中心提供的Battery Data Set。电池型号为18650型锂离子电池实验数据[22]。在NASA提供的实验数据中，当电容衰减量为30%时，实验停止。为验证预测方法的有效性，使用Battery Data Set中B5、B6、B7这3组数据重复实验。

3.1 RUL预测

第五组电池进行了168次循环放电，将奇数组数据作为训练样本，并用偶数组进行测试。同时引入KPCA的主元提取思想，将充放电过程中与电池容量退化显著相关的主元作为输入端，为了验证改进模型的预测性能，设计实验与经过主元提取的模糊神经网络(ANFIS)进行对比。拟合效果如表1所示。

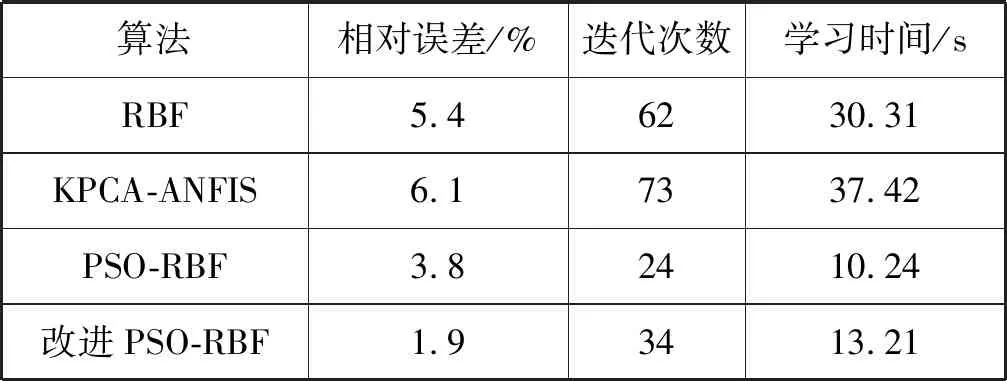
表1 三种方法对比

由表1可以看出，改进的PSO-RBF模型的学习时间与迭代次数均小于KPCA—ANFIS算法，且在几种算法中其相对误差最小。B5电池数据基于两种方法得到的RUL预测曲线和误差如图4所示，可以看出，改进后的算法预测曲线较为稳定且与真实值更加接近。优化后粒子群的参数为：w=0.259 7，c1=1.326 8,c2=2.432 0。

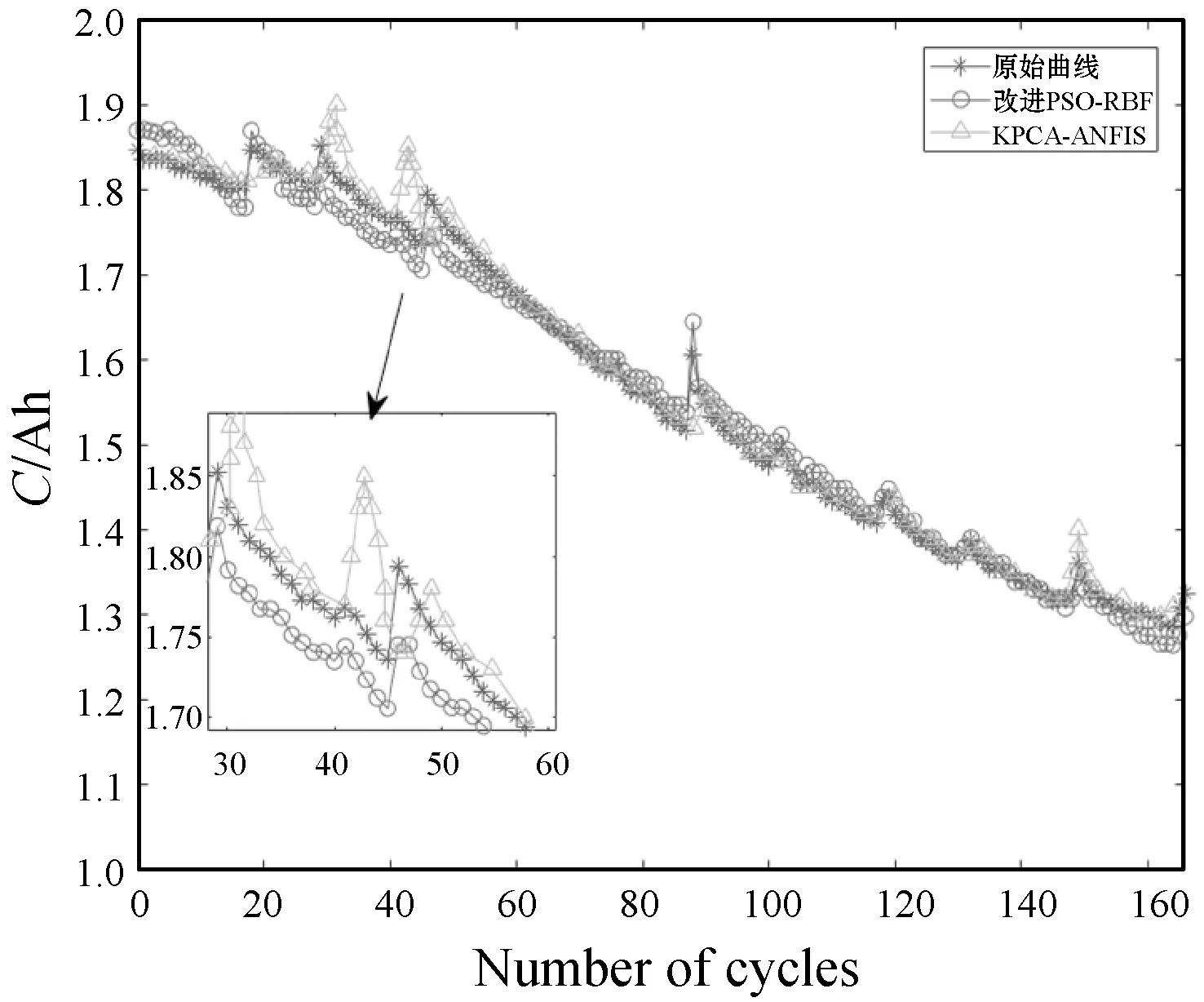
(a) RUL预测曲线

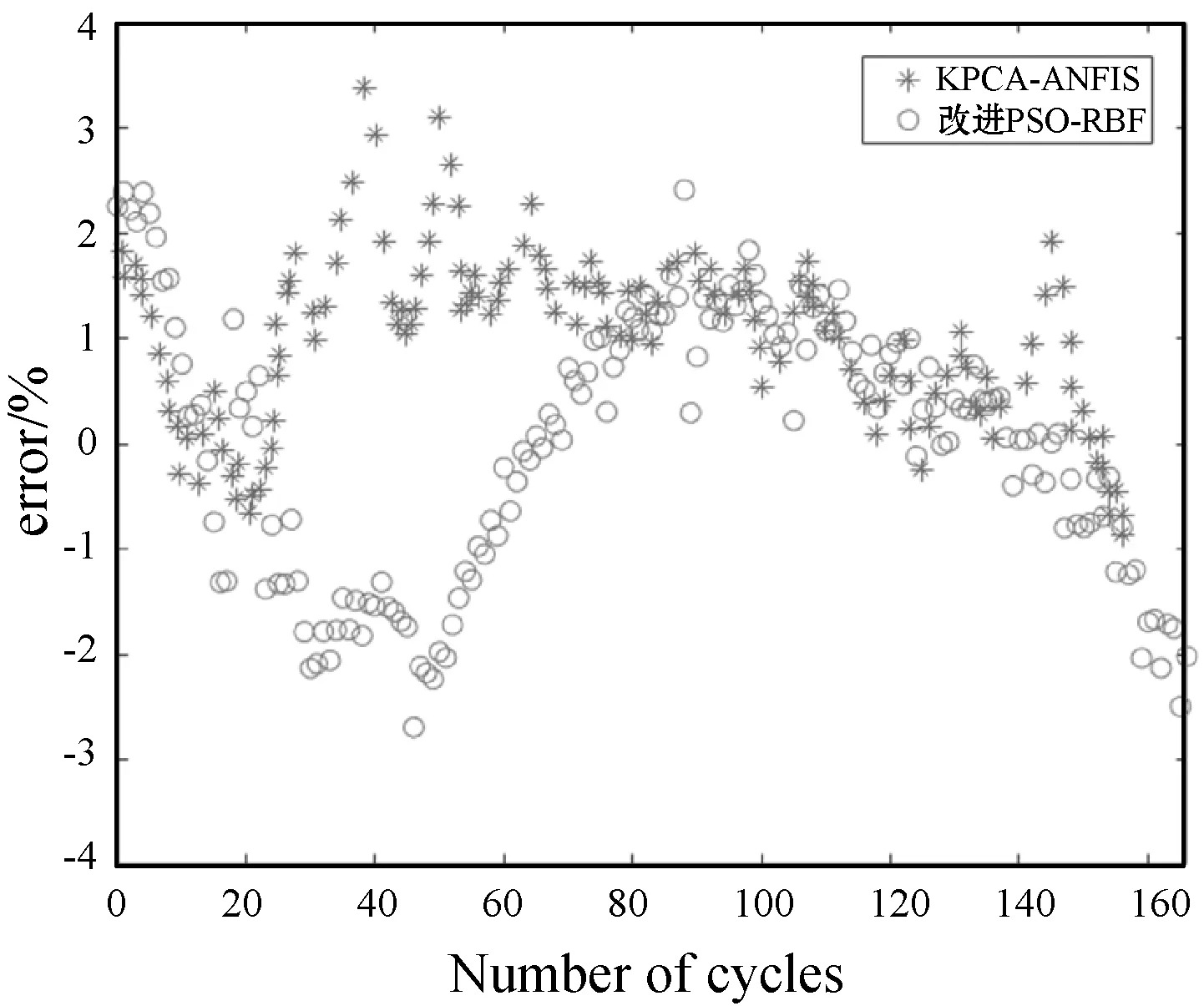
(b) 算法相对误差曲线图4 算法预测及误差曲线

为了进一步验证该算法的适用性，将优化后的粒子群参数代入，通过对比分析预测结果的均方误差(MSE)和平均绝对误差(MAE)值评测优化算法的性能。表2为由B6、B7组电池数据训练的改进模型与另外两种算法的预测效果对比结果。可以看到，优化后PSO-RBF的预测算法精度更高。

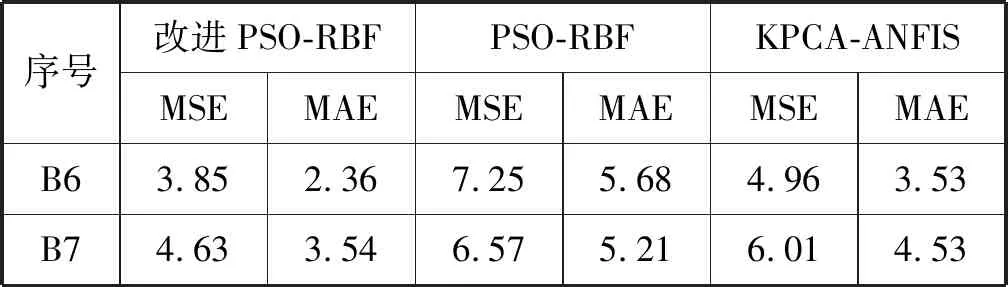
表2 电池RUL预测的网络MSE和MAE

3.2 动态额定容量标定

为了探究环境温度、电流充放电倍率对锂离子电池电容的影响程度，本文设计利用市面上的同型号18650锂电池进行实验。设计不同环境温度、充放电倍率下的实验。将几组电池在-20～25 ℃温度下分别以1/3～6 C的放电倍率进行充放电实验。为避免电池老化对实验的影响，实验以6个连续充放电周期为一组，每个周期间隔1小时。部分实验数据如表3所示。

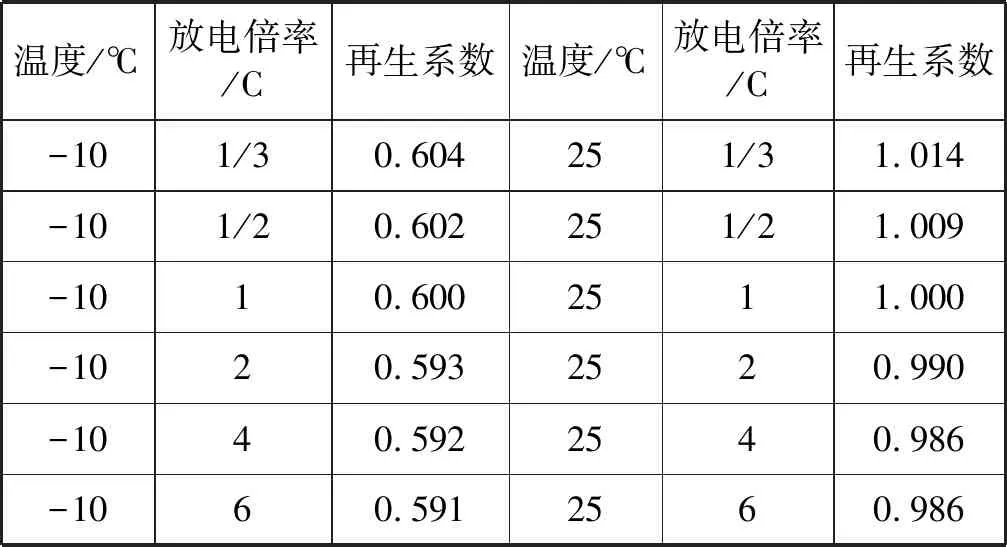
表3 不同情况下电容再生系数

由表可知锂离子电池的容量随温度升高而增大，相同倍率条件下，25 ℃的锂电池可放电容量比-10 ℃的增加了67%。

因此，实验设计第三组电池分别在不同温度不同放电倍率下进行实验。并将奇数组数据作为训练数据，偶数组数据作为预测数据。预测结果如图5所示。

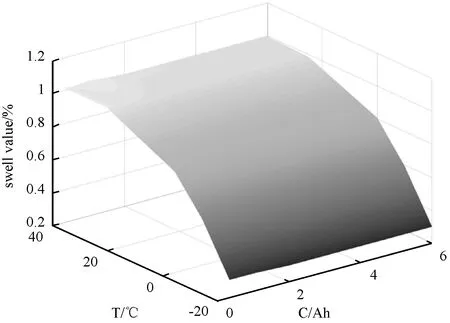
图5 容量再生预测曲线

最终由式(3)及实验数据得出的动态额定容量预测误差如图6所示，该算法可以较为准确地预测电池的实际额定容量变化曲线，平均误差为2.1%，在合理范围内。

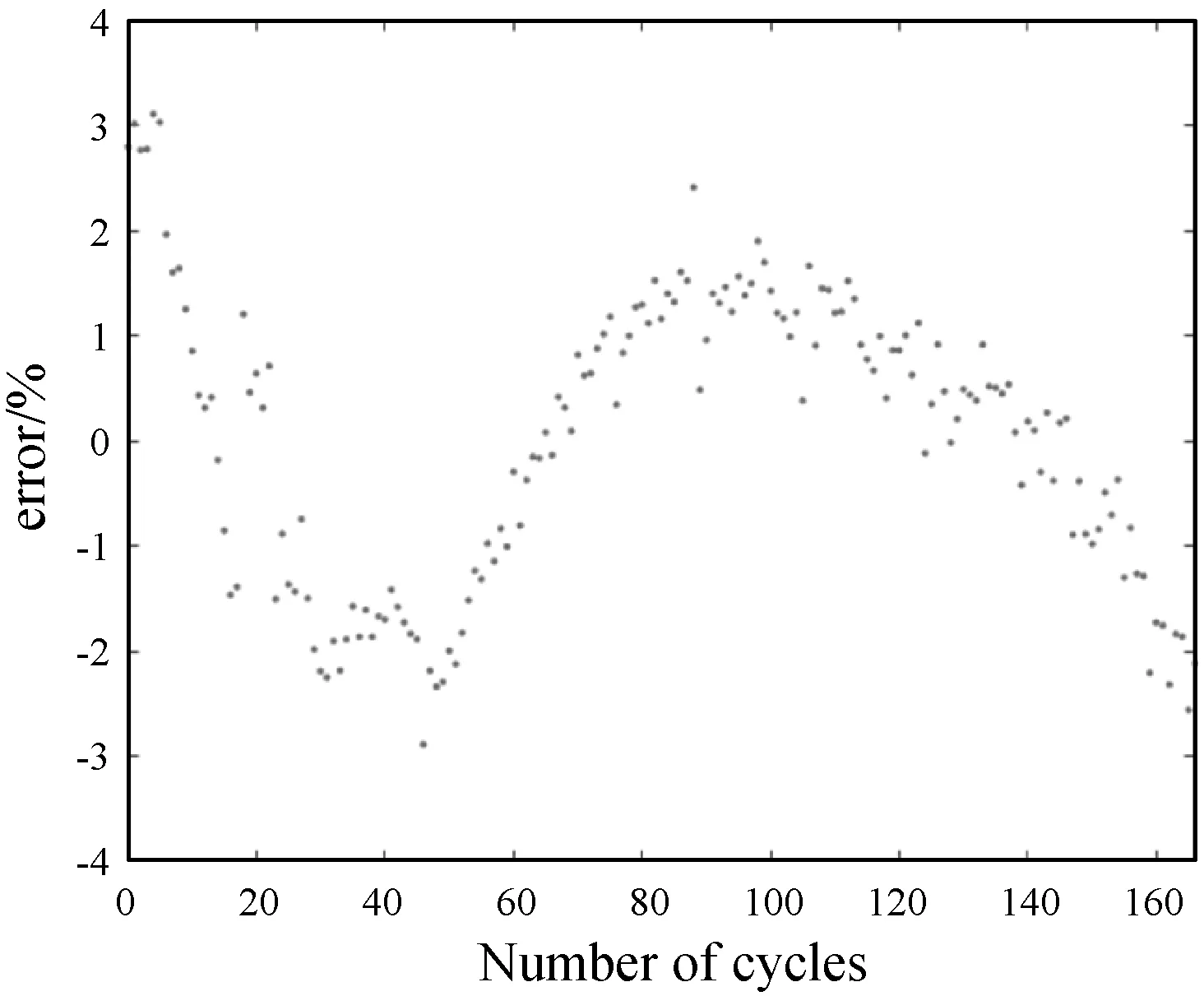
图6 容量预测误差曲线

4 结 语

本文根据电池额定容量受到多种因素影响的特性，将影响因素按照程度进行划分为退化因素和特性因素。由动态、非线性的影响因素建立改进PSO-RBF预测模型，再经由偶发性因素构建的应用场景模型对其进行修正，最终对锂离子电池的额定容量进行动态预测。实验结果表明该预测方法相比原方法响应速度明细提高。预测的平均误差为2.1%，验证了该算法具有一定可行性。