基于归一化Katz维数差的简支梁损伤定位研究

(榆林公路管理局 陕西 榆林 719000)

近年来，各种分形维数如盒维数、自相似维数、信息维数以及关联维数已经被广泛地运用于结构的损伤诊断中。同时越来越多的人将分形位数用于桥梁结构的损伤诊断当中。分形维数既可以对系统状态进行整体刻画，又不依赖于系统的数学模型，基于分形理论的桥梁结构损伤诊断使得判断结构损伤诊断较为容易。

一、Katz维数

文献[1]提出了一种估计波形的分形维数方法，也被叫做Katz维数[2][3][4]。Katz维数由于其对噪音的不敏感性常常被国内外研究人员所采用，曲线的分形维数(Fractal dimension)近似定义为：

(2.13)

其中d为曲线上第一个点与曲线内第i个点距离的最大值，可表示为d=maxdist(1,i)。L是曲线内线段总长度,n是滑动窗内的总样本数，定义为n=L/l。l为两相邻测点的平均距离(平均步长)。如图所示以(x3,y3)为中心，滑动窗含有4个样本距为例，求目标参数L,d。各参数已在图中梁段表示出来，以(x3,y3)为中心含4个样本距滑动窗L,d的计算公式为

(2.14)

(2.15)

图2-6 以(x3,y3)为中心含4个样本距滑动窗

显然，当滑动窗的样本距离数确定后，分形维数只与d/L的大小有关。Katz维数公式简单，计算方便快捷，对曲线的变化敏感，大量研究表明，Katz维数尤为适用于波动类曲线的计算。

L.J.Hadjileontiadisa等人提出的方法步骤为先在梁上建立一个滑动窗，窗内有若干个样本距离的滑动窗，使滑动窗沿梁的第一阶振型不断向后滑动，每次滑动的距离为一个样本距离，计算窗内的分形维数值，滑动了多少次便得到了多少个分形维数，通过结构上的分形维数分布进行分析，图像发生突变的地方就是结构可能产生损伤的位置，简称为FDCD方法。

本文利用归一化损伤前后的Katz维数差进行简支梁的损伤定位。

线性归一化可设振动振型的竖向位移为y，振型中最大最小竖向位移分别是ymax和ymin归一化后振型数据为y*，振型归一化的方法如式：

二、有限元模型及损伤定位

采用长a=2m,宽b=0.24m,高c=0.05m，密度、弹性模量和泊松比分别为8000kg/m3，200GPa，0.25的简支梁模型进行归一化Katz维数差的损伤诊断有限元分析，利用刚度的折减来模拟损伤。如图

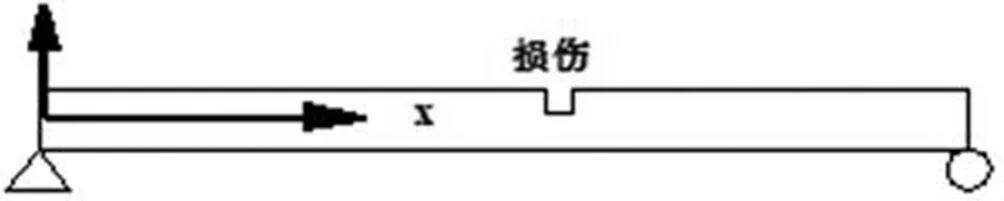
图1 存在损伤的简支梁

分析时将全梁分为200个梁单元，每个单元长1cm。首先选定样本距离为dx，并建立包含n(偶数)个样本距离的滑动窗，n为偶数的原因是可以使滑动窗内的Katz维数落在其样本点上，取n=2,样本距离dx分别取1,5,8cm。损伤工况在x=0.2～0.25m处发生损伤，刚度变为原来的0.8。绘制损伤后分形维数图2(a)(b)(c)。

(a)dx=1cm (b)dx=5cm (c)dx=8cm

从图中可以看出，Katz维数差均在损伤处达到了最大值，说明用Katz维数差取定位损伤是有可行性的，同时，样本距离相对较小的归一化Katz维数差对损伤的识别越明显。

通过建模基于归一化Katz维数差对简支梁的损伤定位，可以得出以下结论:

1.利用归一化Katz维数差可以在选定的样本距离和样本数下，对简支梁单损伤进行定位。

2.在采样数n确定的情况下，采样距离较短时对损伤更加敏感。