考虑交通信息与配电网结构的充电站规划

洪彬倬，冯乙峰，阳细斌，武小梅，许方园

(1.广东电网有限责任公司阳江供电局，广东 阳江 529500；2.广东工业大学 自动化学院，广东 广州 510006)

作为智能电网的重要组成部分，电动汽车产业已经发展成为国家的战略性新兴产业。电动汽车充电站作为电动汽车充电的重要基础设施，需要提前完成合理的规划布局，实现与电动汽车的协调发展；因此，对电动汽车充电站的规划研究具有重要意义。目前，国内外学者在充电站的选址定容方面虽然做了一些研究[1-5]，但是还没有形成成熟的理论。文献[6]采用K-means算法来进行充电站选址和服务范围划分；文献[7]考虑了碳排放因素，采用Voronoi图来获得充电站服务范围，从而得出充电站规划方案。虽然上述研究在充电站规划中考虑了诸多因素，但这些文献在充电需求点到充电站的距离计算上采用欧氏距离乘以非直线系数的方法，并未考虑电动汽车的实际行驶路径，规划结果不够合理。文献[8]采用Voronoi图和改进粒子群算法进行充电站规划；文献[9]预测电动汽车的充电需求量，通过Voronoi图最小化用户在充电站途中的成本，从而得出充电站规划方案；文献[10]分析了用户的充电行为，提出多目标规划模型；文献[11]以电动汽车用户群体空驶成本最小化为目标进行充电站选址规划，以周最大充电负荷来确定充电站容量；文献[12]综合考虑充电站方和用户方的利益，通过萤火虫算法求解模型。虽然上述研究均构建了合理的充电站规划模型，但这些文献并未考虑充电站规划对配电网的影响，充电站负荷过大可能导致配电网出现部分节点电压越限、线路传输功率达到上限等不利情况。文献[13]考虑多方利益，结合Voronoi图和Floyd算法来划分充电站服务范围，采用优化算法对模型进行求解；但文中在得到充电站的位置后没有进一步考虑充电站的配电网接入，且文中以交通节点作为候选站址，考虑得不够全面。

针对上述问题，本文充分考虑电动汽车充电站投资方、电动汽车用户和配电网运营方的利益，以充电站建设成本、运维成本、用户出行成本和配电网网损成本之和最小作为规划目标，采用基于Floyd距离的Voronoi图思想来确定交通节点所属服务区，在规划中考虑了实际路径的问题，建立充电站的选址定容模型，并通过改进的粒子群算法进行求解，得到充电站选址定容方案及配电网节点接入方案。

1 充电站选址定容模型

1.1 目标函数

充电站的规划原则是在满足规划区域的路网和配电网的相关约束的前提下，在多组可行方案中选择成本最低的方案。选择充电站建设成本、运维成本、用户出行成本和配电网网损成本之和作为社会总成本C，即

(1)

式中：N为充电站个数；C1i为充电站i的年建设成本；C2i为充电站i的年运维成本；C3i为充电站i服务范围内的电动汽车用户的年出行成本；C4为接入充电站后配电网增加的年网损成本。

a)充电站的年建设成本。充电站i的年建设成本

(2)

式中：mi为充电站i的充电桩数量；F为充电桩单价；ei为充电站i的变压器数量；E为变压器单价；li为充电站i到其接入的配电网节点的中低压线路长度；cl为线路单位成本；ωi为充电站i的基建费用；r0为贴现率；a为充电站的运行年限。

b)充电站的年运维成本。充电站的年运维成本研究较为复杂，文章将充电站i的年运维成本C2i简化为年建设成本乘以比例系数η，即

C2i=(miF+eiE+licl+ωi)η.

(3)

c)电动汽车用户年出行成本。有充电需求的电动汽车用户在前往充电站充电的路途中消耗了电动汽车的电能且浪费了自己的时间，充电站i服务范围内的电动汽车用户的年出行成本

(4)

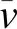
d)接入充电站后配电网增加的年网损成本。充电站接入配电网之后会造成配电网的有功网损增大，其增加的年网损成本

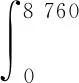
(5)

式中：p为电网公司含税网购平均电价；Ploss1为未接入充电站之前配电网的有功网损功率；Ploss2为接入充电站之后配电网的有功网损功率；t为时段。

1.2 定容方法

充电站的容量配置应满足其服务范围内的电动汽车的充电需求，且所有充电站的服务范围应涵盖规划区的所有路口节点。定义充电站服务范围内的充电需求为[14]

(6)

式中：Wi为充电站i的典型日充电需求量；ni为充电站i服务范围内的交通路口数量；qk,t为路口k在t时段内流入的车流量；α为电动汽车所占比例；β为有充电需求的电动汽车比例；Wev为电动汽车电池的平均充电容量。

充电站的容量配置由其服务范围内的充电需求决定，则充电站的充电桩数量配置为

(7)

式中：μ为充电站的充电容量裕度；P为充电桩的充电功率；Tt为充电桩的日充电有效时间；kt为充电桩的工作同时率；keff为充电桩的充电效率。

1.3 约束条件

充电站在规划过程中需要满足路网和配电网的相关约束，否则会出现交通阻塞、配电网节点电压越限等情况[15-17]，主要约束条件如下：

a)充电站内充电桩数量约束。由于充电站建设过程中受到地形和接入配电网节点容量等因素的限制，其容量应在一定范围内，即

mi∈[mmin,mmax].

(8)

式中：mmin为单个充电站的充电桩最小数量限制；mmax为单个充电站的充电桩最大数量限制。

b)充电站数量约束。充电站数量由规划区内充电需求和充电站容量限制决定，如下式所示：

(9)

(10)

式中：Smin为单个充电站的充电桩最小容量限制；Smax为单个充电站的充电桩最大容量限制；Nmin为规划区充电站的数量最小值；Nmax为规划区充电站的数量最大值；W为规划区电动汽车的总充电需求。

c)配电网节点电压约束为

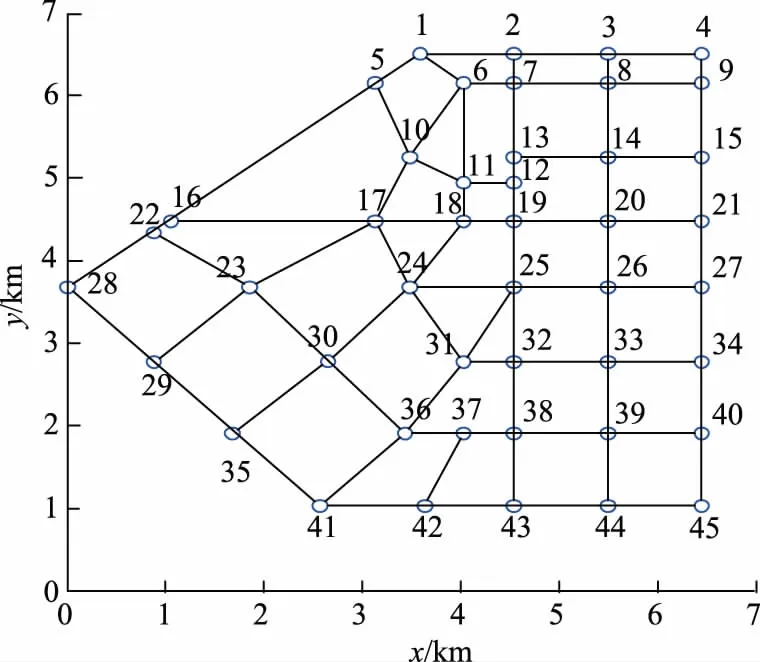
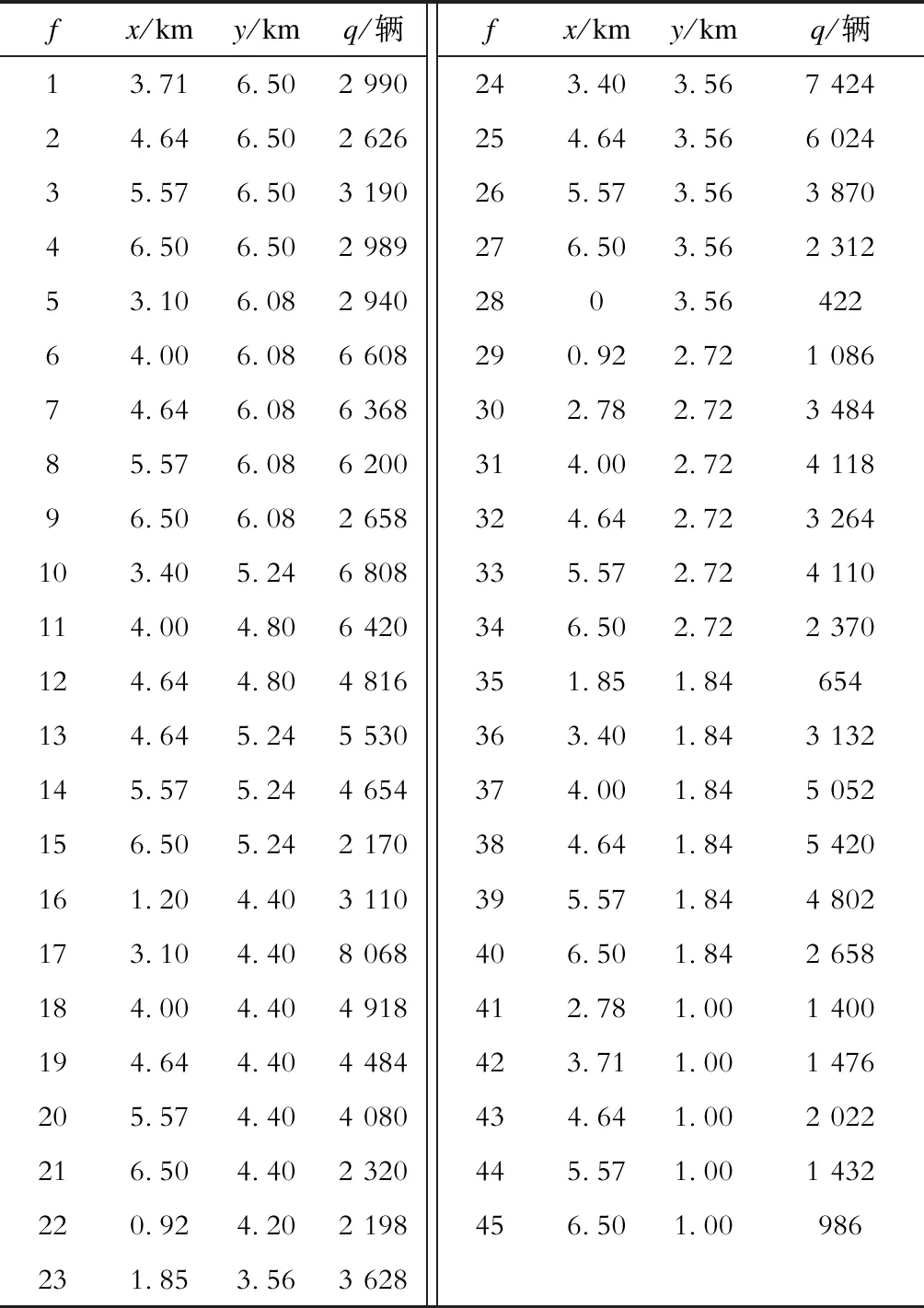
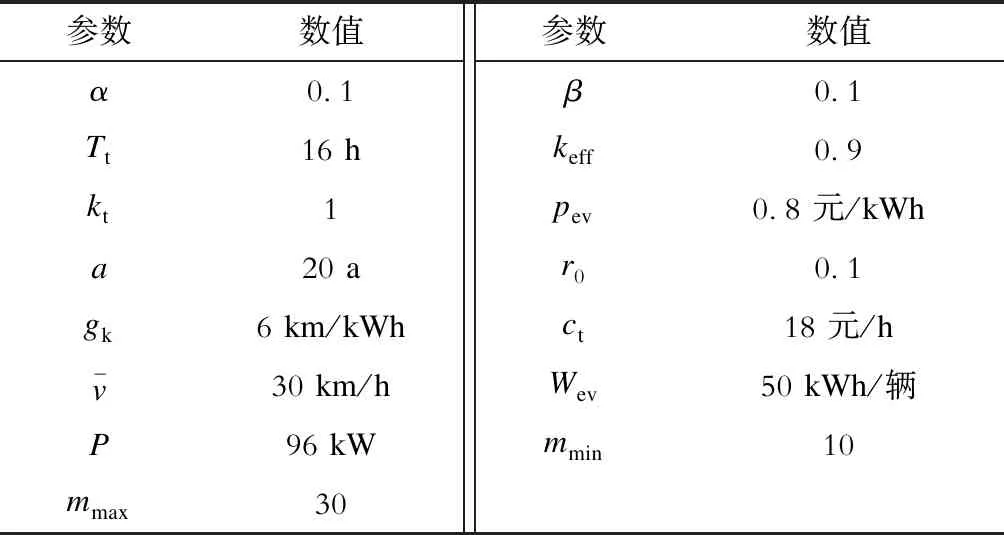
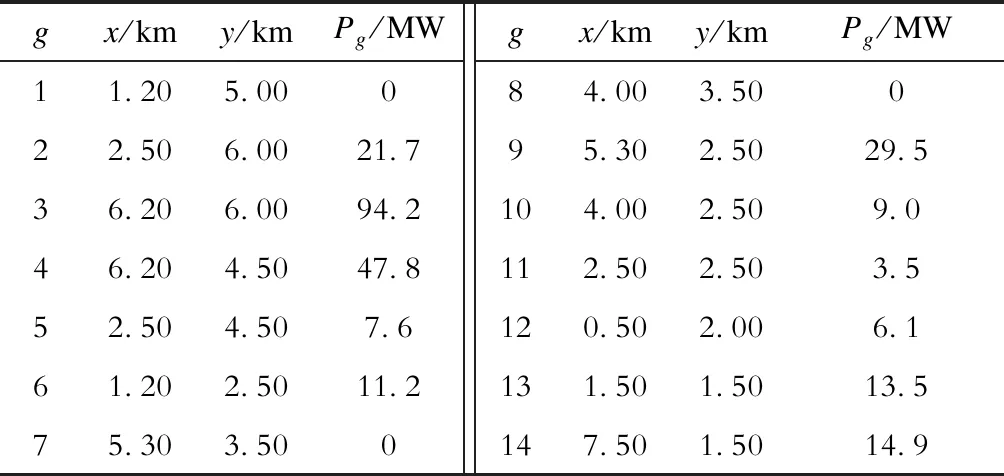
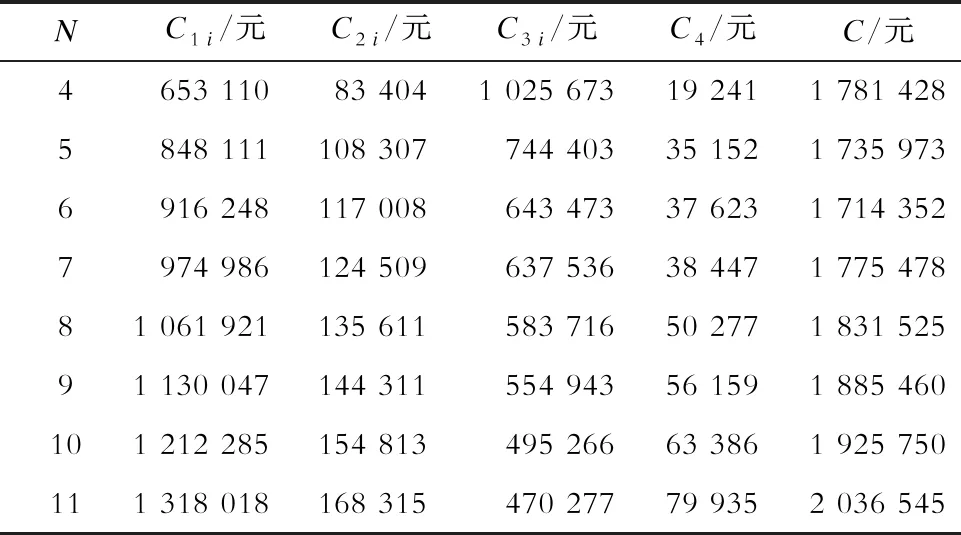
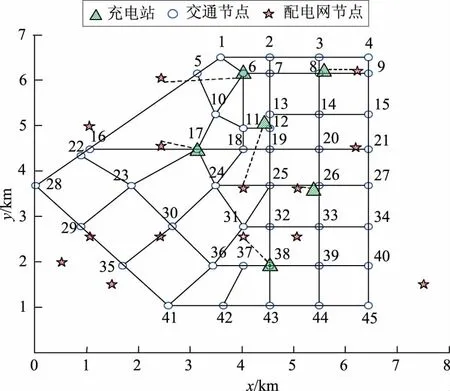
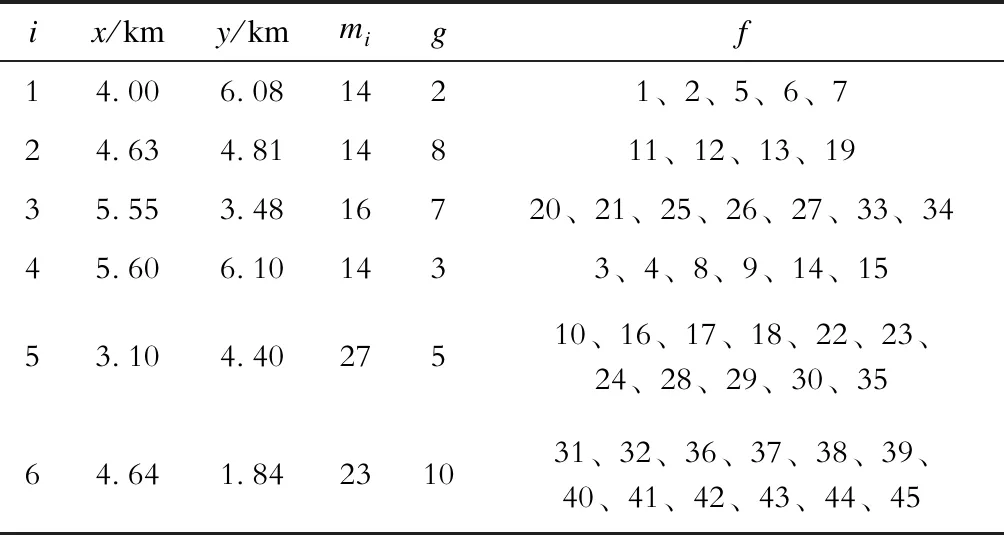
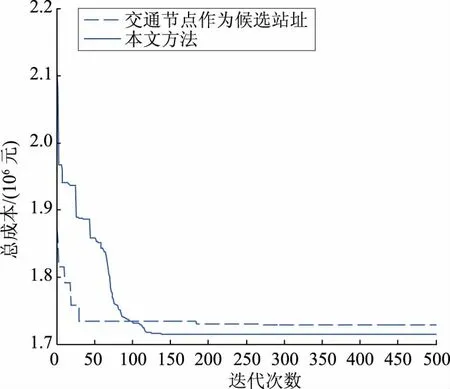
Ug,min

(11)

式中：Ug为配电网节点g的电压幅值；Ug,min、Ug,max分别为配电网节点g的电压幅值下限、上限；M为配电网节点的数量。

d)充电站接入的配电网节点容量约束为

Pi,g+Pg≤Pg,max.

(12)

式中：Pi,g为充电站i接入配电网节点g的充电功率；Pg为节点g的负荷功率；Pg,max为节点g允许接入的最大功率。

e)配电网潮流等式约束为

(13)

式中：Pg和Qg分别为配电网节点g处的有功功率和无功功率；Uh为节点h的电压幅值；Ggh和Bgh分别为支路gh的电导和电纳；θgh为节点g、h之间的相角差。

1.4 充电服务区划分

电动汽车用户在有充电需求的时候倾向于到最近的充电站充电，因此交通节点到充电站的距离是划分充电服务区的重要依据。

Floyd算法是利用动态规划思想在两点之间的多条路径中寻找最短路径的算法[18-20]；而Voronoi图是在平面中分别计算所有点到不同中心点的欧氏距离，按照最邻近原则来划分交通节点的归属，从而划分服务区[21-26]。在充电站规划中，不同地点之间的距离若采用欧氏距离公式或者欧氏距离乘以道路曲折系数的方式来计算显得不够准确，在这里拟在Voronoi图中采用Floyd距离代替欧氏距离来进行充电服务区划分，数学表达式为：

V(i)={f∈V(i)|dture(f,i)

(14)

dture(f,i)=dfloyd(f,r)+deuc(r,i).

(15)

式中：V(i)为充电站i的Voronoi服务范围，i=1,2,3,...,N和j=1,2,3,...,N且i≠j；r为离充电站i最近的交通节点；dfloyd(f,r)为交通节点f和r之间的Floyd最短距离；deuc(r,i)为交通节点r和充电站i之间的欧氏距离；dture(f,i)为交通节点f到充电站i的真实距离。

2 规划过程

本文采用的规划策略是：首先根据充电站的容量限制[Smin，Smax]来确定充电站的数量范围[Nmin，Nmax]，从N=Nmin开始产生N个初始站址，通过基于Floyd最短路径的Voronoi图来计算交通节点到各个充电站的真实距离并进行充电站服务范围划分，进而计算各项成本，寻找其最优的充电站站址和容量。在配电网容量和潮流约束条件下，反复计算，调整分区的服务范围和充电站站址，得到N所对应的电动汽车充电站规划的最优方案。令N=N+1继续迭代，直到N=Nmax。最后得到不同N对应的最优成本并选取总成本最低的规划方案作为最终规划方案，具体流程如图1所示。

3 算例分析

以文献[13]中的典型规划新区的交通网数据为例，该新区交通网有45个主要路口节点，78条道路，如图2所示，图中节点处的数字为该节点编号，x为节点横坐标，y为节点纵坐标，各交通节点的坐标及对应的典型日车流量q见表1。本文借鉴文献[27]中的参数设置，合理假设电动汽车充电站的相关参数，见表2。规划区配电网结构采用IEEE 14节点模型，配电网节点位置及其对应容量见表3。

由式(9)、(10)可得到充电站数量N的取值范围为[4，11]，分别对每个N进行迭代计算；对于每一个确定的N值，随机产生N个初始站址后，结合交通节点的坐标信息和式(14)、(15)可得到各个交通节点之间的floyd最短距离和对应的充电站归属划分；通过交通节点的车流量信息和式(6)、(7)可求得各充电站的充电桩数量(即充电站容量)；然后结合各充电站的容量和交通节点间的floyd距离等数据，采用式(1)—(5)可得到充电站各项成本和总成本；通过算法不断迭代更新站址，比较总成本从而得出充电站最优规划方案。每个N值对应的最优成本如图3和表4所示。

图1 充电站规划流程Fig.1 Charging station planning flow chart

图2 规划区道路网Fig.2 Planning area road network

表1 交通网节点坐标及其车流量Tab.1 Traffic network node coordinates and traffic flow

表2 充电站基本参数设置Tab.2 Basic parameters setting of charging station

表3 配电网节点位置及负荷Tab.3 Distribution network node location and load

图3 总成本与充电站数量和迭代次数的关系Fig.3 Relationships between total cost and numbers of charging stations and iterations

表4 不同充电站数量对应的成本Tab.4 Cost corresponding to the number of different charging stations

充电站的建设和运维成本与充电站数量和充电桩数量等因素有关，充电站的数量越多，充电站内的充电桩数量越多(即容量越大)，则建设和运维成本越大；用户的出行成本与用户到充电站充电的行驶距离有关，充电站数量越多，则用户出行成本越小。由图3和表4可知，当随着充电站数量不断增多，充电站建设成本和运维成本不断增大，而电动汽车用户的出行成本不断降低。当充电站数量为6的时候，充电站总成本达到最低；因此本文针对充电站数量为6的情况展开分析，以充电站年建设成本、年运维成本、用户出行成本和配电网网损成本之和最低为目标，采用基于Floyd距离的Voronoi思想划分充电站服务范围，通过改进优化算法求解得到充电站规划方案。其中充电站的站址分布和与配电网节点的连接方式如图4所示，充电站的站址、容量、交通节点和配电网连接节点见表3。

图4 充电站布局及接入的配电网节点Fig.4 Charging station layout and access network nodes

表5 充电站规划结果Tab.5 Charging station planning results

为了验证本文方法的充电站规划优化能力，以本文采用的交通网数据及相关参数为例，当充电站数量范围在[4，11]的情况下，分别采用以交通节点作为候选站址的方法和本文方法对算例进行仿真计算，得到不同充电站数量下2种方法中最优方案对应的总成本(如图5所示)，充电站数为6时的迭代过程如图6所示。由仿真结果可得，2种方法均在充电站数为6的时候达到最优，本文方法的总成本为171.4万 元，候选站址方法对应的总成本为172.7万 元，本文方法结果占优，且本文方法在规划过程中未把充电站选址限制在交通节点，并在得到充电站的位置和容量后进一步考虑充电站的配电网接入，使得规划结果更加合理、全面。

图5 2种方法规划结果对比Fig.5 Comparison of planning results of two methods

图6 充电站数为6时的总成本迭代曲线对比Fig.6 Comparison of total cost iteration curves with 6 charging stations

4 结束语

大规模推广电动汽车需要对充电站进行合理的规划，不合理的充电站选址定容规划会导致充电效率低下、交通堵塞和配电网容量越限等情况的出现。本文综合考虑充电站建设方、电动汽车用户和配电网运营方等多方利益，在规划中考虑了路网结构中的真实路径，采用Floyd算法、Voronoi思想相结合的方法来建立充电站选址定容模型，具有一定的现实意义。算例结果表明，采用的方法可以得到合理的电动汽车充电站选址定容方案及配电网节点接入方案。

但在现实规划中，本研究中的方法仍存在一些潜在问题以及不足之处，例如本研究中的部分模型参数(电动汽车充电同时率、充电桩充电效率等)为参考其他文献后假设得到[28]，但在实际规划中这些参数的取值仍需商榷；另外本研究中并未考虑电动汽车车主的充电偏好、充电站中快慢桩的配置比例以及不同区域的土地性质等问题。在下一阶段本文拟针对上述问题做进一步的规划研究，得到更加合理的充电站规划方案。