基于自适应动态规划的售电商长期收益研究
冯小峰,谢添阔,文宏武,白恺
(1.广东电网有限责任公司计量中心,广东 广州 518049;2.华北电力大学 电力工程系,河北 保定071003;3.广东电网有限责任公司湛江供电局,广东 湛江 524000;4.广东电网有限责任公司韶关供电局,广东 韶关 512026)
随着南方(以广东起步)电力现货市场一系列法规的发布,目前广东电力现货市场已经进入了试运行阶段,并实现了现货结算。电力现货建立的初衷是为了实现全社会电力资源的更优配置,目前大约有20%~30%的电力需要通过现货的形式,完成电力从生产到消费这一环节。电力供需紧张关系的波动会引起现货市场价格的波动。在发电厂 售电商 用户这样一条链路中,作为中间环节的售电商会承担现货市场价格波动所带来的收益风险。这是因为对售电商而言,其售给用户的电价是固定的,那么现货市场价格的波动带来的风险将直接传导给售电商:即当电力供需紧张时,售电商从电力现货市场购电价格将可能高于其向用户的售电价格[1]。售电商是一直参与电力现货市场的,加之现货价格波动不会只是短期偶尔出现,所以售电商必然关注长期的利益。综上所述,在电力现货市场下,研究售电商的长期收益具有现实意义。
为尽可能规避现货价格高于售电价格所带来的利益损失,售电商可以借助需求响应[2-4]手段,按照一定的市场价格信号或激励机制[5],诱使用户改变正常的电力消费并减小用电负荷,以减少其从现货市场购电损失。此外,国内外一系列研究表明,用户响应售电商通过发布需求响应,还有助于降低峰谷差,提高系统经济性[6-8],提高其与电厂签长协[9]或月度竞价[9-11]的议价能力。按照用户的反应方式,需求响应可以划分为基于价格型的需求响应[12-13]和基于激励型的需求响应[14-15]。价格型需求响应主要指用户响应用电价格高低调整负荷,可通过分时电价[16]、实时电价[17]、尖峰电价[18]等形式实现,参与的用户覆盖面大,通常需要政府主管部门审议通过再实施。激励型需求响应是发布方通过独立或叠加于零售电价以外的资金等激励措施,使用户及时响应削减负荷[19],包括直接负荷控制[20]、可中断负荷[21]、需求侧竞价[22]、紧急需求响应[23]等。实施激励型需求响应时,只需要售电商和用户两方确定合同,相较于价格型需求响应更灵活,适合于从售电商利益的角度来制订需求响应。
借助需求响应手段,解决售电商和用户的收益最大化问题,从逻辑上可以抽象为多个主体的双方博弈[24]或多方博弈[25]问题。由于售电商是发布需求响应,而用户是响应需求响应,所以售电商占主导地位,而用户则是从属地位,可以采用主从博弈[26-27]的方式来寻找纳什均衡解。然而在现实的电力市场中,特别是电力现货市场形成的初期,参与博弈的各方对外部信息掌握不充分是常态,且各方的决策是一个动态过程,这对采用博弈论来求解问题有着极大的困难。一般在市场形成初期,对个体而言,通常是先做一个试探决策,观察外部环境反应,个体评估决策好坏,再修正决策,这本质上是一种通过学习的方式来获得较优的决策。本文通过引入学习机制来解决多主体的收益最大化问题。当前深度学习算法[2]是研究的热点,具有良好的鲁棒性,离线学习后,能够在新的场景中应用;但深度学习需要大量的数据集进行训练,对于当前还处在起步阶段的现货市场,尚未积累到足够时间长度的数据集,以保障深度神经网络的训练。
鉴于此,本文采用自适应动态规划法[28]来求解售电商和多用户的利益博弈问题,通过一定量的数据集进行离线学习,训练完成后固定神经网络权值,用于在线使用[29]。自适应动态规划法模仿人的思维过程,采用学习的方式,能够在各主体对外部环境信息了解不足的情况下,辅助各主体以逐步趋优的方式进行决策。同时,考虑到研究场景,用户每日最大负荷表现出一定的随机性,通常在其数学期望的30%以内波动。由于自适应动态规划内部的执行网络和评价网络均可采用神经网络实现,具有一定的外延性,针对较小范围内的负荷波动,其决策机构执行网络具有一定的鲁棒性。
1 售电商最优决策
1.1 问题建模
考虑到售电商为需求响应的主导者,用户作为跟随者,处于被动地位,所以先建模售电商的目标函数
(1)
式中:Fr(t)为售电商在第t次需求响应时的收益。售电商通过预估用户的响应电量等,寻优补贴价格pr(t),以最大化式表示的长期收益。
当售电商发布一定的补贴价格pr(t)后,用户根据自身的需求响应潜力、舒适成本等因素,给出最优响应负荷,以实现当前的补贴价格下自身收益最大化。所以对于用户i而言,其目标函数
(2)
s.t. 0≤xi≤Hi(t) .
(3)
式中:Fi,c(t)为用户i在第t次需求响应时的收益;xi(t)为用户i在第t次需求响应时的响应负荷;Hi(t)为用户i在第t次需求响应时的响应负荷上限。
从式(1)和式(2)可以看出所研究的问题是一个多时间尺度的优化问题,售电商关注的是长期收益最大化,而用户作为需求响应的响应者,其关注的是短期的当次收益最大化。式(1)问题采用自适应动态规划法(adaptive dynamic programming,ADP)求解,式(2)采用数学解析法求解。
1.2 ADP的基本原理
ADP优化核心Bellman的最优化原理是:无论过去的状态和决策如何,对于形成的当前状态而言,余下的各个决策必定构成最优策略[30]。基于该原理,将式(1)表示的长期优化问题转化为当前单次求解最优补贴价格的问题。
考虑一个长时间尺度的售电商最优决策求解,假设未来阶段售电商的决策已经是最优,那么针对当前阶段可以求解出最优决策;因此可以认为ADP求解出的决策序列为全局最优决策序列。同时,利用ADP可实现长时间尺度的售电商利益优化问题,并转化为与用户利益优化同一时间尺度的优化问题。定义性能指标函数
(4)
式(4)中γ(0<γ≤1)为折扣因子,反映远期和近期不同时刻售电商收益对总体性能指标函数的影响。考虑到本文离线训练选择的场景中,由于研究场景对应的未来用户负荷存在一定波动,重点考虑近期收益,本文取γ=0.8。
根据式(4),推导出Bellman方程如下:
J(t)=Fr(t)+J(t+1) .
(5)
假设已知第(t+1)次需求响应的最优性能指标函数J*(t+1),那么根据式(5),第t次需求响应时的性能指标函数可表示为Fr(t)+J*(t+1)。根据Bellman最优化原理,求解Bellman方程:
(6)
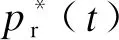
(7)
由于J*(t+1)是未知的,目前还无法求出式(7)的解析解,以下通过迭代法求解式(7)。
1.3 迭代求解Bellman方程
ADP可以利用神经网络逼近性能指标函数J(t),从而可以求解J*(t+1)。ADP中用于逼近的性能指标函数神经网络构成评价网络(critic neural network,CNN),而决策机构亦可由神经网络构成,称其为执行网络(action neural network,ANN )。将CNN络和ANN权值初始化,通过ANN可以求解出初始控制pr,0(t)。相应的性能指标函数
J0(t)=Fr(t)+J0(t+1) .
(8)
控制策略更新为
(9)
根据式(8)和式(9)归纳,对于循环次数m=0,1,2,…,有:
Jm(t)=Fr(t)+Jm(t+1) .
(10)
(11)
ADP算法在式(10)和式(11)之间反复迭代,直至性能指标函数收敛。
1.4 用户最优响应负荷
本节构建用户收益函数,从数学解析法的角度推导出用户最优响应负荷,以方便后续推导ADP效用函数。用户i参与需求响应时,从以下3个方面构建其收益函数:响应补贴、购电成本和响应成本。相关表达式如下:
Fi,c(t)=Ci,e(t)+Bi,c(t)-Ci(t).
(12)
Ci,e(t)=pr(t)xi(t)Tt.
(13)
Bi,c(t)=λr(t)xi(t)Tt.
(14)
式(12)—(14)中:Ci,e(t)为用户i参与需求响应获得的补贴;Bi,c(t)为用户i参与需求响应而减少的购电成本;Ci(t)为用户参与需求响应付出的响应成本;Tt为第t次需求响应持续的时间;λr(t)为第t次需求响应时用户i的购电价格。
用户i参与需要响应削减负荷时,其用电收益受损,这部分成本称之为经济成本,用二次函数表示[1]为
C1i(t)=a1i(xi(t)Tt)2+b1i(xi(t)Tt).
(15)
式(15)中:C1i(t)为用户i在第t次需求响应时的经济成本;a1i和b1i为用户i特性相关常数,与用户参与需求响应经济成本与响应负荷有关。
用户i参与需要响应削减负荷时,要付出舒适用电代价,称之为舒适成本[1],表示为
C2i(t)=a2i(xi(t)Tt)2·λc,i(pr(t-1)).
(16)
式(16)中:C2i(t)为用户i在第t次需求响应时的舒适成本;a2i为用户i特性相关常数,与用户i参与需求响应舒适成本与响应负荷有关;本文将函数λc,i(pr(t-1))定义为带饱和的线性负相关函数,与用户特性相关。
综合上述用户i经济成本式(15)和舒服成本式(16),可得到用户i参与需求响应成本如下:
Ci(t)=C1i(t)+C2i(t) .
(17)
将式(13)、式(14)代入式(12)可得
Fi,c(t)=Ci,e(t)+Bi,c(t)-Ci(t)=
pr(t)xi(t)Tt+λr,txi(t)Tt-b1i(xi(t)Tt)-
[a1i+a2i·λc,i(pr(t-1))](xi(t)Tt)2.
(18)
式(18)中pr(t-1)为已知,当售电商发布后pr(t)亦为已知,由此可知用户i的需求响应收益函数是以用户响应负荷为变量的二次函数。结合目标函数所需满足的边界条件(3),即可得到用户i的最优响应负荷:
(19)
其中:
1.5 效用函数
ADP的效用函数直接定义为售电商收益函数,通过购电成本、售电收益以及补偿费用来构建。
Fr(t)=Bbuy(t)-Cr,e(t)-Cs(t).
(20)
购电成本
(21)
式(21)中:λw(t)为实时电价;n为参与需求用户的数量。
售电收益
(22)
补偿费用
(23)
将式(21)、式(22)代入式(20),可得售电商在第t次需求响应的收益函数
(24)
2 算法框架
采用离线学习和在线使用的策略,解决诸如遗传算法等常规优化算法在线优化时间难满足工程要求的问题。同时,利用神经网络有一定鲁棒性的特点,ADP决策机构能够应对实际场景与学习样本有一定随机偏差的问题。利用一定的历史数据集开展离线训练,过程包含CNN和ANN的交替训练,如图1所示。
创立于1945年的德国雄克公司 (SCHUNK GmbH & Co. KG) 是全球知名的抓取系统与夹持技术供应商。共有超过2 800名员工、9个工厂、位于50多个国家的33家子公司和代理合作伙伴,共同维护并拓展全球市场。雄克可提供11 000种标准部件,包括 2 550款标准机械手;由4 000多种自动化模块组成的完整抓取系统。雄克服务的目标行业包括机械工程、机器人、自动化装配及搬运以及所有知名的汽车生产商及零部件供应商。
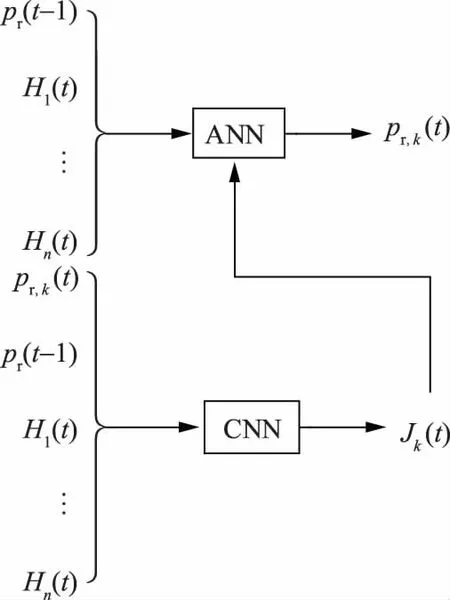
图1 交替训练Fig.1 Alternate training
图1中:变量k表示ADP的第k轮交替训练。用Pi(t)(i=1,2,…,n)表示第t次需求响应时n个用户各自的负荷。对用户i而言,假设其为保障基本需要的最低负荷为Pi,min(t),则有
Hi(t)=Pi(t)-Pi,min(t).
(25)
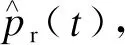
(26)
CNN的输入包含ANN输出的补贴价格pr,k(t)、售电商发布(t-1)次需求响应时的补贴价格pr(t-1)、n个用户在第t次需求响应时的响应负荷上限(H1(t),H2(t),…,Hn(t))。利用第k轮迭代时的CNN权值,可以直接由神经网络的前向计算,得到Jk(t)。
下面说明求解(t+1)次需求响应对应的性能指标函数Jk-1(t+1)。利用训练用的样本数据,得到n个用户在第(t+1)次需求响应时的响应负荷上限(H1(t+1),H2(t+1),…,Hn(t+1))。在ANN训练完成后,可以经过ANN的前向计算,得到pr,k(t)。令Wk-1表示第(k-1)轮训练时CNN的权值矩阵,F表示CNN输入、输出之间的非线性函数,则有
Jk-1(t+1)=F(Wk-1,pr(t+1),pr,k(t),
H1(t+1),…,Hn(t+1)).
(27)
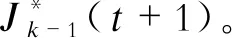
根据Bellman误差方程训练CNN,得到误差函数
(28)
利用神经网络的反向传播法[31],结合式(26),就可以更新相应的ANN和CNN的神经网络权值。
3 算例分析
选择广东省某市5个工业用户2016和2017年的历史负荷数据,筛选其中用电量较高时刻的用户负荷作为售电商发布需求响应前的用户负荷数据进行训练。这些数据带有时标,在针对某时间数据发布需求响应后,其状态转移到下一相邻时间的数据。通过观察用户历史用电数据,确定5个用户在需求响应过程中可以削减到的最低负荷,分别为300 kW、400 kW、300 kW、300 kW、500 kW;5个用户的经济成本一次项系数b1分别为0.57、0.55、0.59、0.64、0.61; 二次项系数a1分别为0.003、0.002、0.001、0.003、0.002;舒适成本二次项系数a2分别为0.008、0.008、0.009、0.008、0.008。
在每训练一次后,都固定输入5组状态-动作对,记录下每次训练后的神经网络输出Jk值,如图2所示。根据5组状态-动作,对输出的Jk值,根据前后2次训练后的绝对误差均小于等于某一个设定值ε(令ε=0.5)来判断训练收敛,如式(29)所示:
|Jk,b-Jk+1,b|≤ε.
(29)
式中b为5组状态-动作对的编号。
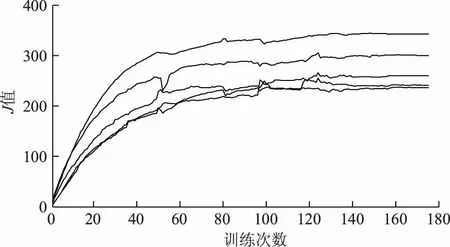
图2 训练过程中的神经网络输出值Fig.2 Neural network output value during training
同时,在每次训练时设置1个最大训练次数,若超过该训练次数仍未收敛,则重新进行训练;若在训练达到最大次数后,由式(29)判断已经收敛,则固定神经网络权值,输入20次需求响应数据进行验证。
图3为根据式(29)得到的神经网络输出值误差。经判断,训练在第172次之后,达到式(29)的收敛要求,此时将ADP神经网络权值固定。
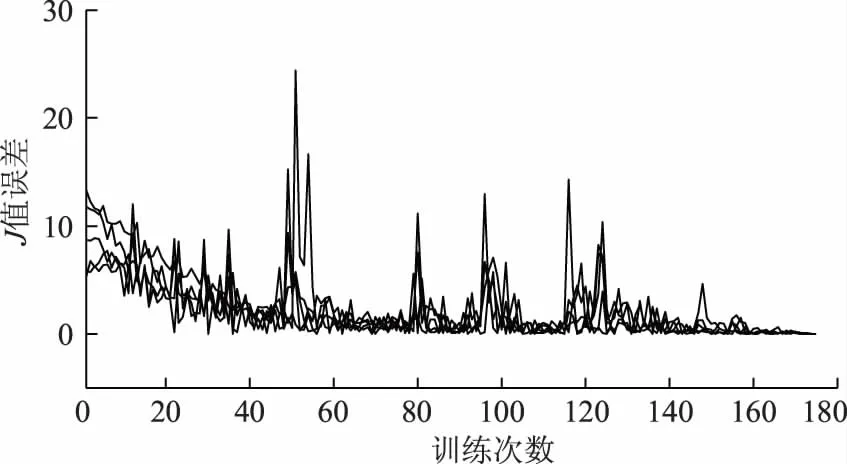
图3 训练过程中的神经网络输出值误差Fig.3 Neural network output value error during training
CNN的神经网络通过训练可学习到用户用电状态转移的规律。由于神经网络具有一定的外延性,针对学习场景和应用场景存在不同初始状态时,所提的方法仍然有效。为了进行验证,修改用户在20次需求响应前的负荷,使用户负荷在初始状态的基础上分别在±10%、±20%和±30%之间波动,这3种情况下共分别验证15、15、7组数据。本文主要结合在初始状态的基础上在±10%之间波动的负荷数据场景,进行仿真分析。
图4所示为初始状态和在该状态基础上波动±10%后状态下,5个用户20次需求响应前的负荷,其中实线表示初始状态数据,虚线表示波动10%的数据。
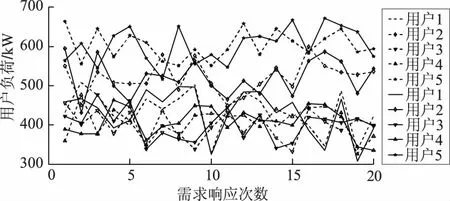
图4 波动前与波动后的5个用户20次需求响应前的负荷Fig.4 Loads before and after fluctuations of five users after 20 times of fluctuations
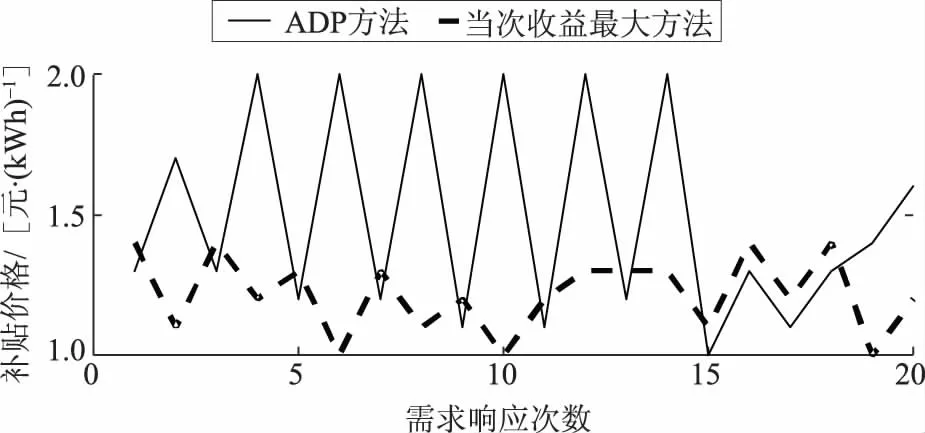
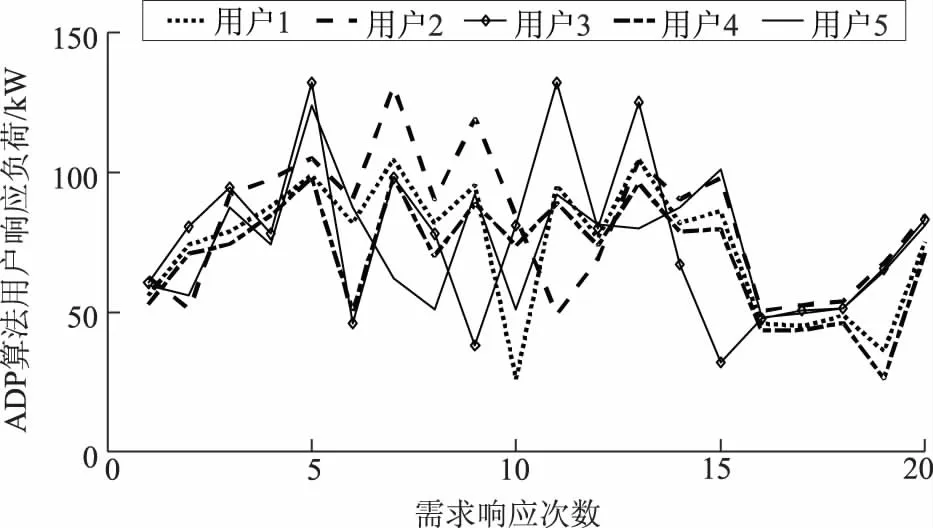
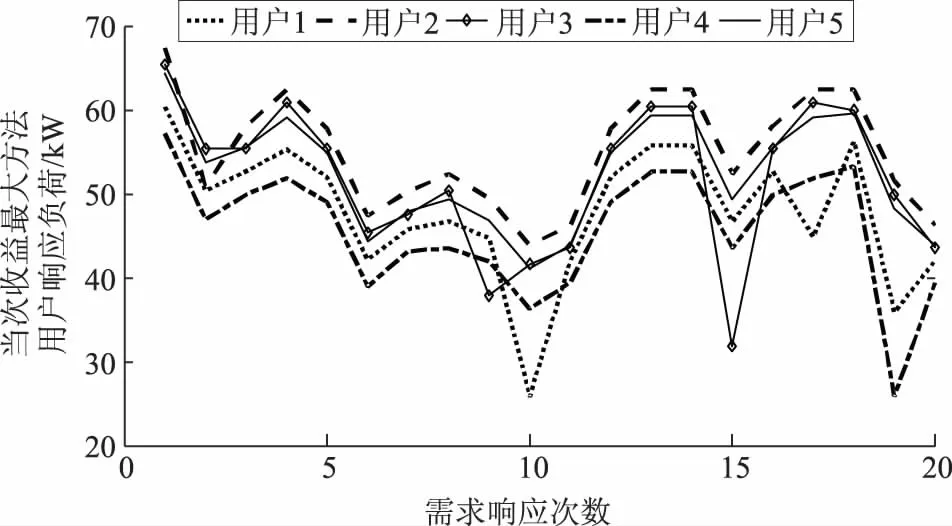
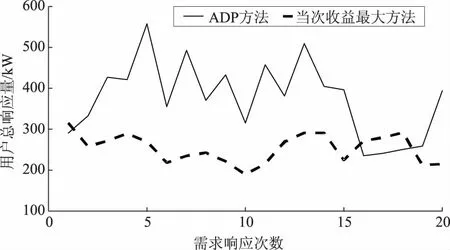
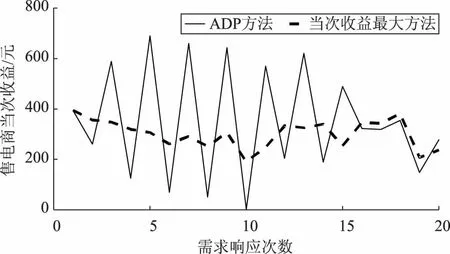
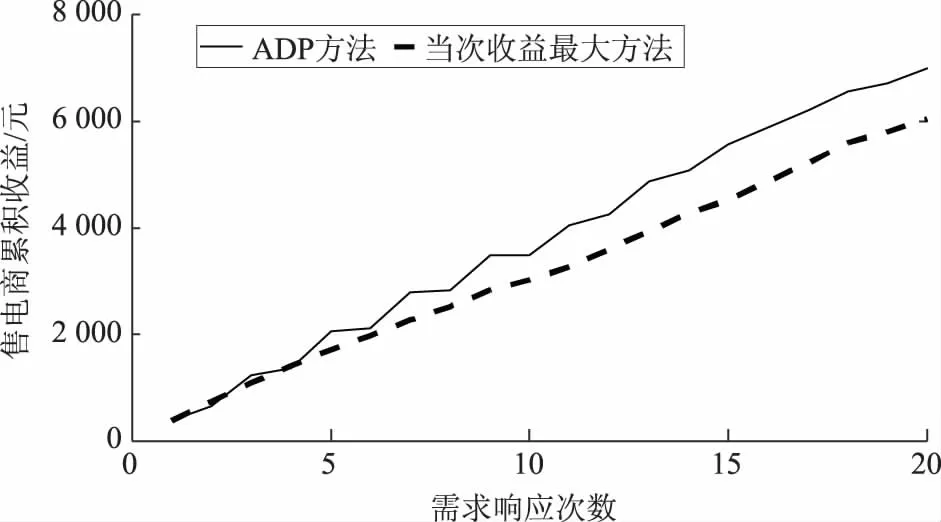
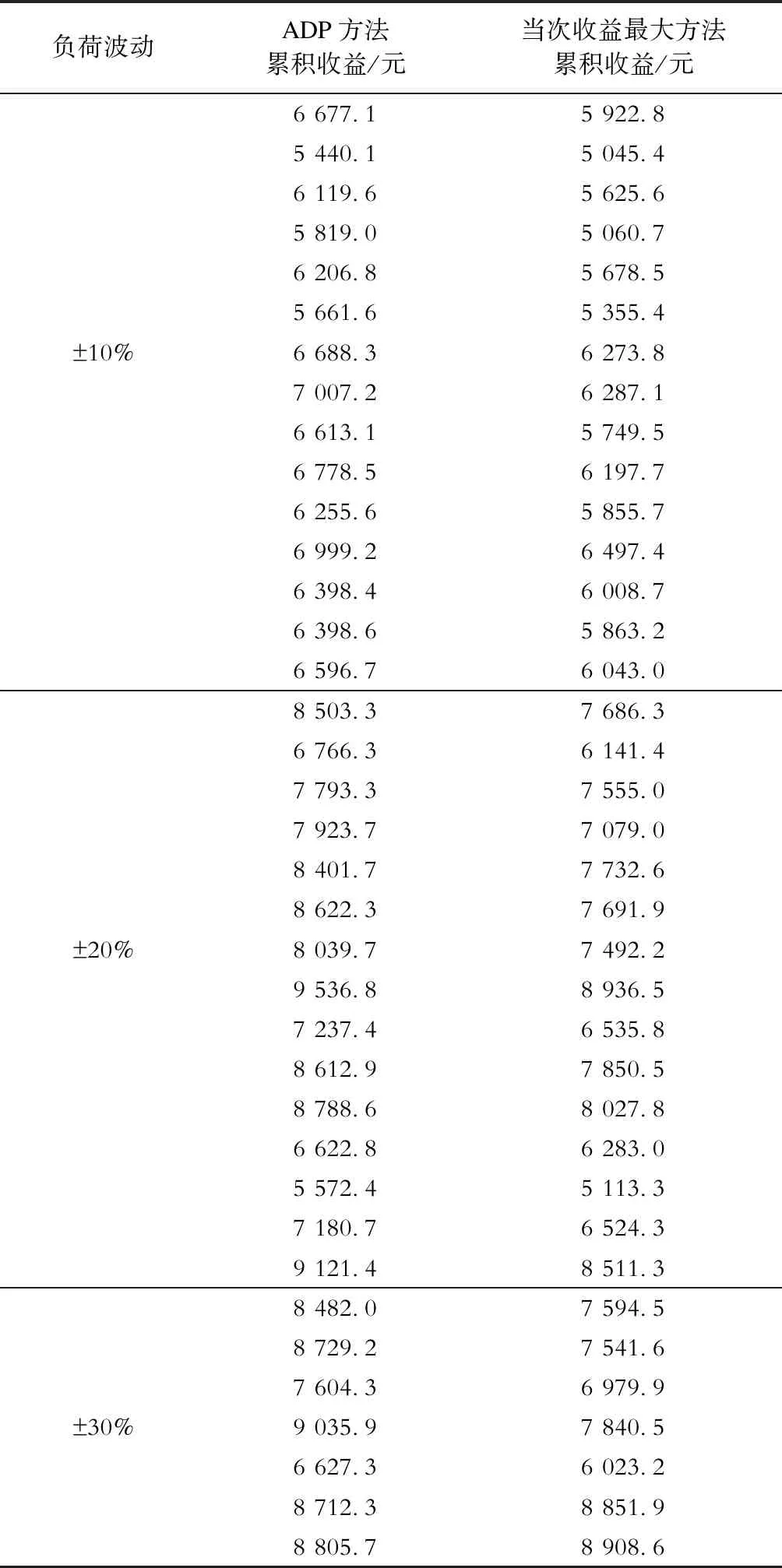
将t-1次发布的补贴价格pr(t-1)对5个用户的舒适成本影响函数λc(pr(t-1))按照图5来表示。当pr(t-1)<0.6 元/kWh时,λc(pr(t-1))=1.7,用户的舒适成本会增加到原基础的1.7倍;当pr(t-1)>2 元/kWh时,λc(pr(t-1))=0.3,用户的舒适成本会降低到原基础的0.3倍;当0.6 元/kWh 图5 5个用户的舒适成本影响函数Fig.5 Five users’ comfort cost impact function 以初始状态对应的数据进行离线训练,将训练好的神经网络权值固定后,把存在波动10%的状态数据输入到训练好的神经网络,前向计算对应J值,找出使J值最大时的补贴价格,分析仿真结果如下。 图6所示为ADP算法和当次收益最大方法分别计算得到的需求响应发布的最优补贴价格;图7和图8分别为使用这2种方法得到的5个用户的响应负荷;图9为使用这2种方法得到的5个用户的总响应负荷;图10和图11分别为售电商使用这2种方法获得的当次收益和累积收益。可以看出,在不同的初始状态下,使用ADP方法依然能够获得更高的长期收益,说明本文模型可以适应不同初始状态的长期收益决策问题。 为验证所提方案的鲁棒性,固定离线训练得到的权值,并进行多次的、不同波动状态的20次累积收益对比,结果见表1。从表1可以看出,在初始状态存在±10%和±20%波动时,ADP方法20次累积收益比当次收益最大方法20次累积收益更高;但是当初始状态存在±30%波动时,上述结论不一定成立,如表1中最后2组数据所示。这是因为波动超出一定范围后,当对应的场景与离线学习采用的场景差异过大时,已经涉及到变结构优化的问题。这种变结构优化问题是后续正在进行的研究拟解决的问题。同时,从目前已收集到的实际工业用户高峰负荷数据来看,暂未发现有正常工作日的高峰负荷存在波动±30%的情况。 图6 售电商在20次需求响应时发布的补贴价格Fig.6 Subsidy price issued by the electricity seller in 20 times of demand responses 图7 ADP方法得到的用户响应负荷Fig.7 User response load obtained by ADP method 图8 当次收益最大方法得到的用户响应负荷Fig.8 User response load obtained by the maximization method 图9 2种方法分别得到的用户总响应负荷Fig.9 The total response load of users is obtained by the two methods respectively 图10 20次需求响应时获得的当次收益Fig.10 Current income obtained from 20 times of demand responses 图11 20次需求响应时获得的累积收益Fig.11 Cumulative gains from 20 times of demand responses 表1 2种方法求解不同波动状态下的20次累积收益对比Tab.1 Comparison of 20 times of cumulative gains from two methods under different fluctuations 本文立足于电力现货市场形成初期,为最大化电力现货市场下售电商的中长期收益,兼顾用户的短期收益,提出了采用基于ADP的售电商动态优化需求响应方案,为未来电力现货市场发展完备提供参考。售电商和用户的收益最大化可以抽象为一个多时间尺度的动态优化问题,根据Bellman最优化原理,将所研究的问题转化为同一时间尺度的优化问题。考虑到售电商发布的历史补贴价格对用户舒适成本感知的影响,构建了售电商与用户前后时间状态耦合的动态优化问题。利用ADP方法良好的鲁棒性,在实际场景与训练场景存在随机偏差时,离线训练得到的策略仍然有效。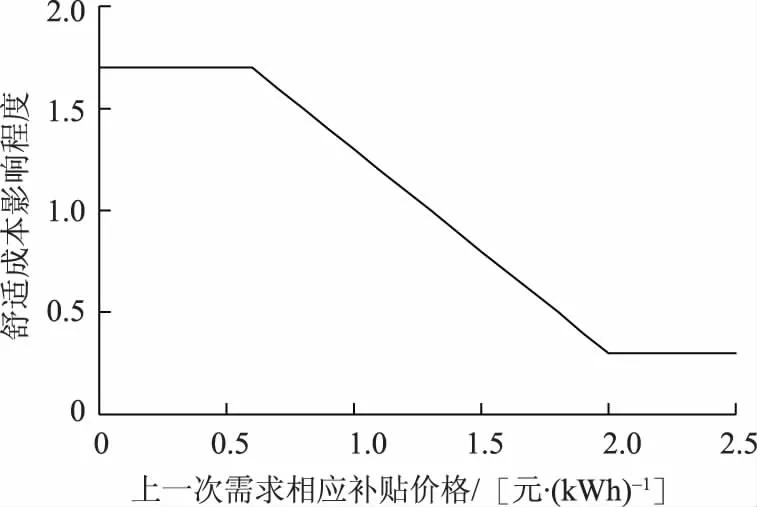
4 结束语

