分时电价下计及用户用电满意度的家庭负荷优化策略

袁晓玲，刘志明，赫卫国

(1．河海大学 能源与电气学院，江苏 南京210098； 2. 中国电力科学研究院，江苏 南京 210003)

随着社会经济的快速发展，家庭用户对电能需求量的快速增长引起电网容量不足，极大地影响电网的安全稳定运行[1]。采用高峰时区域拉闸限电和启动备用发电机组应对该问题，一方面会增加发电成本，另一方面会导致居民生活不便，同时带来环境问题[2]；因此，对家庭用电负荷进行优化调整，引导居民合理用电，降低用电成本，实现电网与用户之间的供需平衡，具有重要意义[3]。

近年来很多国家开始实施分时电价机制。针对分时电价下家庭负荷的优化调度问题，国内外学者从家庭负荷分类[4-5]、优化调度模型[6-7]和求解算法[8]等不同角度进行了研究；然而，家庭负荷设备众多、运行特性复杂，影响了分时电价的实施效果。分布式电源和储能设备的发展，给用户提供了更多的电能来源选择，也给负荷的调度带来了新的问题[9]。针对这些问题，国内外学者对此进行了大量的研究。

文献[10]建立了基于不同电价机制下家庭负荷的经济性调度模型，考虑了家庭设备和分布式光伏的协调。文献[11]考虑用户的用电成本和配电网侧的负荷波动，建立了可调度负荷的智慧社区能量管理优化调度模型。文献[12]考虑功率约束建立最小化电费的用电模型，采用分布式梯度算法求解，实现社会整体效益最大的目标。文献[13-15]分析了电动汽车作为储能装置接入家庭住宅系统(vehicle-to-home)对家庭能源消费的影响。文献[16-18]分析了家庭用户的负载特性，建立用户用电舒适度模型，对用电行为进行优化，没有考虑不同用电设备对用户用电舒适度的影响。

在上述研究的基础上，本文对分时电价环境下家庭负荷的运行优化策略进行分析。首先，对常见的家庭负荷、空调系统、电动汽车建立相应的数学模型，并给出对应的约束条件；其次，建立包含环境舒适度和用电方式舒适度的用户用电满意度评价模型，对考虑用户环境舒适度的空调系统运行策略进行分析，构建不考虑电动汽车充电的基本可调度负荷多目标优化模型；然后，对考虑负荷峰谷差的电动汽车充电策略进行分析，并采用遗传算法求解模型；最后，通过仿真分析，对该优化策略的有效性进行验证。

1 家庭负荷特性分析

考虑未来一天的家庭负荷运行优化策略，将一天平均划分为N个时段，每个时段的时长为Δt。本文取Δt=1 h，则N=24。

1.1 基本用电负荷

基本用电负荷包括家用照明、电视、电脑等，其特点是用户一旦有需求就会开启，不能对其进行优化调度。由于基本用电负荷不可调度的特性，这类用电负荷不会对优化结果产生影响，所以本文不对基本负荷进行优化策略分析。

1.2 可转移可中断类用电负荷

这类用电负荷可以在用户允许的时间范围内随意启动和停止，只要在用户设定的结束时间之前完成用户安排的任务即可；因此，这类用电负荷的可调度区间较大，可以灵活调整其用电计划。其工作特性的数学模型为：

(1)

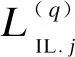
1.3 可转移不可中断类用电负荷

这类用电负荷包括洗衣机、洗碗机等，其可转移特性体现在用户可以选择电价较低的时段让其工作，其不可中断特性体现在一旦开始工作，在工作完成之前不可以中断。这类负荷的数学模型为：

(2)

1.4 空调系统

空调系统占据家庭电能消耗的很大一部分，而且具备功率连续调节的能力，有很大的节能潜力。因为空调系统有间接储能的特性，参考文献[19]，利用经典的热力学交换定律，建立功率损耗与室外温度、室内温度、空调设定温度波动范围约束之间的关系：

(3)

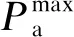
1.5 电动汽车

电动汽车相对于传统汽车来说，具有环保、能源效率高等优点。在电动汽车充电效率ηch一定的前提下，电动汽车充电状态下t时刻的电荷状态S(t)定义为：

(4)

式中：S(t+1)、S(t)分别为t+1、t时刻电动汽车的荷电状态；Pch为电动汽车的充电功率；E为电动汽车电池的额定容量。

为保证电动汽车电池的使用寿命，还要满足以下约束：

(5)

式中Smin、Smax分别为电动汽车电荷状态的最小、最大值。式(5)第1行表示电动汽车的最大充电功率约束；第2行表示电动汽车的荷电状态要保持在一定范围内。

2 负荷优化控制策略分析

2.1 用户用电满意度分析

家庭用户是电力公司重要的服务对象，在对家庭负荷用电策略进行优化分析时，需综合考虑用户对于用电满意度的要求。用户在用电时的满意度包括电量的满意度以及用电舒适度。由于优化前后负荷的工作任务不发生改变，其所需的电量也不改变，因此用户的用电满意度只与用电舒适度有关。用户的用电舒适度又包括环境舒适度与用电方式舒适度。

2.1.1 环境舒适度

影响用户环境舒适度的因素主要包括房间的温度、湿度等。根据范格尔(Franger)教授提出的热舒适度评价过程指标方程，平均热感觉系数(predicted mean vote，PMV)指标[20]代表在同一环境下大多数人的冷热感觉，当PMV值为0时，说明此时的环境为人体学习工作的最佳环境。国际标准组织推荐PMV值为-0.5～+0.5。PMV值与对应的冷热感觉如图1所示。

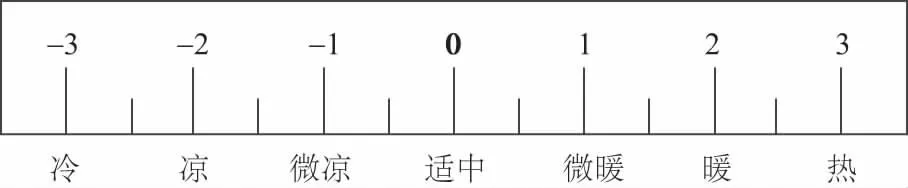
图1 PMV值对应的冷热感觉Fig.1 Cold and hot feelings corresponding to PMV values

在室内湿度、风速最优的情况下，简化后的PMV指标(变量符号M)与室内温度的关系为：

(6)

家用负荷设备中，空调对用户环境舒适度有直接影响，而且空调的耗电量在家庭用电总量中占很大比例；因此，在影响用户环境舒适度的负荷设备中，本文选择空调的运行策略作为主要研究对象。

2.1.2 用电方式舒适度

用电方式舒适度是指优化前后家庭负荷使用时间的改变对用户产生的影响。在不进行优化时，用电负荷的使用时间不发生改变，可认为此时的用电方式舒适度最高；使用时间改变的越多，用电方式舒适度越低。本文将用电方式舒适度定义为优化后负荷曲线的差异，在不考虑空调以及电动汽车的影响下，用电方式舒适度定义为

(7)

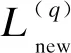
2.2 不考虑电动汽车充电的基本可调度负荷优化策略分析

对于基本可调度负荷，其工作开始的时间可以在用户设定的范围内灵活选择，在不影响用户正常生活的前提下，合理安排其运行时间，可以有效降低用电费用。假设工作过程中基本可调度负荷均为额定功率运行且满足各自的约束条件，考虑用电费用以及用电方式舒适度，目标函数如下：

(8)

式中：Cload为基本可调度负荷用电费用；M为可转移可中断类负荷设备个数；U为可转移不可中断类负荷设备个数；C(q)为q时段电价。

2.3 电动汽车充电优化策略分析

电动汽车作为充电负荷接入电网会增加区域电网的负荷峰值，如果用户单纯追求用电费用最小，将电动汽车充电时间转移到电价比较低的时段，可能会引起另外一个负荷高峰； 因此，对电动汽车充电时间优化时，既要考虑用电费用，又要考虑优化前后的负荷峰谷差。

为更好地分析电动汽车充电行为对家庭日负荷曲线的影响，对电动汽车作如下假设：电动汽车的充电过程为恒功率过程；设定电动汽车电池充满电时的电荷状态为0.9；每次充电用户已知电动汽车充电的所需时长。目标函数如下：

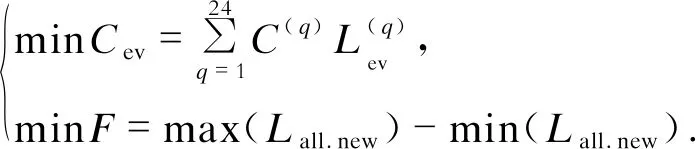
(9)

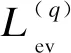
2.4 算法设计

遗传算法也称进化算法。遗传算法是受达尔文进化论的启发，根据生物进化过程而提出的一种启发式搜索算法。遗传算法将要解决的问题类比成一个生物进化的过程，通过编码、选择、杂交、突变等操作产生下一代的解，并逐步淘汰适应度函数值低的解，增加适应度函数值高的解。这样进化多代后就很有可能会得到适应度函数值很高的个体。遗传算法不存在求导和函数连续性的限定，具有内在的隐式并行性和更好的全局寻优能力，已被广泛地应用于函数优化、机器学习、信号处理等领域[21-23]。遗传算法流程如图2所示。

3 算例分析

算例选取的对象为拥有多种用电设备以及电动汽车的单个家庭用户，算例分析参考文献[3]中的分时电价信息，见表1。不同用电设备参数见表2，调度周期为夏季某一日。

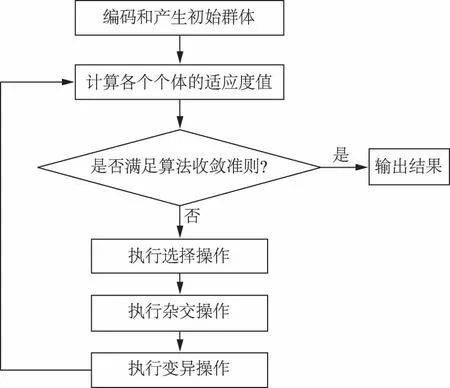
图2 遗传算法流程Fig.2 Flow chart of genetic algorithm

由表1和表2可以看出，峰时段的电价是谷时段电价的3倍，而大部分家用电器的运行时间都集中在电价比较高的峰时段；因此，在保证用户用电舒适度的前提下，对家用电器的运行时间进行优化调度，对于节省电费具有重要意义。

3.1 空调系统优化策略分析

算例选取华东地区夏季某一日的温度数据作为室外温度数据，当天最高气温34 ℃，最低气温26 ℃，全天气温如图3所示。

表1 分时电价信息Tab.1 Time-of-use electricity price

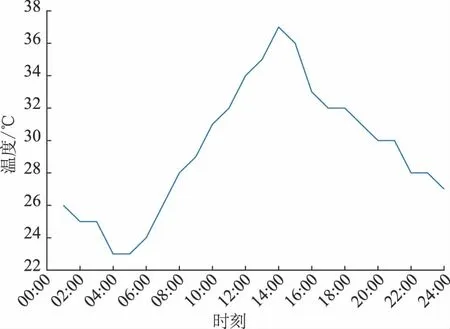
图3 华东地区夏季室外温度Fig.3 Outdoor temperature in summer in east China

表2 用户电器参数Tab.2 Parameters of consumer appliances

根据第2.1节PMV指标与室内温度之间的计算公式，得到室内温度与PMV之间的关系，见表3。

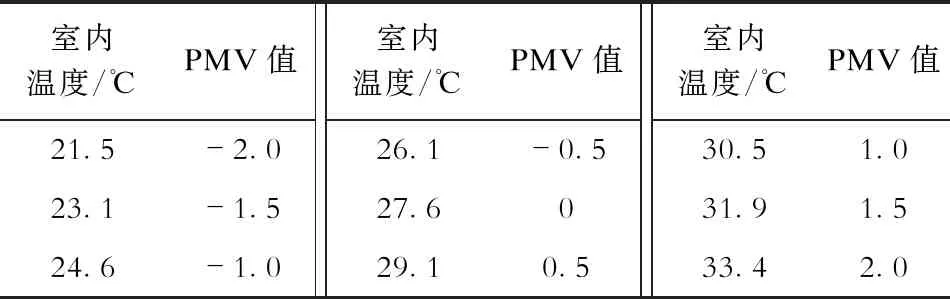
表3 室内温度与PMV之间的关系Tab.3 Relationship between indoor temperature and PMV

由表3以及第2.1节PMV值与人体冷热感觉对应的关系可以看出：当室内温度为26.1～ 29.1 ℃时，PMV值为-0.5～0.5，人体处于热舒适良好的状态；当温度低于24.6 ℃或者高于30.5 ℃时，人体会明显地感觉到冷或热。根据上述分析，夏季将空调温度分别设定为25 ℃、26 ℃、27 ℃，得到空调负荷曲线(图4)和用电费用(表4)，此处假设一日初始时刻的室内温度与空调设定值相同。

表4 不同设定温度下的空调用电费用Tab.4 Electricity cost of air conditioning at different setting temperatures

根据表3和表4可以看出：当室内温度设定为25 ℃时，PMV值处于-1～-0.5之间，此时空调用电费用为14.19元/d；当室内温度设定为27 ℃时，此时的PMV值处于-0.5～0之间，与25 ℃时相比，用户在室内的环境舒适度没有太大变化，用电费用比25 ℃时降低了49.82%，为7.12元/d。因此，后面的分析中将优化后空调的温度设定为27 ℃。

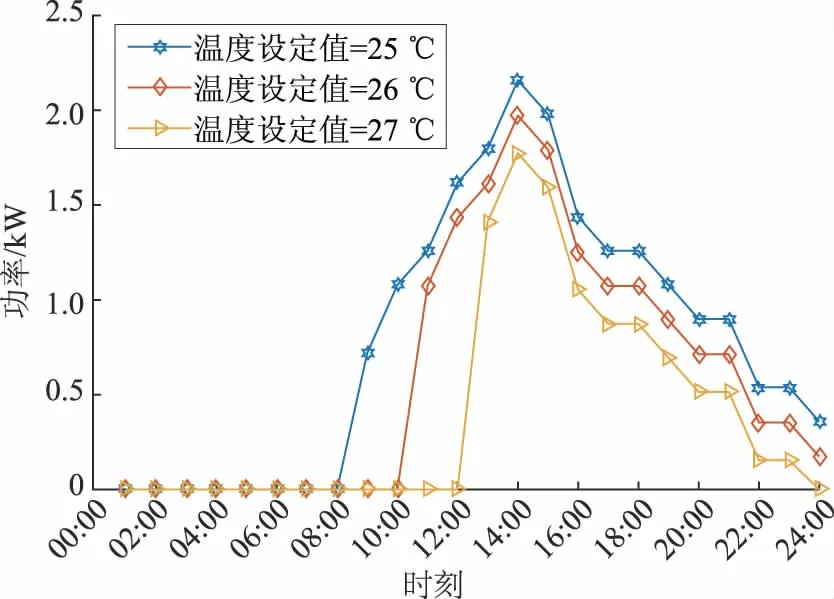
图4 不同设定温度下的空调负荷Fig.4 Air-conditioning load at differentsetting temperatures

3.2 基本可调度负荷优化策略分析

基本可调度负荷包括可转移可中断负荷和可转移不可中断负荷。这类用电设备的相同特性是在用户设定允许的时间范围内，可以将其转移到低电价的时段使用，以节省用电费用。分别以电费最小为目标和以式(8)综合考虑电费和用电方式舒适度为目标(不考虑电动汽车充电，优化前空调的设定温度为25 ℃，优化后空调的设定温度为27 ℃)，利用遗传算法分别对模型进行求解，家用设备的用电状态作为决策变量，得到结果如图5所示。

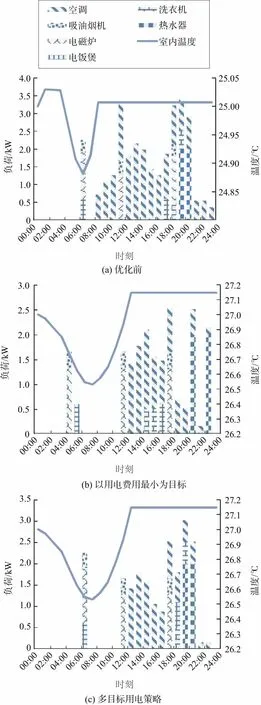
图5 不考虑电动汽车充电的优化前后用电负荷变化Fig.5 Changes of load before and after optimization without EV charging

从图5可以看出，优化前，为了维持室内温度在设定范围内，空调09：00开启，基本上一直处于大功率运行中。优化后，由于用户设定室内温度增加，空调开启的时间由09：00推迟到13：00，同时空调的运行功率减小；其他基本可调度负荷在用户允许的时间范围内被安排到电价较低的时段。与以电费最小为目标的用电策略相比，多目标用电策略中的用电设备使用时间改变较少，电饭煲晚上的使用时间推迟了1 h，电磁炉和吸油烟机晚上的使用时间提前了1 h，其他用电设备使用时间未发生改变，较好地满足了用户的用电方式舒适度。多目标优化后的用电费用为15.6元/d，比优化之前减少了7.73元/d。采用以用电费用最小为目标的用电策略时，用电费用最少(为13.71元/d)，但用电设备的使用时间改变很大，用户的用电方式舒适度最低。

3.3 电动汽车充放电策略分析

在没有任何调控策略引导的情况下，用户对电动汽车充电时间的选择主要受出行规律和生活习惯的影响。根据美国交通部对美国家庭用车的调查结果[24]，电动汽车回到家的时间近似服从N(17.6,3.42)正态分布。假设：用户早上08：00离开家，下午18：00回到家，当天行驶距离所需电量为10.8 kWh；电动汽车在早上08：00之前电量达到最大。同时考虑用电费用与负荷峰谷差，利用遗传算法对式(8)求解，优化前后的电动汽车充电负荷如图6所示，优化前后用户整体负荷变化如图7所示。

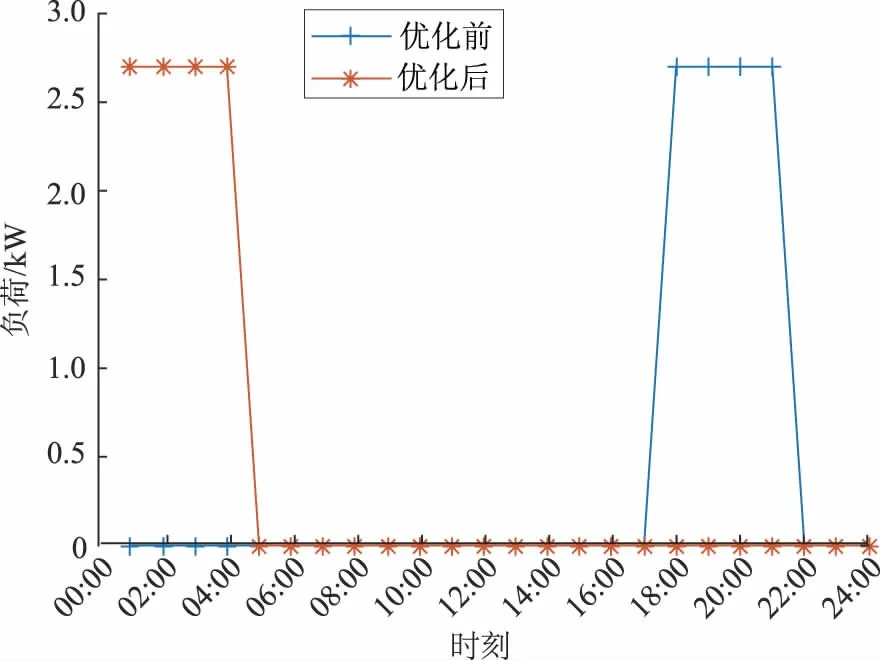
图6 优化前后电动汽车负荷Fig.6 EV load before and after optimization

根据优化前后电动汽车负荷变化以及整体负荷变化可以看出：电动汽车和空调的用电量比其他用电设备更大；在对用电负荷进行优化调度时，应在满足用户用电舒适度的前提下尽可能地降低空调设定温度，减少空调用电量；同时，将电动汽车的充电时间转移到电价较低的时段，降低负荷峰谷差，提高电网运行稳定性；其他负荷的用电时段相对固定，可以在用户允许的时间范围内适当调整运行时间，降低用户用电费用。优化结果见表5。

表5 优化结果Tab.5 The optimization results

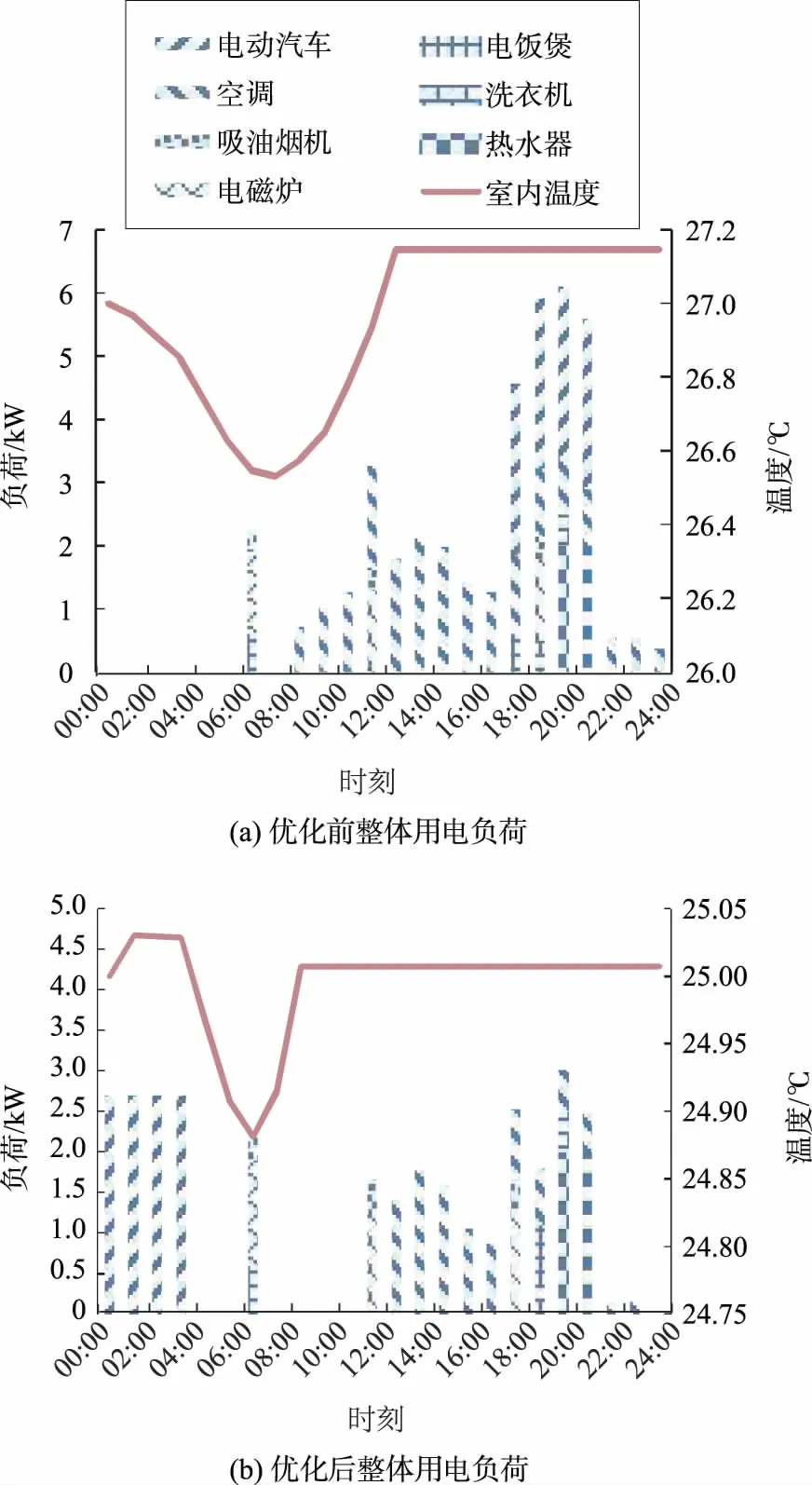
图7 优化前后整体负荷变化Fig.7 Overall load variation before and after optimization

3.4 区域整体优化结果分析

为模拟更加真实的情况，更好地反映不同用户的用电习惯差异，本文选取100户家庭，每个家庭都设置了随机的计划外用电和随机的拒绝优化策略决策。采用本文的优化策略，100个家庭优化前后的负荷曲线如图8所示，100个家庭优化前后的用电费用和电网峰谷差见表6。

从图8和表6可以看出：优化前在电价比较高的时段(19：00—23：00)出现的负荷高峰，经过优化后，转移到夜间电价比较低的时段；在低电价时段没有出现新的负荷高峰，用电峰谷差下降了36.1%；

表6 100户家庭用电费用和峰谷差对比Tab.6 Comparison of electricity costs and peak-valley differences of 100 users

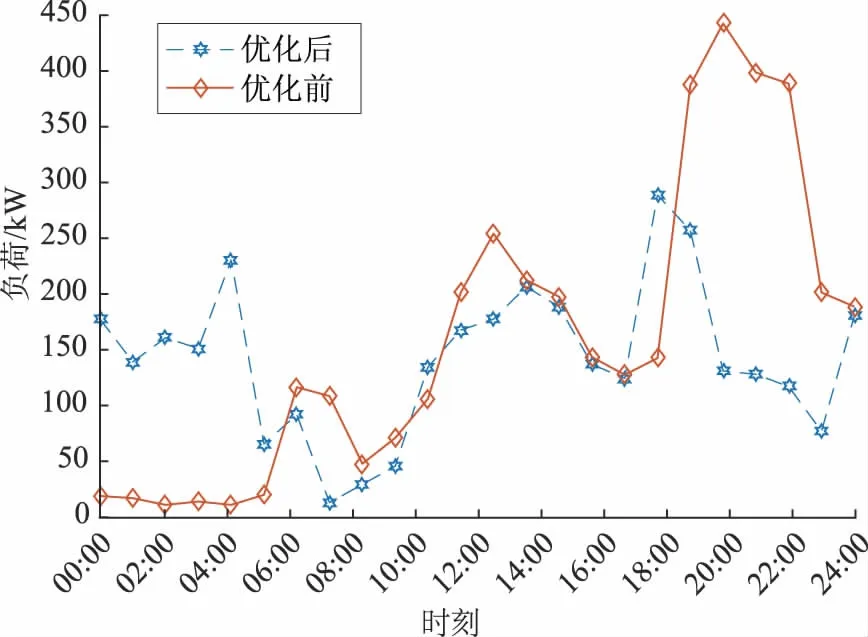
图8 优化前后区域整体负荷变化Fig.8 Overall regional load variation before and after optimization

优化后的整体用电费用比之前减少了640.7元。由此可以看出，此模型不仅对单个用户具有较好的优化结果，对于用电消费习惯不同的规模用户依然有良好的优化效果。

4 结束语

本文基于分时电价环境，考虑空调系统对用户环境舒适度的影响以及电动汽车充电负荷转移对负荷曲线峰谷差的影响，建立家庭用电设备调度模型。算例仿真表明该优化模型在满足用户用电满意度的前提下，通过调整不同用电设备的用电策略，可以综合考虑用户的舒适性和用电经济性，为用户提供个性化的用电方案。将该模型应用到区域整体用电优化中，加入用户计划外用电和用户自行抉择是否接受优化策略，使仿真更加贴近实际情况，结果表明该用电优化策略能够有效降低用户侧用电费用并起到削峰填谷的作用，实现电网和用户双赢。