基于图注意力深度神经网络的癫痫脑电尖波识别

崔昊天，宋 森,2,3

(1．清华大学 脑与智能实验室及生物医学工程系，北京 100084； 2．北京未来芯片高精尖中心及清华大学类脑计算研究中心，北京 100084； 3．清华-IDG/麦戈文脑科学联合研究院，北京 100084)

脑电(electroencephalograph, EEG)是癫痫诊断和治疗评价的重要临床手段[1]。脑电中的棘波、尖波、慢波等是临床中确认癫痫发生和癫痫病灶定位的重要指标。尽管费时费力，人工识别依然是临床中分析脑电记录的常用方法[2-5]。

为了实现脑电自动识别分析，相关研究者提出了多种识别算法。总体上可以划分为以下几类：模板匹配[2, 6]、时频谱分析[7-9]和人工神经网络方法[5, 10-11]。这些方法对尖波的自动检测取得了进展，但存在着假阳性高及需要人工选择特征的缺点。如Gotman[12]通过筛选特征后降低识别伪差概率，但假阳性率仍达10%。因此算法很难对完全正常不含尖波的脑电记录作出准确判断，影响临床的应用。

简言之，由于脑电信号存在幅度微弱、信噪比较低、伪影干扰多、多受试和多次测试间的变化大等难点，传统上基于人工特征选择的方法不足以得到有效和能泛化的结果。因此，近年来以深度学习为代表的机器学习方法转而完全从数据出发[13-15]，带来了解决上述难点的新的可能。然而考察已报道的深度学习方法，处理多通道的脑电数据仍存在不足。其中一类不考虑通道间的信息，只用到通道内信息进行识别[13]；另一类利用多通道信息，如强制遵循数据中既定的通道排序进行卷积，忽略了脑电图记录中相邻的通道并不代表其在生理或病理中的相关性这一事实[14-15]。实际上，相比按照电极的排列顺序，有研究认为从信号中挖掘通道间的相关性更有效。例如Gotman等[16]和Wendling等[17]报道相干系数(coherence)和非线性相关系数(non linear correlation)可以作为衡量脑连接网络(connectivity network)的方法。Douw等[18]分析发现癫痫病灶区域内电极间的相位延迟指数(phase lag index)增大与癫痫发作有正相关关系。

基于上述分析，本文提出一种不依赖人工特征的图注意力深度神经网络算法，能够数据驱动地学习和利用电极通道间的关联关系实现尖波识别。与以往方法不同，本方法将脑电数据建模为关系图数据，即将各电极通道的记录，建模为记录时序信息的数据节点，而各节点之间的关系强弱由模型后续根据参数学习得出。在算法中，既能够提取通道内的多尺度时序特征，又能够提取通道间的关联关系。通过两方面特征实现准确的尖波识别。

1 数据和方法

1.1 数据来源与形式

本研究所使用的数据来自清华大学附属玉泉医院癫痫中心，包含20组头皮脑电记录数据。数据采用国际标准10～20系统记录，采样率500 Hz；后经专家标注出282次尖波事件，平均每次事件含有5.2个电极记录到尖波，合计1482个正例(有尖波)样本。

对于数据的预处理主要包括了滤波、归一化和截取窗口3部分。针对尖波识别任务，首先采用3～70 Hz带通FIR滤波器滤波，并降采样至200 Hz；其次将各通道信号减去参考电极A1，A2的平均值，再除以单次记录所有信号的标准差进行归一化；之后，以窗口长度0.6 s，步长0.06 s进行滑动窗口截取。对于中心0.3 s尺度内出现尖波事件的窗口，标注为正例样本。于是得到本文使用的训练集。

正式地，数据集的形式如下：

D={(X1,y1),...,(XN,yN)}

(1)

其中N代表总样本数。二维矩阵数据Xi∈RE·T为单个样本窗口的脑电信号，包含E个电极通道和T(=120，即0.6 s)个时间点的数据。二值向量yi∈{1,0}E为对应每个电极通道上是否出现尖波的标注记录。

最终数据集包含4482个窗口片段样本，每个窗口含18个有效数据通道，经统计，有尖波发生的通道占数据总量的14.06%。

1.2 算法概述

为解决脑电中尖波放电识别问题，本文提出一种端到端学习的深度神经网络算法。本算法由依次层级相连的3部分组成：1)卷积编码层；2)图注意力层；3)全连接输出层。式(1)表述的固定长度窗口的多通道时序脑电信号作为算法输入，依次经过3部分计算，输出对每个通道上是否有尖波的预测结果。

1.2.1 卷积编码层(通道内)

卷积神经网络[19]利用多组共享的卷积核提取数据中的特征，形成输出特征图，具有很强的特征提取能力，在近年来引领了深度学习和计算机视觉技术的发展。本文首先使用多层卷积网络提取脑电信号中时序维度上的形状特征。对于一维卷积，其输入为三维矩阵input∈RN·Cin·L，输出为output∈RN·Cout·Lout，具体计算方法如下式表述：

(2)

其中weight和bias均为卷积核的可学习权重。在本文中首层的input为脑电窗口数据Xi∈RE·T，故N=E,Cin=1,L=T。在脑电信号处理中，Schirrmeister[14]指出脑电信号中包含了多种时间尺度的信息，适合用多尺度的卷积核提取特征。本文设计了3层变尺度的卷积网络在时间维度上提取通道内的各尺度特征，见于图1中的卷积编码层示意。其中第二层和第三层卷积分别对应了原信号中约10 ms和40 ms的特征尺度，这一特征尺度经验性地包含了尖波上升下降沿发生的时间范围。

1.2.2 图注意力网络层(通道间)

图是一种高维的数据形式，由节点和描述节点间关系的连边组成，诚如本文在引言中指出的，脑电数据各电极通道采集的数据间可以认为存在关联关系。本文利用下述图注意力网络层提取各通道间的关联关系作为特征提升后续尖波识别效果。

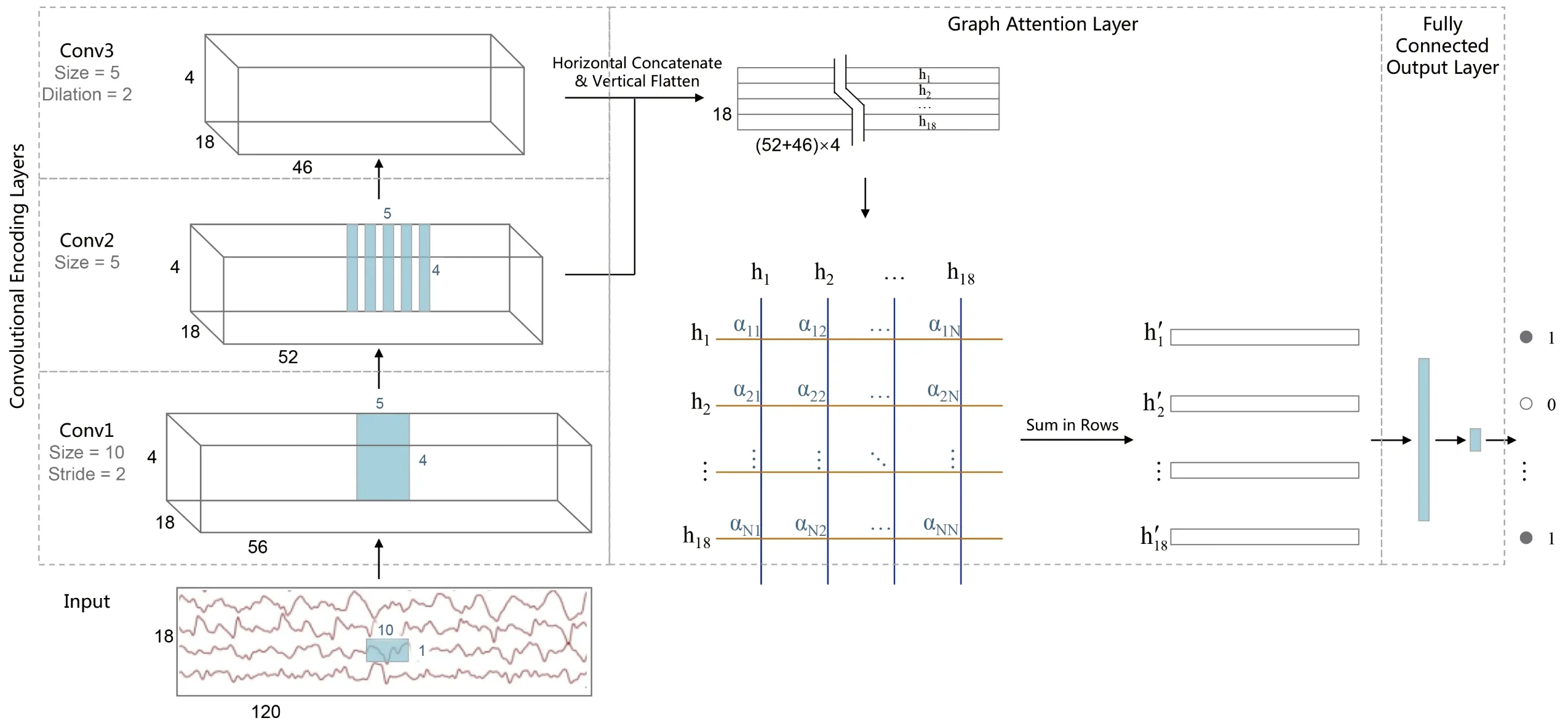
从左到右分别为卷积编码层(通道内)，图注意力层(通道间)，全连接输出层

from left to right is the convolutional encoding layer (inner-channel), the graph attention layer (inter-channel), and the fully connected output layer

图1模型结构示意图

Figure 1 The schematic diagram of the model

图数据上的深度学习是现阶段深度学习研究的热点之一，其中Velickovic等[20]提出了一种由可学习的自注意力方法[21]刻画图上节点之间关联关系的神经网络结构。基于上述方法，本文中为了描绘通道间的相关关系，引入并改进了图注意力网络层，具体而言：图注意力网络的输入为一组节点向量h={h1,h2,...,hN},hi∈RF。在本任务中此输入即为卷积编码层的输出。对于节点向量，首先通过一个共享的线性变换W∈RF′·F，再通过一个共享的注意力函数a:RF′·RF′→R作用在向量对之间来计算注意力系数：

eij=a(Whi,Whj)

(3)

对于尖波识别，发现对于两通道的脑电信号，其变化规律是否同步为一重要特征。因此，在原有图注意力计算函数的基础上做出如下改进：

eij=a[Whi,Whj,(WhieWhj)]

(4)

其中，e表示向量的按位相乘。在算法实现中函数a通过全连接神经网络实现。此注意力系数表征了节点j的特征对于节点i的关联程度。为了使得在不同节点间此系数可比，这里利用softmax函数对其进行归一化：

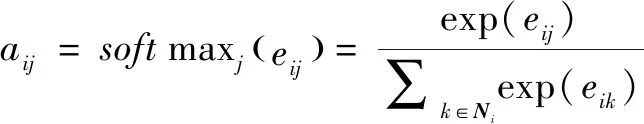
(5)

其中，Ni表示节点i的邻接节点，本研究中认为各电极间均有潜在可能关联，即Ni包含所有节点。

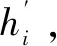
(6)

又经实验发现，引入多组并行的注意力系数能够提高网络学习的稳定性和算法性能。故，最终图注意力计算过程如下式，

(7)

其中‖表示向量的拼接。图注意力网络层的具体设置，如图1中图注意力层部分所示。在后续实验中，均设置K=4。

本文首次利用图注意力做通道间的关联分析。一方面，图注意力层能够考虑到尖波特征在通道间是共同或同步发生的特征，使得尖波识别的准确率提升；另一方面得到的通道间的相互注意力数值，也可以作为通道节点间的一种相似性度量。由此得到的注意力关系图，具有潜在的指示意义(见2.3)。

1.2.3 全连接输出层

输出层为两层的全连接网络。其输入为图注意力层的输出向量，输出为各个通道的类别分类概率(两类：是否包含尖波)。其中全连接第一层输出维度为10，激活函数为elu[22]。全连接第二层输出维度为2，激活函数为softmax。

全连接层的计算过程使用同一组参数对每个通道的特征向量并行计算，通道间无特征共用。

1.3 训练方法

上述整体网络如图1所示。本研究中使用预测概率和标注之间的交叉熵损失函数为目标进行训练。选择学习率为0.001的Adam[23]优化方法进行优化。每轮迭代使用64个样本批处理。在训练集上重复优化迭代，至收敛后停止，此过程需要约600次重复。

2 结果与讨论

2.1 性能评价

本实验对于数据集均进行5折交叉检验，并使用准确度、敏感度和特异性3个指标衡量性能。其定义如下：

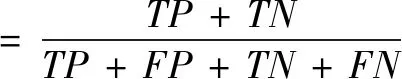
(8)

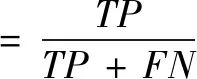
(9)

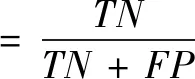
(10)

其中，T和N分别为正确和错误检出，P和N分别为有和无尖波。

同时，引入SVM和BrainDecode两种基线方法作为对比。SVM方法是利用样本各窗口的数据，取各通道每0.05 s内的能量均值作为特征输入，由支持向量机输出类别判断。BrainDecode方法是Schirrmeister[14]提出的卷积神经网络方法在本任务形式下的变体。最终各方法的性能对比(表1)显示均为5折交叉检验的均值结果。其中GADN表示本文提出的图注意力深层神经网络。GADN_OnlyConv指在图注意力网络中只使用设计的卷积编码层，不使用图注意力层的模型。

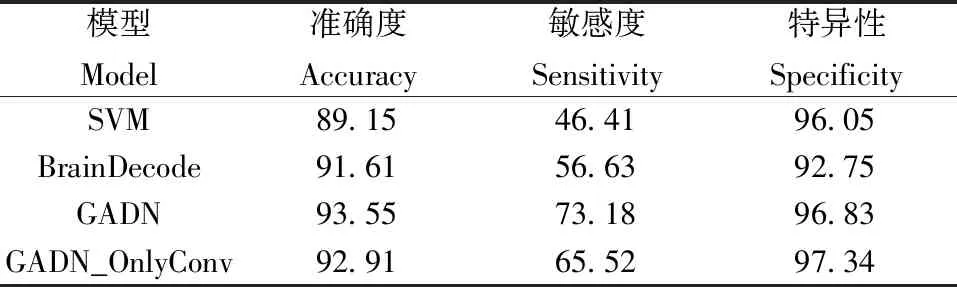
表1 各模型性能对比

综合表中信息可见，本文提出的图注意力深度网络在各个指标评价上均优于对比方法。特别是其在敏感性唯一高于70%的同时，假阳性率(假阳性率=1-特异性)仅约为3%。另外对交叉检验的5组数据进行显著性t检验发现，GADN_OnlyConv与GADN相比准确度和敏感度明显下降(P值均小于0.01)，说明图注意力层得到的通道间的关联特征对于尖波识别任务有明显意义。同时，在测试中发现GADN对正向和负向的尖波均能做出识别。

2.2 图注意力层的作用分析

为了直观检视GADN模型中图注意力的作用，本文进行了如下实验：选择测试数据集(共896个样本)上的脑电数据通道中不含尖波的背景通道进行数据消除(通道信号置0)，再将消除后的数据输入模型进行计算。分别消除0个至9个通道，考察模型的敏感度变化。值得注意的是，由于GADN中的卷积编码层完全作用在通道内，于是对于未被改变的正例通道，卷积编码层的输出不会发生变化。因此，在分析实验结果时，敏感度的变化可以认为完全反映了图注意力网络在通道间信息改变时的输出变化。

实验结果见图2。其中GADN_OnlyConv只有通道内特征，其敏感度不会因背景通道去除受影响，这里与GADN形成对比。观察发现，在逐渐去除背景通道时，GADN输出的敏感度明显上升约17%。换言之，图注意力层在去除背景通道信息时，因缺失通道间输入并不发挥明显作用，此时与通道信息完整时相比，模型敏感度显著升高。

以上实验现象说明，全通道输入的正常情况下，GADN中的卷积编码层(通道内)和图注意力层(通道间)有互补作用，图注意力层起到对备选尖波的明显筛选作用。卷积层的敏感性高特异性低，首先会选出足够多可能为尖波的备选(敏感度接近90%)，之后图注意力层根据多个通道间的综合信息减少尖波的输出，进而实现更高的特异性。以上再次说明了通道间关联特征的重要意义，以及图注意力层优异的关联特征提取效果。

2.3 对电极间注意力关系的解释

图注意力网络中得到的注意力系数在尖波识别中描绘了通道间的关联特征，自然地可将其视作一种电极通道间的距离度量。为了探究此度量的应用意义，引入如下实验：本文选取了一组典型癫痫间期的脑电记录，共60 s。根据医生标注，此段记录中出现了多次重复的尖波，集中发生在T3、T5、C3和F3电极。将GADN模型应用于本段数据的尖波识别，并在计算过程中记录注意力系数。考察在每次尖波检出时刻的注意力系数，求其均值以此作为各电极间的距离度量。通过t-sne[24]投影到2维平面得到图3。

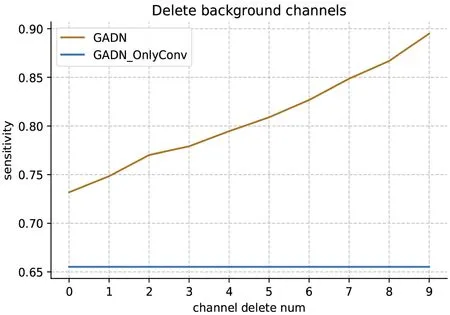
图2 敏感度随通道去除数目变化折线图Figure 2 Sensitivity line chart as the number of channels removed increases

从图3中可以看出，在由注意力画出的电极通道关系图中，发生尖波的电极明显地聚集，并分离于背景电极。可以认为，图注意力网络通过电极间的注意力关系描绘了和任务(尖波识别)相关的距离度量。由于尖波的发生对于判断电极所在区域是否为癫痫病灶有重要意义。GADN通过参数学习得到的上述注意力关系投射，有潜力描绘出尖波发生电极的聚集，对临床诊断中的病灶定位有潜在的重要意义。

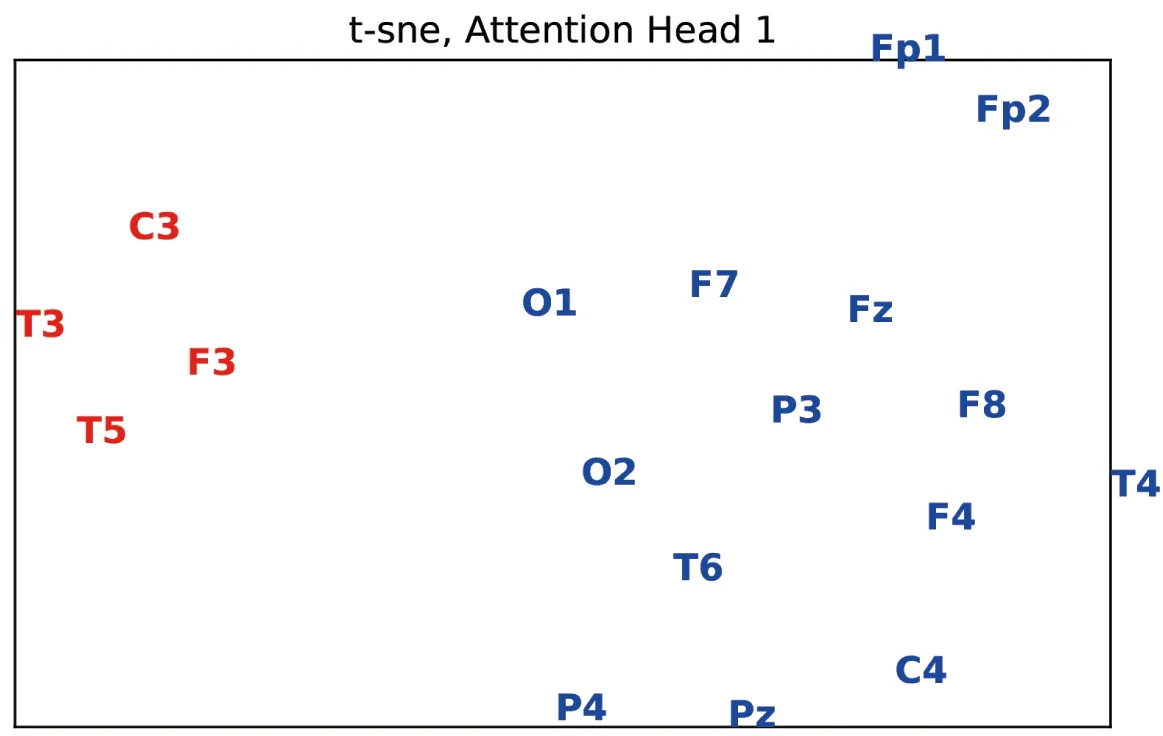
距离由注意力获得，观察到含尖波的电极(红色)有明显的聚集

图3注意力关系图-节点对应电极
Figure 3 Attention relation graph-Nodes represent electrodes

3 结论

现有的脑电尖波识别方法多关注于挖掘电极上信号的特征，对于电极之间的联合分析或特征学习少见报道。本工作首次利用和改进图上的图注意力神经网络，并首次提出了一种能够联合分析多电极的深度神经网络尖波识别方法。在与多种见于报道的方法对比中，实现了领先的准确率，敏感度。同时本算法能够得到和尖波放电明显相关的电极关系图，对临床诊断分析有潜在的重要指示意义。

致谢：感谢清华大学附属玉泉医院癫痫中心周文静主任和刘一鸥医生提供实验所用头皮脑电数据，以及相关标注。在本文的写作中，感谢清华大学医学院洪波教授多次在脑电与癫痫领域知识方面给予的无私指导。