长短期记忆神经网络在叶绿素a 浓度预测中的应用

石绥祥，王蕾,2*，余璇，徐凌宇

( 1. 国家海洋信息中心 数字海洋实验室，天津 300171；2. 国家海洋局东海信息中心，上海 200136；3. 上海大学 计算机工程与科学学院，上海 200444)

1 引言

叶绿素a 浓度作为水质状况及富营养化程度的衡量指标，一直是水质监测的重要参数[1–3]，是判断赤潮发生与否的重要因素，因此越来越多的科研人员投入到对叶绿素a 浓度的预测研究中。而限于早期叶绿素a 浓度相关数据的匮乏，对叶绿素a 浓度的预测大致可以分为两类方法，其中一类方法为统计学方法，这一类的方法最先由加拿大专家Vollenweider[4]提出，他利用了统计模型来预测富营养化问题，但是这一类传统的统计方法只能求解某一要素的平均浓度分布，无法模拟相关因素与叶绿素a 的影响关系；另一类方法主要是以生态动力学为理论依据，基于对流−扩散方程建立模型[5]来预测叶绿素a 浓度，此类方法的优点是考虑了自然界中多种因素间的相互作用，但生态动力学模型有一个共同的缺陷是其包含太多参数，而这些参数的设定十分依赖对于特定问题的经验，并且难以确定合适的参数。

随着数据量和种类的增多，收集的数据也越来越多，传统的统计学习方法越来越难以适应，鉴于神经网络及深度学习在大数据量及复杂场景中，对于特征的表达能力，越来越多的学者开始利用神经网络及深度学习对叶绿素a 进行预测。人工神经网络是一种模拟生物神经网络信息处理功能的信息处理模型，也是一个高度复杂的非线性动力学系统[6]。在此类研究中，最具代表性的人工神经网络模型是反向传播神经网络(Back Propagation Neural Network, BPNN)，赵玉芹等[7]利用BP 神经网络成功地对渭河水质参数进行了遥感反演；卢志娟等[8]利用BP 神经网络实现了对西湖湖心区叶绿素a 浓度的周预测；周露洪等[9]通过对2006−2008 年的常规水质参数进行主成分分析，建立BP 神经网络模型对叶绿素a 浓度进行月预测；杨柳等[10]利用BP 神经网络对温榆河进行了水质参数反演，反演结果优于传统线性回归模型。应用广泛的BP 网络大多只考虑相关因素对叶绿素a 的影响关系，而忽略了所有影响叶绿素a 的因素在不同时延上影响关系的差异性，无法动态的依赖历史时序信息进行叶绿素a 浓度预测，并存在局部极小、收敛时间过长从而泛化能力差的问题[11]。

Dekker 等[12]建立了叶绿素a 浓度与TM 影像的线性和指数回归模型，指出指数模式要优于线性模式，但TM 的分辨率较低，不利于水质参数监测，且T 的波段组合缺乏物理解释；柴永强等[13]利用决策树模型智能检测赤潮现象，采用机器学习技术训练检测赤潮的决策树分类模型，此模型对渤海等海域取得了较满意的结果，但是决策树模型对缺失数据处理比较困难，也容易出现过拟合现像；李修竹等[14]采用支持向量机的方法，以温度、盐度等8 种要素作为输入，叶绿素a 浓度作为输出对叶绿素a 浓度进行预测取得了较好的结果，此种方法虽然避免了神经网络方法的局部极小值问题，但是对核函数的高维映射解释力欠缺。

基于目前的研究成果，本文在海洋数据多要素关联关系的基础上，提出了一种结合时序方法的递归神经网络智能预测模型，对判断藻类赤潮的重要指标叶绿素a 浓度进行预测，以解决传统的递归神经网络的梯度消失或爆炸问题。

本文的创新点主要集中在两个方面：（1） 量化不同要素对于叶绿素a 浓度在不同时延上的关系，依据长短期影响关系将其分类；（2） 对于不同的类别要素，构建差异性的子网络对其分别建模，每个子网络采用不同的训练方式，利用融合层将不同子网络的特征进行融合以得到更为稳定准确的结果。

2 数据来源与研究方法

2.1 数据来源

近年来，三都澳水产养殖的开发利用几乎是直线上升，宜养面积的利用超过100%，由于三都澳是一个口小腹大的内湾，一般海水进行一次完全循环要1 周，垃圾在海面上漂流很长时间，沉积慢，严重影响了海区环境卫生，影响海区水交换，使水域污染日益严重，超过水域的自净能力，导致海水富营养化加剧，病害发生频繁，因此本文选取三都澳的连续监测资料作为本文的实验数据，其中三都澳站位数据时间段是从2015 年5 月12 日至2015 年7 月2 日，监测要素包括表层温度（WD）、PH、电导率（DDL）、叶绿素（YLS）、浊度（ZD）、溶解氧（RJY）、盐度（YD）、电压（DY）共8 个，监测频率的时间间隔为5 min 一次，站位分布情况如图1 所示，图中红色位置是三都澳站点所在位置。

2.2 研究方法

本文利用长短期记忆（Long Short-Term Memory,LSTM）模型强大的长短期记忆能力分析三都澳站位水质监测数据，选择对三都澳水质影响较大的因子网络模型，预测三都澳站位的叶绿素a 浓度的变化趋势，从而为有效及时地控制水质提供科学依据，总体研究方法由图2 所示。

从图2 中可以看出本文提出的模型一共分为3 层：数据分析层、模型层和决策层。其中数据分析层为原始数据的预处理，第二层模型层包含自相关性分析、多要素与叶绿素a 的关联关系分析、长短期依赖时间分析以及构建融合的LSTM 预测模型，第三层通过对预测分析结果的反馈来提供的有效分析决策。

3 数据预处理

3.1 数据归一化方法

由于各要素原始数据的量纲及数量级不同，在进行数据相关性分析和网络训练前要先对数据进行归一化处理。

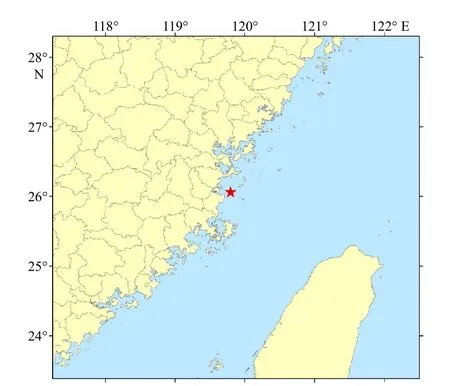
图 1 三都澳站位分布Fig. 1 Station location distribution map of Sandu Ao

经过标准化处理后的数据一般在0 到1 之间，这样有利于网络训练，在量纲统一的基础上为下一步相关性分析和网络训练奠定基础。

3.2 自相关分析方法

在进行叶绿素a 浓度预测前，首先需要知道叶绿素的自相关情况，以便在后面的网络训练和预测过程中如何考虑其自相关情况。

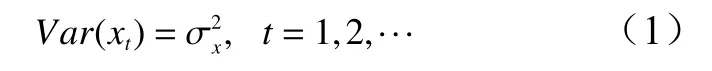
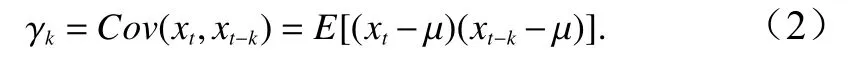
相隔 k 期的两个变量 xt与 xt−k的协方差即滞后 k期的自协方差可以定义为：程的自协方差函数。当 k =0 时， γ0=Var(xt)=自相关系数的定义如下：

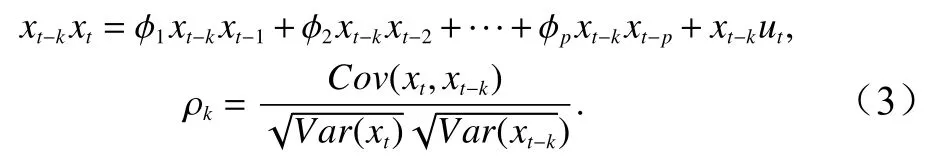
4 构建融合的（Merged）LSTM 模型

4.1 多要素间关联分析方法

m×n

散布矩阵为 的半正定矩阵如下：

其中 T 表示矩阵的转置，散布矩阵可以简要的表示为S=XCnXTCnXT，在此 Cn定 义为定心矩阵，其中 Cn公式如下：

式中，O 表示所有元素都是1 的矩阵；在最大似然估计中，给定 n个样本，一个多元正太分布的协方差可以表示为归一化的散度矩阵：

4.2 长短期依赖时间分析法

X 、 Y （也可以看作两个集合），它们的元素个数均为N （ N 表示时间序列的长度），两个要素取的第i(1 ≤i ≤N)个值分别用 Xi、 Yi表示。对 X 、 Y进行排序（同时为升序或降序），得到两个元素排行集合 x 、 y ， 其中元素 xi、

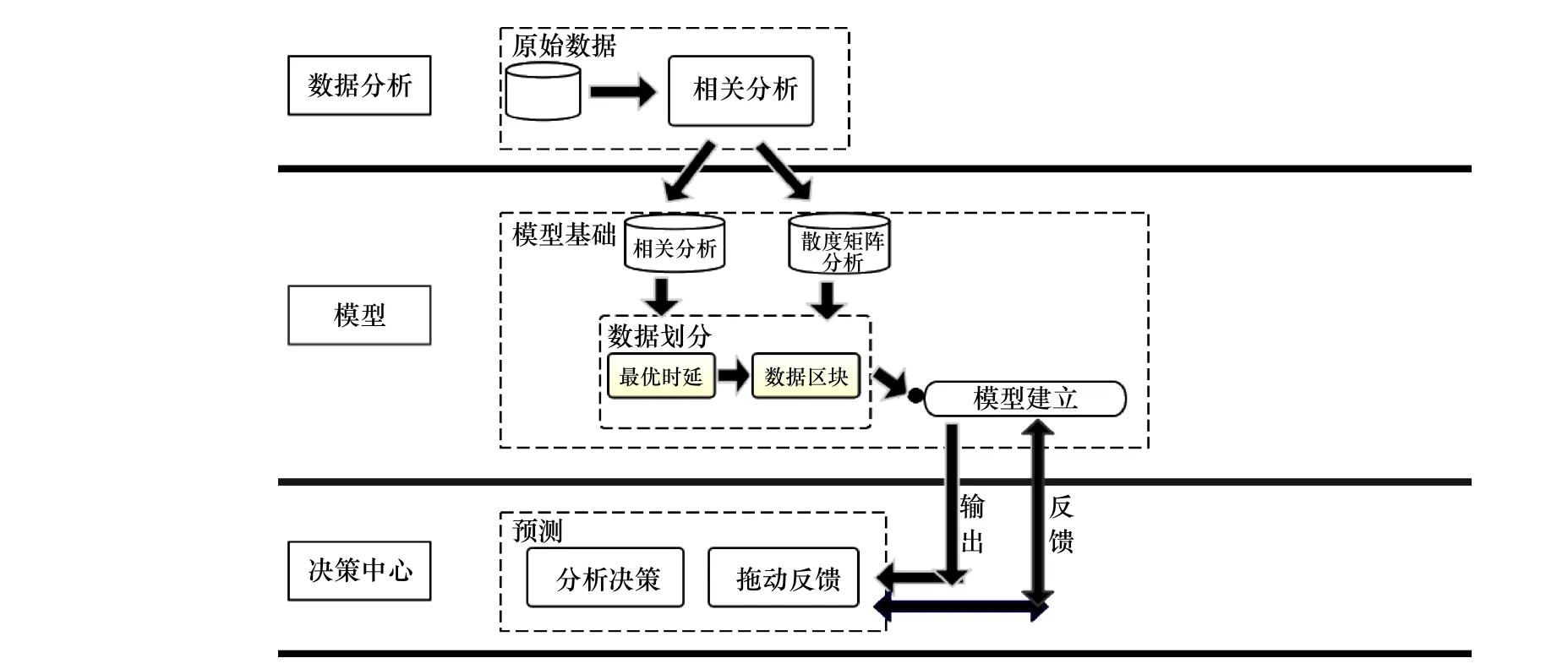
图 2 研究方法图Fig. 2 Research method map

本文对不同海洋要素间关系采用相关系数方法计算出不同时间延迟下的相关系数大小，确定最优时间间隔，相同时间间隔的作为一个整体划分。对于叶绿素a 要素与其他任意一个要素的时间序列定义为yi分别为 Xi在 X 中的排行以及 Yi在 Y中的排行。将集合x 、 y中 的元素对应相减得到一个排行差分集合d，其中di=xi−yi， 1 ≤i ≤N 。随机变量 X 、 Y之间的斯皮尔曼等级相关系数可以由x 、 y或 者 d计算得到，其计算方式如下所示

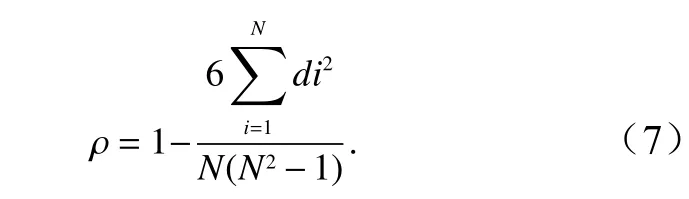
相关关系是一种非确定性的关系，相关系数是研究变量之间线性相关程度的量。我们将相关系数定义为：

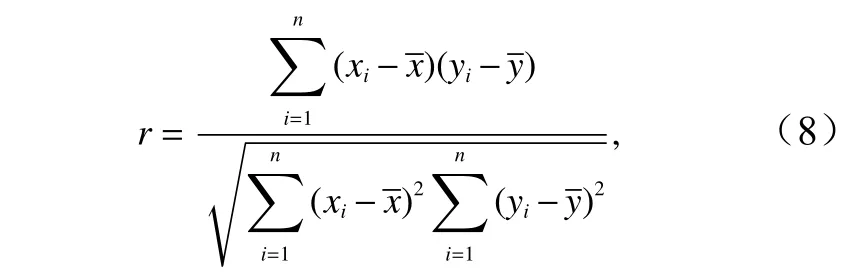
4.3 LSTM 神经元

LSTM 由Hochreiter 和 Schmidhuber(1997)提出[15–16]，随后Alex Graves 对算法进行了改良和推广[17]，基于改进的LSTM 相关网络结构得到了广泛的应用。例如，文献[18]将降雨量的预报作为一个时空序列预报问题，应用LSTM 结合CNN 来预测一个地区在相对较短时间内的未来降雨强度；文献[19]将海水海表面温度（Sea Surface Temperature, SST）预测作为一个序列预测问题，建立了一个端到端可训练的LSTM 神经网络模型，从时空角度利用历史数据预测未来的SST 值，各像素的局部相关性和整体性可以通过固定尺寸的板块来表达和保持。LSTM 通过遗忘门和输出激活功能的设计来处理信息的长短期记忆，其神经元结构如图3 所示，它包含一个动态的门机制，由输入门、输出门、遗忘门和记忆单元组成[20–22]。

图4 详细的描述了LSTM 内部的数据流，其中遗忘门读取上一个状态 h _(t −1) 和 当前输入状态 x_t的信息，通过 S igmoid层输出一个在0 到1 之间的数值给每个细胞状态 C_(t −1)，C _(t −1)中的数字决定从细胞状态中丢弃什么信息，1 代表“完全保留”，0 代表“完全舍弃”。我们通过输入层来决定什么样的新信息将被更新并且放在细胞状态中，首先将 h_(t −1) 与 x_t输入Sigmoid 函数确定将要更新的值，然后通过 t anh 层创建候选值向量随后将旧状态与 ft相乘，确定我们需要遗忘的信息，加上与的乘积产生新的候选值，最终我们根据新的细胞状态来决定输出什么值，通过Sigmoid 层决定输出的细胞状态，将细胞状态通过tanh层进行处理并将其与 Sigmoid的输出相乘得到这一时间的输出，可以形式化的描述如下：

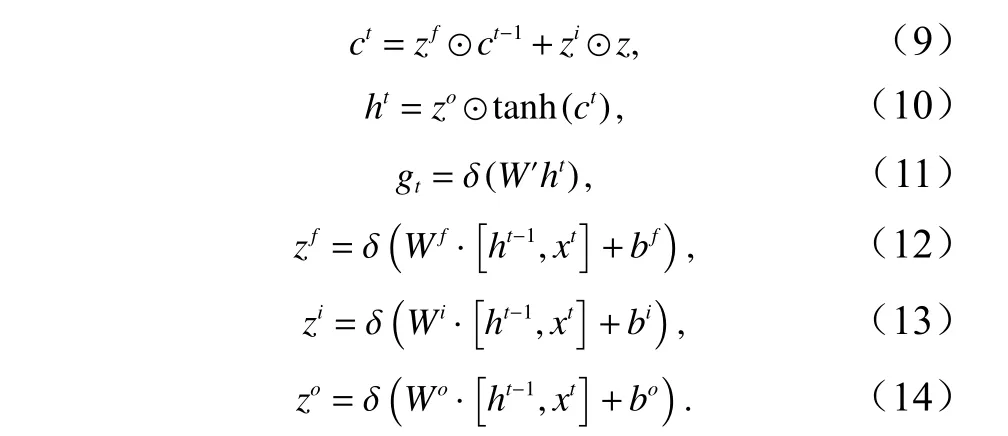
4.4 Merged-LSTM 时间序列学习结构

根据前面数据分析结果构建融合的LSTM 时间序列学习模型，模型结构如图5 所示。模型的输入数据分为两类，其中第一类是根据4.2 节长短期依赖时间分析方法得到的短期依赖要素，标记为OS，即在5 d 内相关系数相似的因素类，另一类是根据长短期依赖时间分析方法得到的长期依赖要素，记为BS，即在5 d 到15 d 时间内相关系数相似的因素类。如图5所示，从模型的第二层开始，我们分别对BS 和OS 两类不同的依赖关系要素采用不同的结构进行训练，其中一个用于训练OS 序列，使用一层的LSTM 来进行短期依赖记忆；另一个用于专门训练BS 的时序依赖关系，使用两层的LSTM 来进行长期依赖记忆，之后使用一层Merge Layer 将两类经过LSTM 训练之后的数据合并起来，最后将输出数据送入Rectified Linear Units 进行激活，以便达到更快的收敛速度，最后通过输出层Linear 线性输出[23]得到最终预测结果。

图 3 LSTM 神经元结构Fig. 3 Neuron Structure of LSTM

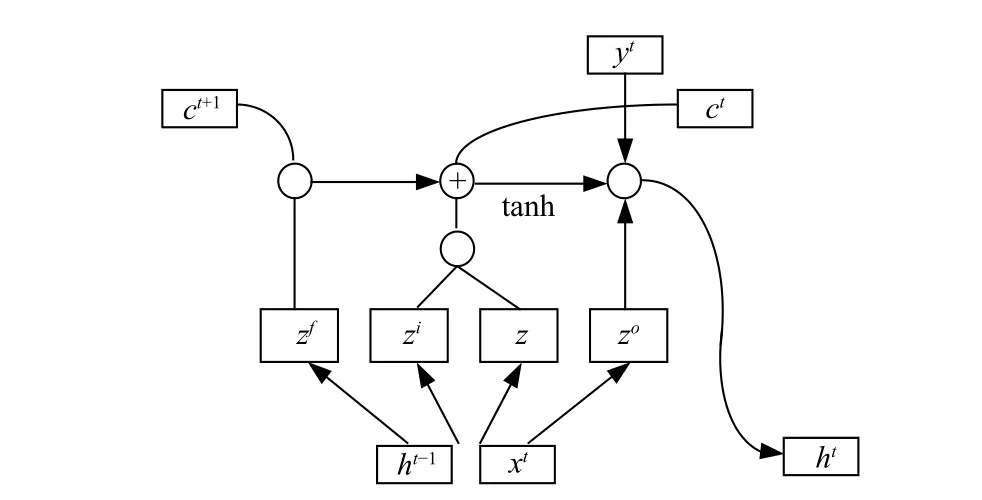
图 4 LSTM 内部计算流程图Fig. 4 LSTM internal calculation flow chart

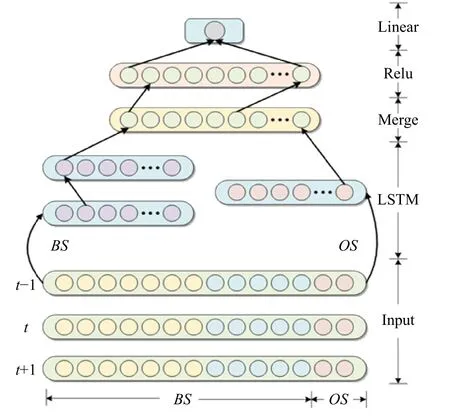
图 5 Merged-LSTM 结构图Fig. 5 The structure of Merged-LSTM

网络采用如下交叉熵公式：

其中 y 是我们预测的分布， y′是真实的分布，交叉熵作为指标来衡量模型的预测用于描述真相的好坏，在这里我们通过梯度下降方法最小化交叉熵来使模型的输出更符合真实分布。

5 实验结果与分析

本文采用2.1 节的数据源去除无效数据，然后对数据进行归一化和自相关性分析，然后利用多要素间关联分析方法得到要素之间的关联关系如图6 所示。

图 6 要素间相似矩阵图Fig. 6 Similarity matrix diagram between elements

图6 的每一个小图都表示任意两个要素之间的相关程度，其中对角线所示的子图为每个要素的自相关曲线，我们可以观察叶绿素a 与其他各要素之间的关系。从图中可以看到，叶绿素a 与其他要素间的相关散布矩阵多呈现有规则的点云形状，形状越规则，相关性越强。从分析结果可以看出各个属性与叶绿素a 之间都存在一定的相关性，因此本文选取全部8 个要素作为预测叶绿素a 浓度的基础数据。

根据选取的所有要素，利用长短期依赖时间分析法计算出其他要素与叶绿素a 浓度在不同时延下的相关系数，见表1 所示。

表1 为叶绿素a 浓度与各个要素在不同时延下的相关系数，每一列代表5 个数据的时延关系，根据计算出的相关系数，我们可以把采集到的不同维度进行分类，在本文中把相关系数绝对值0.2 以下的定义为短期依赖关系，0.2 以上的定义为长期依赖关系，这样可以把这8 个要素划分为两类，一类是与叶绿素a 浓度具有长期依赖关系，另一类与叶绿素a 浓度具有短期依赖关系。不同的依赖关系分别用不同的神经网络单元及层数训练，然后在融合层进行信息融合，为模型建立提供依据。

本文模型中OS 子网络中，每个隐藏层LSTM 神经元个数设置为64，BS 子网络中，每个隐藏层LSTM神经元个数设置为128，参数利用随机正态分布进行初始化，初始学习率设置为0.01，学习率按照lrt=lr0/(1+kt)进行递减，其中 k为控制减缓幅度， t 为训练次数，本文中 k 设置为0.005。训练集数据为样本数据的70%，验证数据集为样本数据的30%，由图7 可知误差下降速度较快，在训练次数为300 次时基本达到收敛，并且在下降过程中没有出现剧烈的抖动，表明本文所提出的模型结构具有收敛速度快和训练稳定性高的优点。

我们对比了本文所提出的模型与传统的多元线性回归(Regression)，多层感知器(Multi-layer Perceptron, MLP)以及递归神经网络(Recursive Neural Network, RNN)对叶绿素a 浓度的预测结果，图8 为实验对比分析图，其中横坐标为时间点的个数，共30 个时间点，每个时间点相差5 min，纵坐标为归一化后的叶绿素a 浓度值。图9 为实际叶绿素a 浓度值和预测叶绿素a 浓度值的真实误差对比，从图中可以看出这组实验在预测误差方面本文方法比以上所提的4 种方法低很多。

我们通过计算不同方法的平均误差发现，本文所提出的模型在实验中误差结果别为0.11，取得了最好的结果。传统的多元线性回归的误差结果为0.48，优于多层感知器模型MLP 的误差结果0.49，递归神经网络的误差结果0.16，优于传统的多元线性回归的平均误差结果。综合以上分析，我们发现考虑不同要素在不同时间点之间的内部关系，对叶绿素a 浓度的预测结果准确性可以得到大幅度的提升，其次由于递归神经网络将要素间的长短期依赖关系看做相同的整体，因此其预测误差比本文所提出的模型大。同样的，这也表明我们不能简单的将多要素的信息看做一个整体，而是需要先对各要素间的长短期依赖关系进行分析，再依据分析结果设计合理的网络结构。

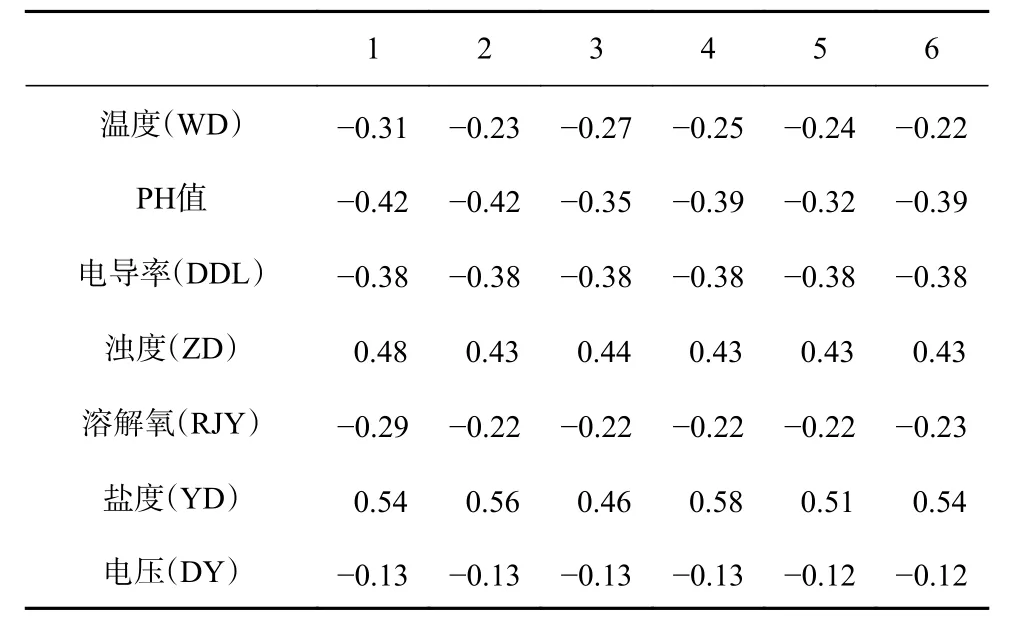
表 1 不同时延下相关系数Table 1 Correlation coefficient under different time delays

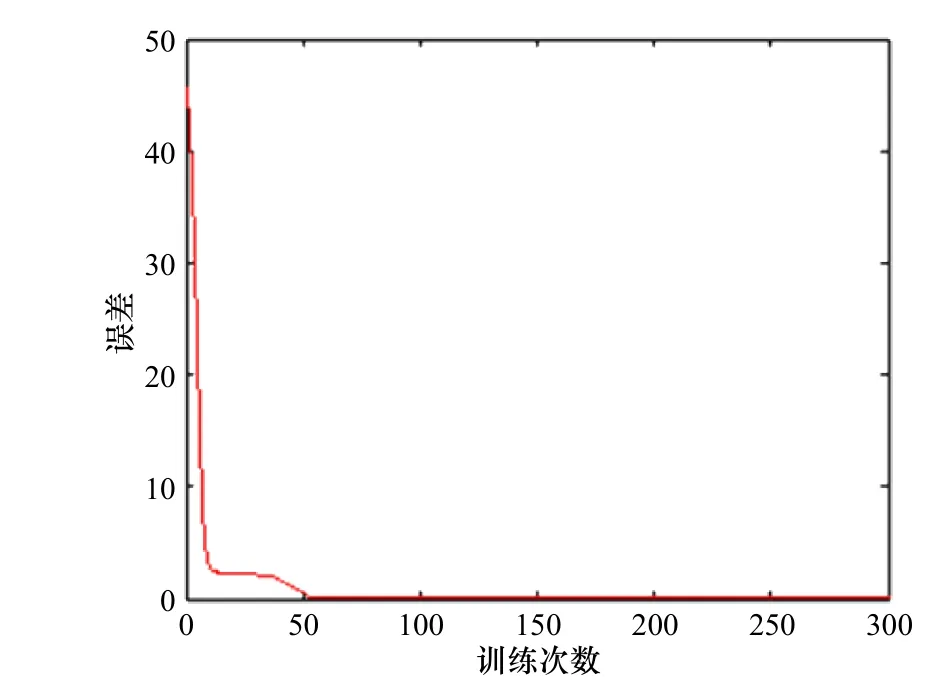
图 7 模型训练误差下降情况Fig. 7 Decline of model training error

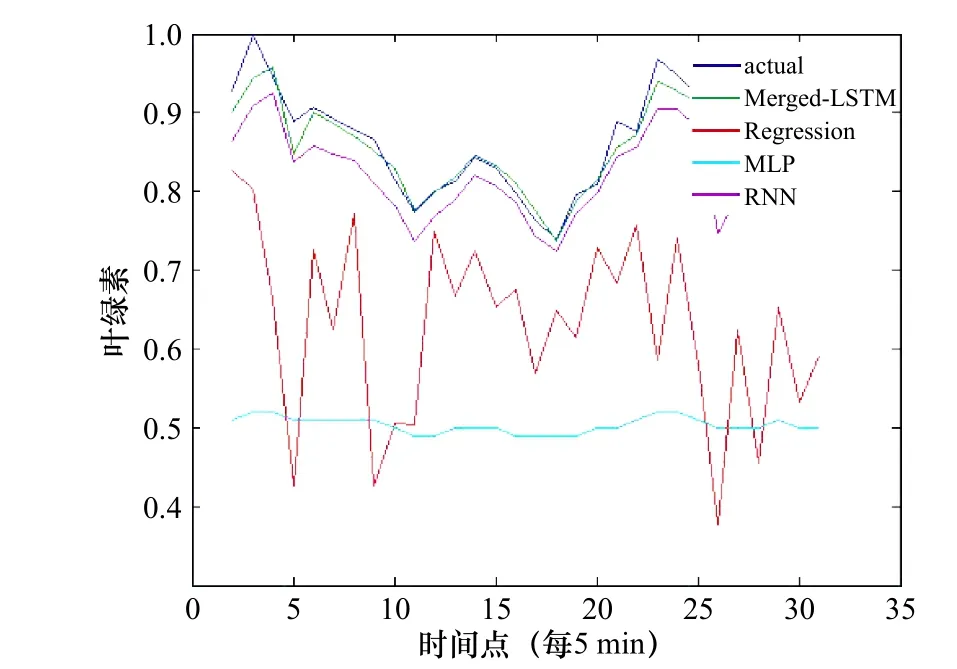
图 8 实际叶绿素a 浓度值和预测叶绿素a 浓度值Fig. 8 Actual and predicted chlorophyll a concentration

6 结论

本文考虑到多要素与叶绿素a 浓度之间的关联性，再加上多要素与叶绿素a 浓度的长短期依赖关系，并结合长短期记忆的人工神经网络预测叶绿素a 浓度取得了较高的预测精度。

（1）本文分析了与叶绿素a 浓度相关要素的长短期依赖关系，发现在不同的时间点，各要素间依据相关系数可以分为两种依赖关系，从查询文献中发现，本文作为第一次提出对于原始要素的分析研究。

（2）本文依据要素间不同的依赖关系所得的分类结果，我们将原始输入要素分为两个不同的子网络进行训练，不同的子网络所采用的神经元和激活函数不同，最后在融合层进行特征的融合，该网络结构具有一定创新性。本文所提出的网络模型结构与Regression、MLP、RNN 在叶绿素a 浓度的预测结果中，本文的模型误差均有大幅度的下降（图8，图9）。

（3）本文所提出的模型具有收敛速度快，训练过程平稳的特点。从图7 中可以发现，本文所提模型结构训练误差下降较快，在300 步后，误差趋于收敛状态，其次我们发现误差下降过程平稳，没有出现剧烈的抖动情况，这一现象说明了模型在收敛速度及训练过程中的优点，另一方面也证明了本文所提模型的可行性。

图 9 实验结果图Fig. 9 Experimental results