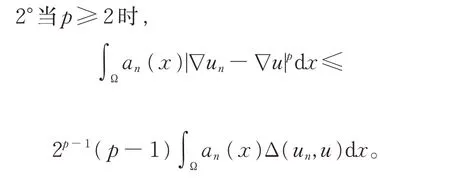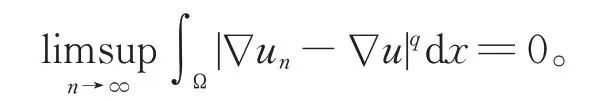一个带权函数的拟线性椭圆方程的有界弱解
李仲庆
(贵州财经大学数统学院,贵州贵阳550025)
1 问题介绍
设Ω是RN中的有界开集,其光滑边界记为∂Ω。研究以下拟线性椭圆方程

其中,1 (H1)a(x)是一非负的可测函数,a(x)∈Lr(Ω),r>1;且 (H2)函数f(x)∈Lm1(Ω),F(x)是一个向量场,并且 |F(x)|∈Lm2(Ω),其中, 当a(x)≡1时,问题(1)就是来源于流体力学的p-Laplace 方程。这种不带权函数方程的有界弱解的结果可参见文献[1]。关于主部退化强制方程的研究见文献[2]。CIRMI 等[3]研究了带权形式的具自然增长条件的椭圆和抛物方程,使用的主要工具为带权的Sobolev空间及带权的Sobolev 嵌入[4]。DRÁBEK 等[5]研究了带权Sobolev空间框架下的pseudo-monotone算子理论。 本文的主要特点是不需要、也不涉及复杂的带权的Sobolev空间,也不使用复杂的带权形式的Sobolev 嵌入,而是在经典的Sobolev空间中去研究带权函数的椭圆方程,使得对问题的研究更加简单和基础。 主要技术路线:合理处理主部扩散项中的权函数,采用改进的De Giorgi 迭代技术,得到L∞估计。应用合适的检验函数于正则化方程,得到梯度序列的几乎处处收敛和解的存在性。 主要结果如下: 定理1假设(H1)、(H2)成立,那么问题(1)存在有界弱解u∈W1,q0(Ω)∩L∞(Ω)。其中,u为分布意义下的弱解,对任意的ϕ∈C∞0(Ω),有 上述结果可分几部分来证明。 受文献[6]启发,给出问题(1)对应的一个正则化方程: 其中, 这样就有an(x)≤a(x)+1;an(x)→a(x),a.e.于Ω,且 由pseudo-monotone算子理论[7],对每一个固定的正整数n,正则化问题 (2)存在弱解 引理1如果条件(H1)、(H2)成立,那么问题(2)的弱解序列{un}∞n=1是本征一致有界的,即存在不依赖于n的正常数C,使得 证明记Gk(s)=(|s|-k)+sign(s),选取Gk(un)作为问题(2)的一个检验函数,得到 1o记Ak={x∈Ω:|un(x)|>k},|Ak|表示集合Ak的Lebesgue 测度。由Hölder不等式和Sobolev 嵌入(记SN,q为嵌入常数对式(4)右端两项分别做估计: 2o注意到由Hölder不等式、q 这样,根据 式(3),(5),(6)和带ε的Young不等式,可得 3°根据Sobolev 嵌入 对上式估计, 其中,C仅依赖于初始数据N,p,s, 4°对任何的h>k>0,有 因此,由式(7)和(8)得 其中 注意到q的定义,则有 由改进的De Giorgi 迭代引理[8],对所有的正整数n和几乎处处的x∈Ω,有|un(x)|≤C,其中正常数C不依赖于n。 选取un作为问题(2)的一个检验函数,得到 式(9)用到了un的一致L∞有界和Hölder不等式, 应用Hölder不等式、带ε的Young不等式、式(3)以及式(9),有 于是上式可估计为 注意到(H2)以及1 即q′ 根据紧嵌入定理可得 由于所研究的问题是拟线性的,所以式(12)并不能保证正则化问题的极限过程。这是因为弱收敛无法保持非线性[9],需要证明关于梯度序列进一步的收敛性。 选取un-u作为问题(2)的检验函数,可得 由式(12)和(14),有 其中, 受文献[10]启发,证明式(15)蕴含 1°当1 由式(15),(12),(9)以及ε的任意性,得到式(16)。 由式(15)直接可得式(16)。 根据式(16)以及 可得 最后,选取ϕ∈C∞0(Ω)作为问题(2)的一个检验函数,应用Vitali 定理和弱收敛的定义,取极限即得到u是问题(1)的一个有界弱解。


2 正则化问题
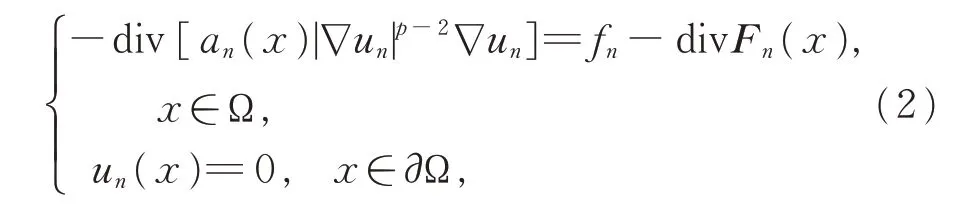

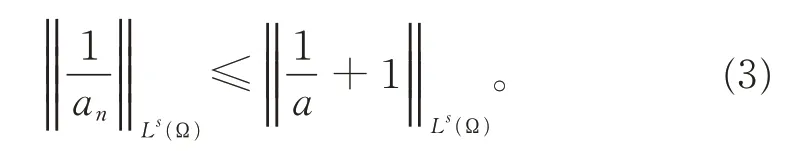
3 最大模估计



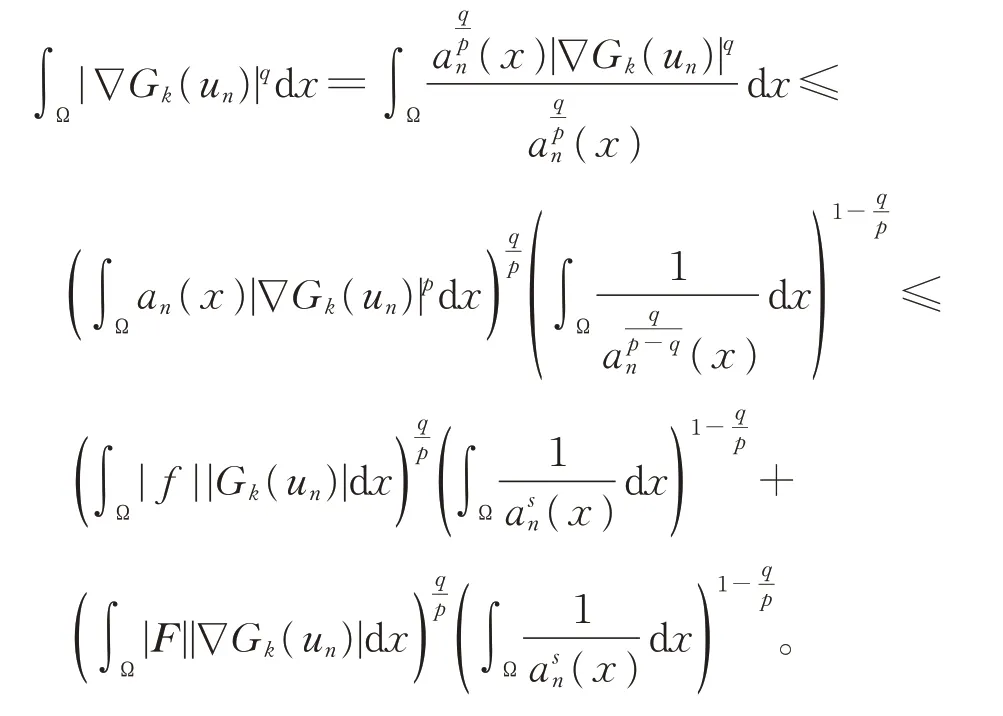






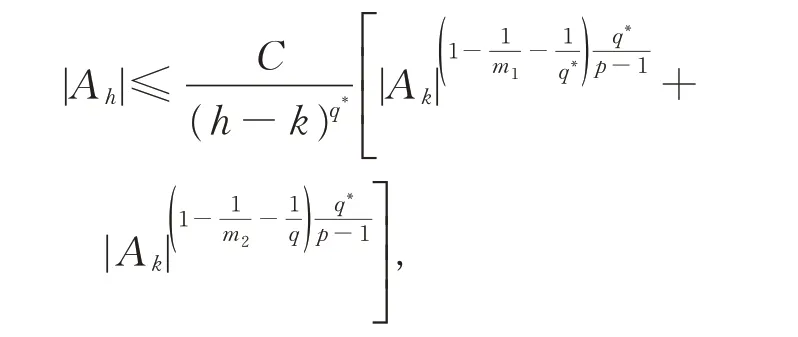


4 弱解的存在性
4.1 un的几乎处处收敛

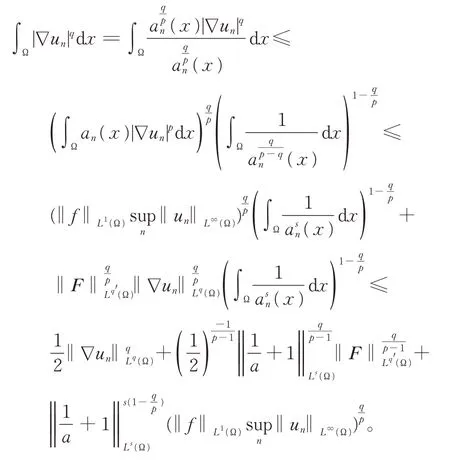
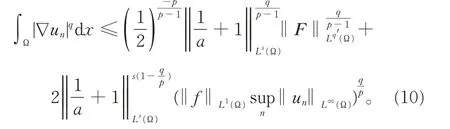




4.2 ∇un的几乎处处收敛