风电场湍流强度对机组结构疲劳安全性的研究

(中车株洲电力机车研究所有限公司，株洲 412000 )

0 引 言

特定风电场机组结构疲劳适用性评估影响最大的因素为风电场的湍流强度[1-3]，而机位点湍流强度受地形、地表粗糙度、测风数据的质量、测风塔塔影风资源评估软件的准确性的影响，都会对扇区的湍流强度造成潜在的畸变，但缺乏量化的评估方法和标准。

IEC61400-1标准对风电场机位点的湍流强度适用性采用等价湍流强度对结构的安全性进行评估[4]，但风电机组结构部件采用的材料种类较多，在适用性评估中，需根据不同材料的Wöhler指数m[5]得到等价的湍流强度，进行载荷迭代计算，依据迭代后的载荷进行等效疲劳载荷的对比进行适用性分析，迭代过程相当繁琐存在较大的局限性。

文中提出基于扇区权重的k阶原点和中心矩算法[6-8]对湍流强度不确定度的计算，并对湍流强度的不确定度进行了定义，可以快速的评估机位点的扇区湍流强度是否存在畸变，并为复杂地形条件下机位点的扇区控制提供计算依据。

针对等价有效湍流强度进行特定场址结构安全性评估的方法局限性进行了推广和优化，基于包络定理[9]构建轮毂高度处扇区的最大参考湍流强度函数求解扇区的最大湍流强度包络线，并依据各扇区的湍流强度包络线和发生的频次对机组结构部件的安全性进行评估的方法，可以快速的根据各扇区的有效湍流强度对结构的安全性进行评估。

1 等价湍流强度理论基础

传统特定风电场机位有效湍流对结构安全性评估主要分为两个部分，为安全性判断标准和等价有效湍流强度Ieff的求取。

1.1 特定机位点湍流强度安全性判断标准

(1)

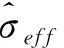
σ1=Iref(0.75Vhub+b);b=5.6 m/s

(2)

式中，Iref为参考湍流强度。

1.2 等价有效湍流强度Ieff的计算

对于规则排布及非规则排布的风场，使用等价有效湍流强度Ieff来等价临近机组产生的尾流效应对机组疲劳载荷造成影响的结果。

(3)

上式等效为：

(4)

式中，P为风向分布的概率密度函数；I为θ方向有效湍流强度；m为材料的Wöhler指数。

对于风向均匀分布且风场为规则排布的矩形的风电场。其尾流可按如下公式进行计算。

若min{di}≥10D：

(5)

若min{di}<10D：

(6)

其中：

pw=0.06

式中，令m=2，可得到简化的Frandsen模型，如下所示：

(7)

(8)

(9)

(10)

2 扇区有效湍流不确定度检验

2.1 基于权重的k阶原点和中心矩算法

原点矩定义[10]：设一随机变量x，若E[xk]存在，则称E[xk]为x的k阶原点矩，简称k阶矩(其中k=1,2,…)。

中心矩定义[10]：设一随机变量x，若{[x-E(x)]k}存在，则称{[x-E(x)]k}为x的k阶中心矩(其中k=1,2,…))。当k=1时，均值E(x)为随机变量x的一阶原点矩，方差D(x)=[x-E(x)]2为随机变量x的二阶中心矩。

由于检验湍流异常与其在扇区的发生频次(权重)密切相关，这里构建基于扇区权重的k阶原点和中心矩的算法[11-12]对扇区湍流强度的异常值进行检验。

设一随机变量x，在扇区i发生的频次(权重)为Pi，可以构建基于权重的k阶中心矩的函数如下：

2.2 构建扇区的k阶原点和中心矩函数并求解

根据公式(11)求得所有扇区基于权重的k阶中心矩之和。假设特定场址划分为N各扇区、每个扇区风速发生的频次(权重)Pi的总的k阶中心矩之和的函数关系可以改写为：

d(Ieff-i,E(Ieff-i))=

(12)

式中，E(Ieff-i)可以定义为基于权重的各扇区有效湍流强度Ieff-i而等价的所有扇区的等价湍流强度Ieff，为基于权重的k阶原点矩，其表达式如下：

(13)

由于(m,k∈R)，可以将材料Wöhler指数m和k阶中心矩的k值进行替换。将公式(13)带入公式(12)，得到：

(14)

根据公式(14)求各扇区的有效湍流Ieff-i和所有扇区的等价湍流Ieff在材料Wöhler指数m阶下的中心矩。其含义为：中心矩越大,代表各扇区之间的有效湍流偏差大，中心距越小，代表各扇区之间的有效湍流偏差越小。

2.3 有效湍流强度异常度等级划分

根据扇区的基于权重的k阶中心矩检验风电场各扇区的有效湍流强度是否异常。根据异常度的计算结果，并结合参考湍流等级的分类(划分为A、B和C三类，分别对应0.16、0.14和0.12的参考湍流强度，每个等级间参考湍流强度间隔0.02)[1]，将机位点各扇区的有效湍流强度异常度划分为三个级别，见表1。

表1 机位点各扇区有效湍流强度异常度等级划分

通过m阶下的中心矩求解，结合风电场场址地形可以排除测风数据的异常导致等价湍流Ieff失真的问题，同时对于复杂地形风电场的特定扇区管理控制提供了设计依据，从而提高风电机组在复杂地形条件下的适应性和降低机组的综合成本。

案例：某风电场扇区有效湍流异常湍流值检验计算过程。表2数据为某一平坦地形的测风塔一年的测风数据，并根据该测风数据求得的该扇区的有效湍流值。

表2某风电场各扇区有效湍流强度值及其权重

注：Ieff-i为某一机位点各扇区的正常有效湍流值，Ieff-i′为扇区13的数据由于该扇区测风仪在测风塔的气流下方，导致塔影效应，其有效湍流产生畸变。

根据公式(13)，当材料Wöhler指数m为10时，计算可以求得：

Ieff=0.135，d(Ieff-i,Ieff)=0.012；

Ieff′=0.145，d(Ieff-i,Ieff)′=0.027；

根据基于权重的中心矩计算，可以判断出该机位点的测风数据的有效湍流的异常度，通常可以根据异常度的等级划分进行机位点测试塔测风数据的排查；针对复杂地形，可以根据基于权重的中心矩计算，确定风电场需要进行扇区管理控制的机位点，并根据有效湍流强度异常度划分机组的可靠性等级进行分级管理。

3 改进的场址有效湍流评估方法

3.1 分扇区划分计算定义

将场址的风向分布平均划分为多个扇区，分别命名为扇区1、扇区2……和扇区[13]。

定义扇区1对应的有效湍流为Ieff-1，扇区2对应有效湍流为Ieff-2，以此类推扇区N的有效湍流为Ieff-N；扇区1的风向分布概率为P1，扇区2的风向分布概率为P2，以此类推扇区N的风向分布概率为PN。则各扇区的有效湍流根据公式表达为：

(15)

式中，Ieff-i为扇区i的有效湍流强度；Iamb-i为扇区i的环境湍流强度；ΔIadd-i为扇区i尾流引起的湍流强度。

3.2 扇区最大包络函数

根据包络定理：定义扇区的最大包络参考湍流强度函数为：

(16)

式中，Vhub为轮毂高度处风速，为给定的轮毂高度处风速离散参数；Ieff-i为扇区i轮毂高度处风速下对应的随机变量的有效湍流强度，为目标函数中的选择变量；Ieff-i为轮毂高度处风速Vhub和有效湍流强度Ieff-i(Vhub)对应的参考湍流强度函数。

(17)

上式两边，对参数Vhub求导，可以得到：

式中，“[ ]”右边的下标“Vhub”表示对参数Vhub的求导，上标“*”表示求导后的结果在最优解处的取值。由于是最优解处的取值，故由一阶必要条件可知Ieff-iIeff-i=0，得到[Iref-iVhub]*，表示原目标函数Ieff-i(Ieff-i,Vhub)对Vhub求导后在最优解处的取值。

根据公式(18)求得特定场址风机机位点扇区Ieff-i有效湍流强度φ(Vhub)的最大包络参考湍流强度函数φ(Vhub)。而IEC61400-1标准湍流强度的安全适应性评估只需要验证轮毂高度风速Vhub的有效区间为[Vave,2Vave][1]，公式(18)只需在区间[Vave,2Vave]进行φ(Vhub)的求解。

案例：机位点在轮毂高度风速区间[Vave,2Vave]，扇区i的最大包络参考湍流强度函数φ(Vhub)如图1所示。

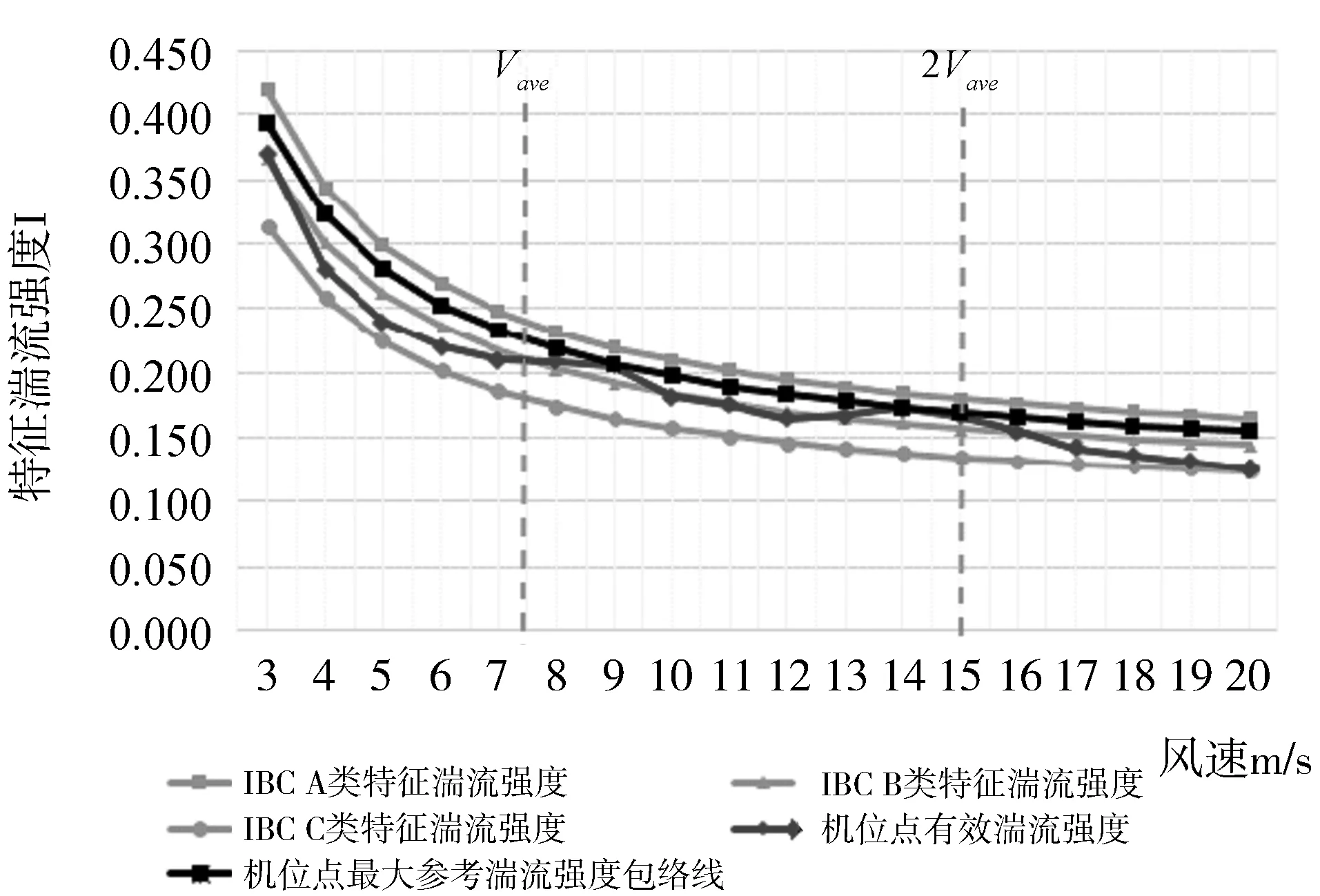
图1 最大包络参考湍流强度函数

3.3 建立等效载荷和有效湍流强度的线性关系

根据文献[14]等效载荷和湍流强度有如下关系：

e(U,θ)≈ασuσu+αττ+αwτw+αff

(19)

g((σu,τ,τw,f|U,θ))dσudτdτwdf

(20)

αττ+αwτw+αff≈常数

(21)

式中，U为平均风速；θ为风向；e(U,θ)为线性等效载荷；σu=σu(U,θ)为风速波动标准偏差；τ=τ(U,θ)为气流垂直方向平均剪切；τw=τw(U,θ)为尾流引起的平均流速差；f=f(U,θ)为湍流频率范围；g((σu,τ,τw,f|U,θ))为由于Wöhler指数m积分导致等效载荷上升的修正系数。

加强野外火源管理。防火期内，各级森林防火指挥中心安排专人值守，74个视频监控点全部开通，实行24小时自动巡航，发现火源自动报警；98座了望台安排双人双岗，不间断观测林区火情；进山路口安排防火检查站，宣传防火知识，严防火种进山；全市2300名护林员上岗到位，加强野外火源巡查；各级森林公安机关及时查处森林火灾案件，坚决打击野外违法用火行为。

由以上可以得到：

Iref-i∝Ieff-i∝Fequ-i

(22)

令：

Ieff-i=α·Fequ-i

(23)

则有效湍流强度Ieff-i和等效载荷Fequ-total的转化关系如下：

(24)

式中，α为等效载荷和自定义参考湍流强度的线性比例因子；Fequ-i为扇区i的等效疲劳载荷；Fequ-total为所有扇区的等效疲劳载荷。

3.4 等效疲劳载荷计算

扇区i根据湍流强度Ieff-i计算得到所有工况下等效到20年(等效到1×107次数下)，则扇区i的等效疲劳载荷和其对应工况关系表述为：

(25)

式中，i为扇区编号(i=1、2、3、…、N)；为工况编号(j=1、2、3、…、n)；Fi-j为每个工况等效到20年下对应的等效疲劳载荷。

扇区i根据湍流强度Ieff-i计算得到的全套载荷等效到不同材料Wöhler指数m下的等效疲劳载荷示意见表4所示。

所有扇区的等效疲劳载荷计算根据各扇区的风向分布Pi和各扇区的等效疲劳载荷Fequ-i以及材料Wöhler指数m等效综合得到，其公式为：

表3等效疲劳载荷示意表

(26)

(27)

综上对不同材料Wöhler指数m下等效载荷Fequ-total与标准机组设计等效疲劳载荷进行归一化比较，则可对特定场址湍流强度对机组结构疲劳的安全性进行验证。

4 结束语

文中构建了基于扇区权重的k阶原点和中心矩算法对湍流强度不确定度的计算方法，并对湍流强度的不确定度进行了等级划分，该方法可以快速的评估机位点的扇区湍流强度是否存在畸变和为复杂地形条件下，湍流强度不确定高的机位点进行扇区管理控制提供理论计算依据，并可以以湍流强度的不确定度对机组的可靠性进行分级管理。

文中基于包络曲线构建的最大参考湍流强度函数以及扇区有效湍流和等效疲劳载荷的转化求解方法，是对既有的基于等价湍流强度进行结构疲劳安全性评估的扩展和优化，弥补等价有效湍流强度评估结构部件安全性需要根据不同材料Wöhler指数m不断迭代进行载荷计算的缺陷，具有较好的工程应用价值。