能量采集技术在主动窃听系统中的应用研究

方毓恺，贺玉成,2，周 林,2

(1.华侨大学 厦门市移动多媒体通信重点实验室，福建 厦门 361021；2.西安电子科技大学 综合业务网理论及关键技术国家重点实验室，陕西 西安 710071)

0 引言

在传统的保密通信中，信息的加密主要依赖于上层协议中的数据流加密，这项技术虽然能够有效提高信息传输的安全性，但是密钥管理往往伴随着计算上的高复杂度[1]、高成本以及传输时延的增加等一系列问题。近年来物理层安全技术得到了研究学者们的广泛关注，该技术利用信道传输的动态特性，从物理层低层协议上确保了信息传输的安全性[2]。

在传统的物理层安全技术研究中，合法通信系统考虑采用协作中继[3]、多输入多输出(Multiple-Input Multiple-Out,MIMO)[4]等技术来提高自身的安全性能。在此基础上，文献[5]还分析了放大转发协议(Amplify and Forward,AF)和译码转发协议(Decode and Forward,DF)下的最优中继选择策略，证明了在该策略下能够有效阻止窃听用户窃听中继转发的信号。针对大规模MIMO下的系统保密性能，文献[6]推导并验证了天线数量是影响MIMO系统通信安全性能的重要因素。值得指出的是，在另一方面这些技术也可能被不法分子用来进行犯罪活动，如利用无人机窃取商业军事机密等，于是有必要对这些活动进行合法的监管，也称之为主动窃听[7]。

对于主动窃听系统，窃听者在窃听的同时也进行干扰。因此为了提高窃听速率[8]，在干扰和窃听之间的模式选择也是重点研究的对象[9]。在单窃听用户的基础上，研究学者还考虑增加窃听和干扰用户数量来提高主动窃听性能，如在文献[10-11]中，Jihwan Moon等人通过优化多窃听用户的发送矢量以及干扰机的预编码矩阵，大幅度提升了窃听系统的性能。除以上这些因素会对窃听性能产生影响之外，窃听者自身功耗也是影响其性能的主要因素之一，且随着能量采集技术[12-13]的迅速发展，能量采集技术也可能被用在非法用户的信息传递中，文献[14]中结合该技术提出了无线供能可疑网络下的主动窃听研究，通过优化的方法求出了窃听成功率、平均窃听率、相对窃听率和窃听能量效率这4种性能指标最大化的最优能量传输功率。但是目前关于能量采集结合主动窃听的研究依旧较少，因此本文针对能量采集下的可疑网络主动窃听技术展开研究，分析推导了该情况下主动窃听者的窃听性能。

1 系统模型与传输过程分析

1.1 系统模型

如图1所示，系统由可疑用户包括可疑发送者S和可疑接收者D以及主动窃听用户E组成。可疑用户S和D都只配置单根天线，且工作于半双工模式；主动窃听者E配置有2根天线，分别用于发送和接收，且工作于全双工模式。

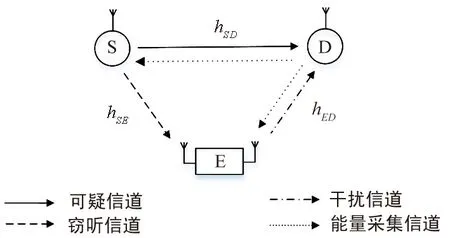
图1 系统模型Fig.1 System model

此外，本文假设由全双工带来的自干扰已通过模拟消除和数字消除技术完全消除。因此，S,D,E之间，E与D之间的信道系数分别表示为hSD,hSE,hED。假设各个信道之间互不相关，并且都服从准静态平坦瑞利衰落，其平均信道功率增益分别为E[|hSD|2]=ΩSD,E[|hSE|2]=ΩSE,E[|hED|2]=ΩED。

除此之外，在此场景下本文假设E对所有信道的信道状态信息(Channel State Information,CSI)都完全已知，这种假设是合理的，因为E离可疑用户较远，所以可疑用户很难发现窃听存在，并且可以通过文献[14]中所提到的方法获得各个信道的CSI。

1.2 传输过程分析

在上述模型中，通信过程可总结为“先采集再传输”，即分为2个过程：能量采集过程和信息传输过程。首先，假设一个传输时隙为1，其中能量采集时间用τ0表示，信息传输时间即为τ1=1-τ0，该时间均由可疑用户决定。在传输时隙内，能量采集与信息传输过程先后依次进行。

1.2.1 能量采集

在D对S广播射频信号充能过程中，E同样进行射频能量采集，且都将能量存储在超级电容器中，但是由于超级电容的自放电特性，本文假设采集的能量仅可用于当前时隙，不可用于下一时隙。假设D广播射频信号的功率固定为PD，则S和E采集的能量结合信道的互易性可以表示如下:

ES=φSPD|hSD|2τ0,

(1)

EE=φEPD|hED|2τ0,

(2)

其中,0<φS<1,0<φE<1为能量采集因子，表示S和E的能量采集效率，τ0表示能量采集时间，τ1表示信号传输时间。为了方便起见假设一个时隙的时间表示为1，则τ1=1-τ0。且由于S和E没有除此之外的能量为自身工作供电，故其功率可以表示为：

(3)

(4)

1.2.2 信息传输

能量采集结束之后，可D停止发送能量，S开始向D发送可疑信息，此时E开始窃听并干扰，则此时D和E上的接收信号为：

(5)

(6)

式中，β表示功率分配因子，且0≤β<1，表示用于干扰的功率所占总窃听者功率的比重，剩余功率用作窃听，值得注意的是，β=0表示功率完全用作窃听，不进行干扰，即被动窃听。nD，nE为D、Ek上的零均值加性高斯白噪声(Additive White Gaussian Noise,AWGN)，且噪声功率都为σ2。因此，根据以上可得D和E上的信干噪比(Signal to Interference Noise Ratio,SINR)可以表示如下：

(7)

(8)

2 窃听性能分析

文中，考虑采用窃听不中断概率[8]作为主动窃听系统的性能指标。即只有当窃听链路的信噪比不小于可疑链路的信噪比时，D才能成功解码窃听到的可疑信号，其他情况下窃听者不能解码窃听信号，即窃听中断。因此窃听中断事件可以定义如下：

(9)

式中，采用X=1和X=0分别表示窃听成功和中断，由此可知随机变量X的期望即为窃听不中断概率。

E{X}=P{γE≥γD} 。

(10)

将式(7)、式(8)代入式(10)中并结合能量采集所得S和E处的功率表达式，可将窃听不中断概率表达化简如下：

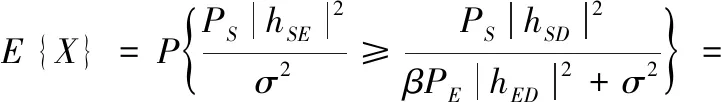
(11)

且由概率论知识可知：

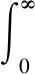
(12)

在此处W为S-E的信道功率增益|hSE|2，其概率密度函数(Probability Density Function,PDF)可表示为：

(13)

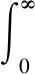
(14)

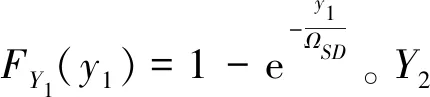
(15)

由此能求出Y的累计分布函数FY(y)，考虑0<β<1(μ>0)和β=0(μ=0)两种情况：

(16)

式中，erfc(·)表示补余误差函数，参照文献[15]中式(7.2.2)。因此结合式(12)、式(13)和式(16)便可得出窃听非中断概率的半闭合表达式：

E{X}=1-ε(2Ci(ν)sin(ν)+cos(ν)(π-Si(ν)))，

(17)

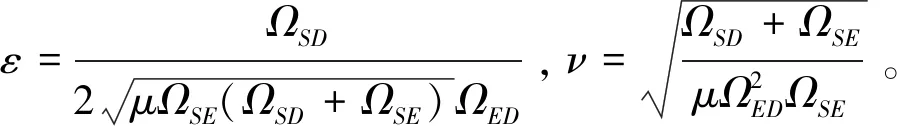
3 仿真结果与分析

针对主动窃听系统中的多窃听用户选择模型在瑞利衰落信道中进行Matlab仿真，对上述理论分析结果进行验证，其中仿真中的相关参数设置如下：噪声功率σ2=0 dBm，可疑用户之间的信道参数ΩSD=1，且为了防止被可疑用户发现，E离可疑用户较远，故其与可疑用户之间的信道为可疑用户之间信道的次级信道，因此设置ΩSE=ΩED=0.2，自干扰信道参数ΩEE=1，蒙特卡洛仿真次数均为100 000次。仿真结果如图2～图6所示。

图2和图3仿真验证了窃听不中断概率与D的发送功率在不同能量采集时间和不同干扰功率分配因子下的关系曲线。图2表明，能量采集时间越长，信号传递的时间越短，并且因为采集到的能量越多，E的总功率越大，因此窃听不中断概率越大。图3表明，窃听不中断概率随着干扰功率分配因子即干扰功率的增大而增大，且随着接收端发射功率的增大，主动窃听明显优于被动窃听(β=0)下的窃听性能。图2和图3都表明可疑接收端的发送功率越大，窃听性能越佳。

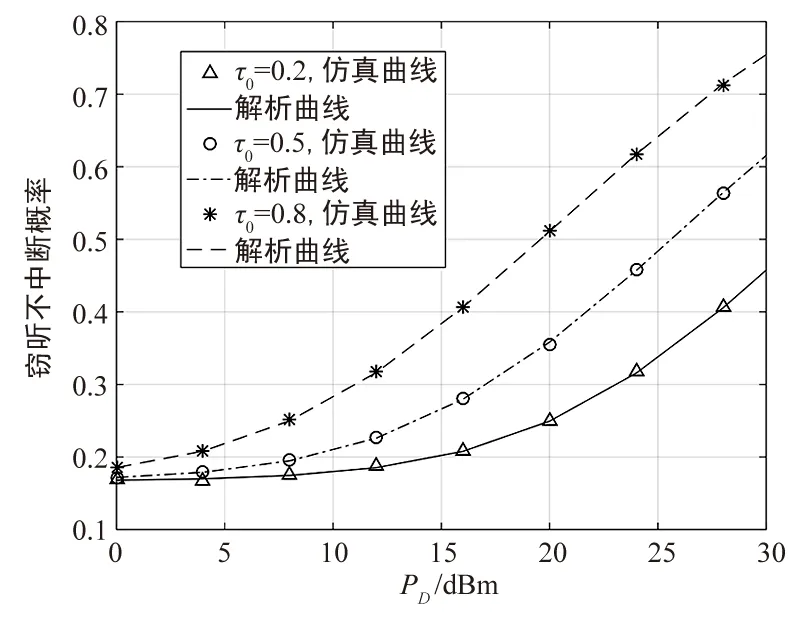
图2 β=0.8，φE=0.6接收端发送功率与 窃听不中断概率的关系Fig.2 β=0.8，φE=0.6 Eavesdropping non-outage probability versus the transmitting power of receiver

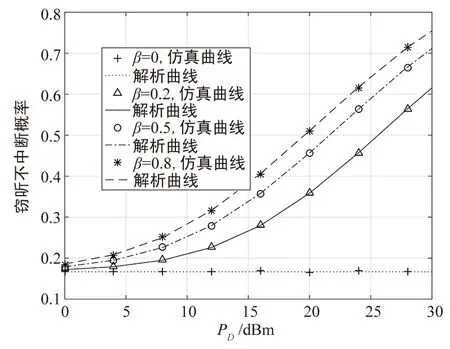
图3 τ0=0.8，φE=0.6接收端发送功率与 窃听不中断概率的关系Fig.3 τ0=0.8，φE=0.6 Eavesdropping non-outage probability versus the transmitting power of receiver

图4和图5仿真验证了窃听不中断概率与能量采集因子在不同能量采集时间和不同干扰功率分配因子下的关系曲线。显然随着能量采集因子即E能量采集效率的增大，窃听不中断概率随之增大，且同图2和图3，随着能量采集时间和干扰功率分配因子增加，窃听性能越好。

图6验证了干扰功率分配因子与窃听不中断概率的关系，观察可以发现，在可疑接收端发射功率与E能量采集效率一定时，随着干扰功率分配因子的增大，窃听不中断概率随之增大。结合以上仿真验证结果我们不难发现，可疑接收端发射功率、E能量采集效率、干扰功率分配因子、能量采集时间都是影响窃听不中断概率的重要因素，且都与其之间存在正比关系。

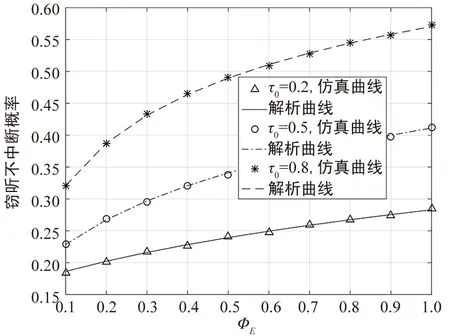
图4 PD=20,β=0.8能量采集因子与 窃听不中断概率的关系Fig.4 PD=20，β=0.8 Eavesdropping non-outage probability versus the energy harvesting factor

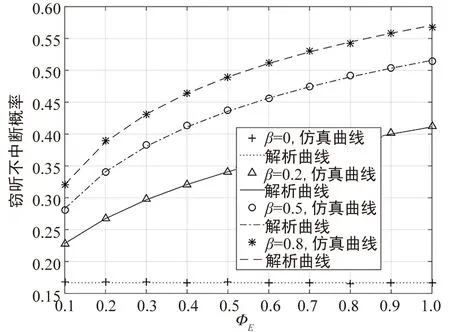
图5 PD=20，τ0=0.8能量采集因子与 窃听不中断概率的关系Fig.5 PD=20，τ0=0.8 Eavesdropping non-outage probability versus the energy harvesting factor

图6 PD=20,φE=0.6干扰功率分配因子与 窃听不中断概率的关系Fig.6 PD=20，φE=0.6 Eavesdropping non-outage probability versus the splitting factor of jamming power

4 结束语

窃听性能的优化，功耗问题在主动窃听系统中一直是影响窃听性能的重要因素，而关于这方面的研究还相对较少。因此本文重点研究了能量采集技术与主动窃听技术结合下的场景应用。计算结果和仿真验证表明：在本文的主动窃听系统中，随着可疑接收端发射功率、干扰功率分配因子、能量采集效率以及能量采集时间的增大，无源E的窃听不中断概率及窃听性能更佳，但是窃听不中断概率与可疑用户的发送功率、能量采集效率无关。除此之外，在与被动窃听方式的性能比较中，主动窃听显然更有优势。