信息论中私密信息检索问题综述

刘 楠，姚昕羽

(1.东南大学 移动通信国家重点实验室，江苏 南京 210096；2.东南大学 信息科学与工程学院，江苏 南京 210096)

0 引言

在这个日益数字化的时代,我们在浏览网页、网上购物、在线社交、导航定位等的同时,越来越多的数字化个人信息流落于网络的各个角落。如何能够保护用户的隐私已成为人们越来越关注的话题。

早在1998年，私密信息检索问题(Private Information Retrieval,PIR)在计算科学领域便受到了广泛的关注。此问题由Chor等人提出[1]：假设一个数据库存有K条相互独立的消息，W1,W2,…,WK，它们的长度都为L。一个用户想通过检索该数据库以获取一条消息的内容。同时，该用户不想自己的隐私被泄漏，即不想让数据库获知具体哪一条信息被检索。因此，用户设计自己向数据库发出的检索请求，以达到下面两个条件：

① 解码条件：根据数据库的回复，用户可以无误地解码自己感兴趣消息的内容；

② 私密条件：数据库从检索请求中，对用户感兴趣消息的下标一无所知。

文献[1]中指出，当只能从一个数据库进行检索时，满足以上两个条件的检索请求只有一种，就是把所有K条消息都进行请求并下载。可见，为了保护自己的隐私，需要付出巨大的下载量浪费。

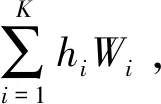
2016年，Sun和Jafar作为信息论研究的学者，对“最优”的检索请求产生了兴趣，他们提出这样一个问题[2]：在所有满足解码条件和单个数据库私密条件的检索请求中，哪种检索请求方式的下载量最小？他们之所以只关心下载量，而不关心检索请求时上传数据量的大小，是因为在信息论中，通常假设消息的长度很长，因此相比于下载量，上传请求的大小可以忽略不计。文献[2]利用信息论的工具完整地解出了私密检索下载量的性能极限，并给出了达到此性能极限的最优检索方法，为人们对私密信息检索问题的理解和方案设计提供了巨大的帮助。自2016年Sun和Jafar文章发布以来，私密信息检索这个原本只在计算机科学领域活跃的研究内容，在信息论领域也备受瞩目，短短几年中已有近100篇该方面的文章。这些论文对各种私密信息检索场景进行了扩展和探究，提出了很多表现优秀的私密检索方案，得出了不少私密检索的性能极限，对现实生活中用户隐私保护提供了大量的理论指导。

本文首先给出传统私密信息检索问题的最小下载量及其证明理论方法。而后，将这几年信息论私密信息检索方面的论文进行归类、阐述与总结。最后，指出私密信息检索方向的未来发展趋势和若干重要开放问题。

1 传统PIR问题

1.1 最小下载量

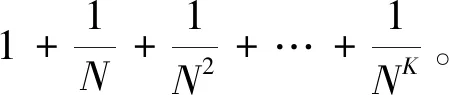
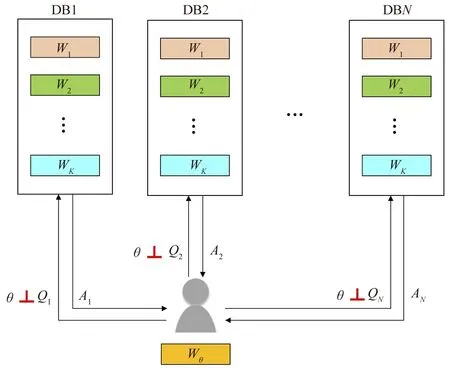
图1 传统私密信息检索问题Fig.1 Classical private information retrieval problem

1.2 最优检索请求

最优的检索请求，即下载总量最少的检索请求，并不唯一[3]。Sun和Jafar在文献[2]中提出的最优检索请求方法，采用了不同消息符号k项求和的形式,k=1,2,…,K。文献[2]的检索请求充分利用了两种对称性：① 消息的对称性；② 数据库的对称性。消息的对称性保证了用户隐私的保密，数据库的对称性可以最大化重复利用那些下载的关于其他非感兴趣消息的数据，这些非感兴趣数据是为保护用户隐私迷惑数据库而下载的。

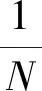
1.3 性能极限

PIR信息论问题的提出和完整解出[2]，引起信息论领域很多学者的极大兴趣。他们开始更深入地探索该问题的其他变种，探求在更灵活、更实际场景中私密信息检索的最优方案。本文将研究方向归为几类进行介绍。

2 第一类变种问题：PIR中其他隐私保护和安全问题

这类问题探索的是PIR中满足其他隐私保护需求和数据安全需求下的最优检索请求方案。具体来说，包括下面几个问题。

2.1 数据库共谋

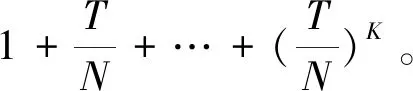
数据库共谋场景下的最优检索方案需要用到MDS码。MDS码可以把重复利用的非感兴趣数据的相关性均匀扩展开来，使得合谋数据库集合由于看到的非感兴趣数据数目不多，感觉不到非感兴趣数据的相关性，进而对于合谋数据库集合来说，非感兴趣数据和感兴趣数据都是不相关的，这样就达到了对隐私的保护。此种场景下的性能极限证明与传统PIR问题证明步骤基本一致，迭代公式的第二步证明需要用到Han′s inequality[5]。在文献[4]结论的基础上，文献[6]将合谋方式的对称性去掉，给出了任意合谋模式下的最小下载量和最优检索请求方案。

2.2 鲁棒私密信息检索

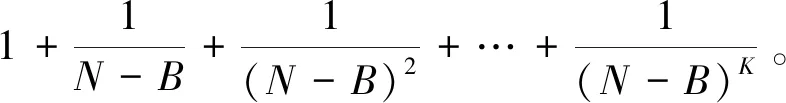
2.3 拜占庭私密信息检索

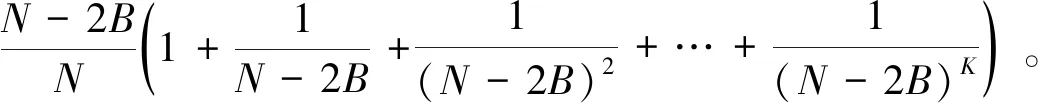
2.4 消息安全

PIR与以往通信安全问题的不同之处在于，它考虑的是消息下标保密，而不是消息内容保密。那么，如果在这类问题中也加入消息内容需对不授权用户进行保密的需求呢？这一类问题中可以进一步按不授权用户的种类进行分类。

2.4.1 对称私密信息检索

2.4.2 外在窃听者

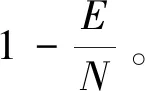
上面介绍的几种扩展都已求得最优检索方案和对应的最小下载量。因此，人们还探索了它们的组合问题，例如鲁棒加数据库共谋[4]、拜占庭加数据库共谋[7]、拜占庭加对称PIR[11]、外在窃听者加数据库共谋[10]以及对称PIR加数据库共谋加拜占庭[12]等。第一类变种问题的共同特点就是最优检索方案和对应的最小下载量基本全部可以完整解出。因此，人们对这一类的问题有着深刻透彻的理解。

3 第二类变种问题：数据库存储空间受限

传统PIR中，假设每个数据库都完整地存有K个消息。这对数据库的存储空间要求很高。因此，人们开始研究数据库存储空间受限情况。第二类变种问题中又分以下4类。

3.1 分布式存储系统中的PIR

如果每个数据库只是分布式存储系统中的一个节点或者硬盘，那么每个数据库无需存储全部K条消息。但分布式存储系统的存储方案，要考虑下面两点需求：① 数据冗余需求,即在某些硬盘坏掉的情况下，剩余硬盘仍可以恢复全部数据；② 通信少的需求,即当产生新的硬盘来替代坏掉的硬盘保持冗余时，新硬盘与旧的可用硬盘之间的通信量要尽可能地少[13]。

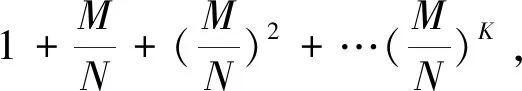
虽然MDS码在数据冗余方面表现优秀，它在满足通信量少方面却表现不佳[13]。因此，在MDS编码PIR问题研究成功后，人们开始探索非MDS码编码的数据库中，PIR的最小下载量是多少。 文献[15-19]研究了这类问题，并给出了若干非MDS码能达到MDS码PIR性能的条件。广泛的线性码下PIR的最小下载量仍是一个开放的问题。

3.2 数据库存储空间和PIR最小下载量的折中

通过对分布式存储系统中PIR的研究，人们发现，数据库存储的数据越多，PIR的最小下载量越小。因此，数据库存储空间大小和PIR最小下载量存在着一个折中。假设数据库的存储方式可以任意设计，那么最优折中能达到多少呢？

如果不做数据库存储不编码消息这一假设，那探求最优折中变得更加困难。文献[25]指出把不同消息编码在一起可以超越MDS码的存储空间和下载量折中，文献[26]提出了把MDS编码方案和不编码存储方案结合可以得到比MDS编码和不编码存储更优的折中，而文献[27]则探索了数据库存储非线性编码较线性编码的优越性，即非线性编码能够提供更优的折中。在数据库存储可以任意设计情况下的最优折中，至今仍是一个开放问题。

3.3 数据库存储部分完整的消息

前面两类问题中，假设数据库存储每个消息的编码或非编码的一部分。如果数据库存储空间大小受限，它也可以选择存储K条消息中的若干条完整的消息。文献[28]研究了每条消息都存在两个数据库上的情况，而文献[29]则研究了每个数据库能存两条消息的情况。这一类问题，除特殊情况外，最小下载量仍是开放问题。

把第一类变种问题和第二类变种问题结合到一起，也有不少论文的研究，例如分布式存储PIR加数据库共谋[30-36]、分布式存储加鲁棒PIR[37]、分布式存储加对称PIR加数据库共谋[38]、分布式存储加拜占庭加鲁棒PIR加数据库共谋[39]等。由于分布式存储系统下的PIR问题的复杂性，这些结合问题也基本都是开放问题。

4 第三类变种问题：用户有边信息的PIR

如果用户在不知道自己的检索需求之前，能够得到一些关于消息的边信息，此时这些边信息对PIR能有多少帮助？这是这一类变种问题研究并希望回答的。第三类变种问题中又分为两小类：

4.1 带存储功能的用户

如果用户有一定的存储空间，可以在知道自己检索需求之前先存一些关于消息的比特，那么这些预存比特对PIR有着什么样的帮助？这个问题的解答与预存比特下标是否为数据库所知有很大的关系。文献[40]指出，如果预存比特的下标是数据库知道的，那么最优方案为，平均预存每个消息的一部分，消息的剩余部分用文献[2]中最优检索请求来进行检索。也就是说，如果数据库知道预存内容的下标，那预存对用户来说帮助很小：除了预存的部分无需下载外，没有额外的帮助。针对文献[40]这个比较悲观的结论，文献[41-42]研究了另一个极端，即数据库对预存内容的下标一无所知的情况。由于问题的复杂性，它们额外做了一个假设，就是预存的只能是一些非编码比特。文献[42]提出的存储方案是均匀存储每个消息的部分比特，检索请求则再次用到了文献[2]中提出的消息对称性及数据库对称性。不同的是，由于数据库不知道预存内容，预存的非感兴趣数据可以优先拿出来单独或者以k项和的形式在每个数据库重复利用。文献[42]证明，在用户存储空间较小或较大，或者只有3个消息的时候，其提出的存储与检索请求方案是最优的。其他情况下，文献[42]刻画了最小下载量上下界的差距。文献[43]在数据库完全知道[40]和完全不知道[41-42]的两种假设下做了一个折中，它认为从哪个数据库得到的预存比特，那个数据库就知道这些预存比特下标，而其他数据库对这部分预存内容的下标一无所知。在这种情况下，文献[43]得出的结论与文献[42]类似，即在用户存储空间较小或较大，或者只有3个消息的时候，最优存储与检索请求方案已找到。其他情况下，文献[44]给出了最小下载量上下界的差距。

4.2 用户知道某些消息的完整内容

用户通过其他用户或者其他传输，得知了某些消息的完整内容或者某些消息线性组合的内容，这些内容被称为边信息。这些边信息虽然不是用户感兴趣的消息，它们能否帮助用户进行PIR呢？一系列研究指出，边信息分为两种情况，一种是边信息是用户不感兴趣的某些消息，另一种是边信息是某些消息的线性组合。此类问题还需考虑的一个关键在于是否需要保证边信息的下标不被数据库知道。如果边信息希望被重复利用，那么保护边信息的隐私对于用户来说也很重要。如果用户只用边信息一次，那么边信息的下标在检索请求中被泄漏也没有关系。因此，此类问题被分为4种情况：① 保护消息边信息的下标[44-45]；② 不保护消息和边信息的下标[46]；③ 保护线性组合边信息的下标[47-48]；④ 不保护线性组合边信息的下标[48-49]。目前已知最优解的情况是①及①②③的单数据库场景。其他的情况还属于开放性问题。

5 其他变种问题和性能指标

还有一些有意思的PIR变种问题，每个问题研究的文章较少。比如多消息PIR，即用户请求的消息多于一个，一个消息一个消息的私密请求是可以的，但是能否做到更好？文献[50]研究了此种情形，并在请求消息数多于全体消息数一半时，寻求到了最优检索请求方案。再比如数据库流量非对称的PIR[51]，如果每个数据库下载量占总下载量的比例给定且不相等，那么文献[2]中检索请求的数据库对称性就必须被破坏，此时，最优检索请求是什么？文献[51]在消息数等于2或3时，找到了该问题的完整解，然而其他情况还属于开放问题。再比如数据库到用户的通信信道并不是没有噪声的完美信道，文献[52-53]在这方面做了一些尝试，但是目前对此种问题的理解还远远不够。

传统PIR考虑的性能指标是满足解码条件和私密条件下的最小下载量，但是其实PIR问题还有许多其他人们关心的性能指标，例如：① 隐私条件放松后，隐私泄漏量和最小下载量的折中[54-55]；② 最小的消息长度[3，56-61]，该值小说明消息需要分块的数量少、编码操作的复杂度低；③ 上传代价最小[3]；④ 数据库计算复杂度低[62-63]；⑤ 数据库读取复杂度低[64]。

6 结束语

信息论中私密信息检索问题与一般信息论问题不同，一般信息论问题关心的是消息内容的传输、保密等，而私密信息检索问题关心消息下标的保密。很多私密信息检索问题都可以使用线性码、信息论工具和方法等推导出工整的最优解，这大大增强了人们对隐私保护的理解，提供了许多有效的隐私保护方法。信息检索只是隐私保护的一个方面，把私密信息检索问题的隐私保护框架放入更多的通信实际问题中，例如文献[65-66]，是未来一个很有前景和应用价值的研究方向。