FRACOD模拟软件在岩石工程中的应用及案例分析
沈宝堂,2,张步初,张士川,陈 兵
(1.山东科技大学 矿山灾害预防控制省部共建国家重点实验室培育基地,山东 青岛 266590;2.澳大利亚联邦科学院能源部 昆士兰先进技术中心,澳大利亚 昆士兰州 布里斯班 4069)
岩石断裂力学作为岩石力学及断裂力学的分支,近几年得到迅速发展,在基础研究及岩石工程设计等领域中得到了较为广泛的关注。随着岩石断裂力学涉及到更广、更具挑战性的领域(如深部开采、核废料地质储存、地热开发等),其扮演的角色显得更为重要。因此,岩石断裂力学的研究将是未来几年甚至几十年的热门课题。
目前阶段,室内岩石试验、数值模拟是岩石断裂力学的主要研究方法。室内岩石力学实验由于其可以直观展示裂纹的扩展及传播,因此得到广泛的应用。然而,受到岩石试样离散性的影响,室内试验结果往往存在较大偏差,数值模拟可以很好地解决该问题,同时,数值模拟可以有效展现裂纹扩展不同时刻内位移场、应力场和渗流场的分布特征,故数值模拟软件作为研究岩石断裂力学的手段逐步受到青睐。近年来,众多模拟固体断裂的数值软件应运而生。但大多数模拟软件是为土木工程和材料科学需求而开发的,并主要用于解决钢、陶瓷、玻璃等材料的裂纹扩展问题。显然这些材料在断裂性能上与岩石有着本质的差别。而且现有的模拟岩石裂纹扩展软件无法模拟剪切裂纹和混合裂纹的扩展。因此,急需开发一种可以模拟岩石混合裂纹(Ⅰ型、Ⅱ型、Ⅰ+Ⅱ型)扩展的软件。
为满足模拟岩石混合裂纹的需要,Shen等[1-3]基于岩石断裂力学原理及F-准则,开发了一种能够模拟岩石混合裂纹扩展的软件,为相关领域的研究提供了一种新的手段。Barton等[4]基于FRACOD2D软件,分别研究了完整岩石、含一组节理岩石、含两组节理岩石的裂纹扩展模式;Jung等[5]借助FRACOD进行了花岗岩巴西劈裂试验,测定了亚临界状态裂纹增长指数,并借助声发射事件数定量描述了裂纹数量;Li等[6]以FRACOD为手段,研究了脆性岩石的裂纹扩展过程及破坏特征;Shen等[7]利用FRACOD2D模拟了各向异性岩石的裂纹扩展规律,对岩石工程具有重要的指导意义;Zhang等[8]通过FRACOD模拟结果与物理试验结果之间的对比,成功验证了FRACOD模拟钻孔泄压具有可行性;Siren等[9]通过FRACOD对岩石破坏前的声发射特征进行预测,并将预测结果与实际观测的声发射特征进行了比较。
以上学者通过室内试验、理论分析等手段成功验证了FRACOD软件在相关领域的可行性。为进一步验证该模拟软件在岩石裂纹扩展领域的广泛适用性,本研究首先从理论基础方面对FRACOD模拟软件的工作原理进行了详细介绍,然后对三个应用案例进行模拟验证分析,相关结果对岩石工程设计领域发展具有重要的指导意义和参考价值。
1 FRACOD理论背景
FRACOD本质上属于边界元方法,遵循边界元原则。具体而言,其采用了间接边界元的位移非连续法。FRACOD以岩石断裂力学理论和F-准则为理论基础,对岩石混合裂纹扩展进行模拟。
1.1 基于位移不连续理论的岩石破裂模拟概况
假设无限弹性体X-Y平面中有一恒定的位移不连续直线单元,除该部分外,位移处处连续。直线段在x轴上|X|≤a,y=0,假设其为线性裂纹,定义其中一个面为y=0的正面,表示为y=0+,另一个为负面,表示为y=0-,在从裂纹一个面移动到另一个面的过程中,位移会产生恒定变化值Di=(Dx,Dy)。定义Di作为两边位移差:
(1)
ux和uy沿x轴正方向,则Dx和Dy为正,如图1所示,应力和位移可表示为
(2)
其中,f,x,f,y,f,xy,f,xxy表示函数f(x,y)相关导数,则:
(3)
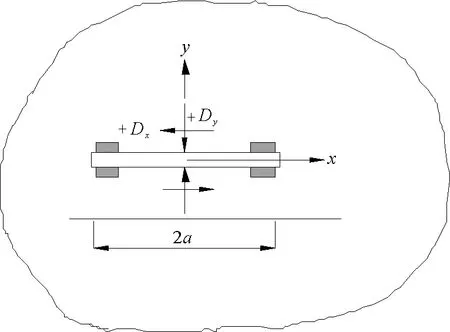
图1 非连续位移分量[10]
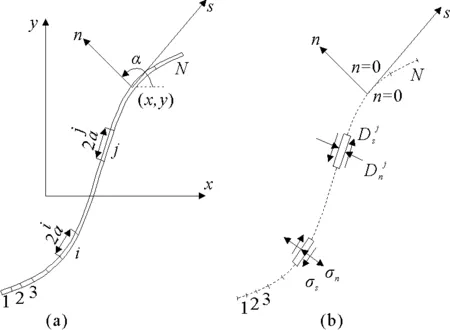
图2 裂纹单元体形式[10]
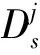
(4)

(5)
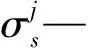
岩体的非连续可分为三个阶段,根据裂纹剪切应力与法向应力不同,不同阶段可表示为:
(6)
(7)
式中:Ks和Kn为节理剪切刚度与法向刚度,将式(7)代入式(6)得:
(8)
3)裂纹滑动破裂:
(9)
式中:θ—裂纹内摩擦角;c—粘聚力, 滑动后c=0。将式(9)代入式(6)得:
(10)
每个裂纹单元的状态均可通过Mohr-Coulomb破裂准则进行判定:
1)张开节理:σn>0;
2)弹性节理:σn<0,|σs| 3)剪切节理:σn<0,|σs|≥c+|σn|tanθ。 Shen等[10-11]提出了基于最大应变能释放率的F-准则来预测裂纹传播。F-准则将裂纹尖端应变能释放率分为两部分:Mode I和Mode II,二者之和决定裂纹起裂及传播方向。假设裂纹在任意方向传播一个单位长度,新裂纹为张开裂纹,没有任何剪切错动,则应变能损失为GI;同理,新裂纹若只有剪切错动,没有张开裂纹,则应变能损失为GII,那么F-准则可表示为: (11) F(θ)|θ=θ0=max, (12) F(θ)|θ=θ0=1.0。 (13) 式(11)中,GI(θ)和GII(θ)为最大应变能释放率,GIc和GIIc为材料强度参数。式(12)中,当θ=θ0时,F为最大值,则θ0为裂纹传播方向;式(13)中当F值为1.0时,裂纹开始起裂并扩展。 线弹性体中应变能 (14) 式中:σij—应力张量;εij—应变张量。应变能可通过边界处的应力应变进行计算: (15) 式中:σs—弹性体边界处的切向应力;σn—弹性体边界处的法向应力;us—弹性体边界处的切向位移;un—弹性体边界处的法向位移。将式(15)代入受远场法向应力与剪切应力的无限体裂纹系统中得: (16) 式中:a—裂纹长度;Ds—裂纹剪切非连续位移;Dn—裂纹法向非连续位移。利用位移非连续边界元进行计算,应变能亦可以表示为: (17) G的预测值为: (18) 式中:W(a)—原始裂纹应变能;W(a+Δa)—裂纹扩展后应变能,Δa为裂纹尖端沿θ方向次生裂纹扩展的距离,如图3所示。 图3 裂纹尖端扩展[10] 图4 完整岩石拉伸或剪切裂纹起裂[10] Shen等[10]结合位移非连续边界元与F-准则开发了岩石混合裂纹扩展软件FRACOD。初始岩体假设为无损伤、各向同性的均质介质,但局部可破裂产生新的裂纹。完整岩石的破裂可通过Mohr-Coulomb准则、Hoek-Brown准则等进行预测。如图4所示,当岩石某点拉伸应力大于其拉伸强度时,则拉伸裂纹开始起裂。 (19) 式中:σtensile—某点的拉伸应力;σt—完整岩石的拉伸强度;θit—拉伸裂纹起裂方向;θ(σtensile)—拉伸应力方向。裂纹起裂长度由完整岩石内网格尺寸所决定。 对于剪切裂纹,当某点剪切应力大于其剪切强度,则剪切裂纹开始形成。 (20) 式中:σshear—θis方向的剪切应力;σn—剪切破坏面上的正应力;θ—内摩擦角;c—内聚力;θis—最小剪切阻力方向,也是潜在剪切破坏面。裂纹扩展长度由完整岩石内网格尺寸所决定。 FRACOD研发的最终目的是为模拟实际工程中出现的断裂损伤、裂纹扩展等问题。近年来,FRACOD在钻孔破裂、矿柱剥落、水压致裂、巷道及竖井的稳定性等[9,12-17]方面得到了广泛应用。为验证FRACOD在岩石工程设计领域的可行性,对岩石力学双轴压缩试验、地热开发钻孔破裂、水压致裂等三个案例进行模拟验证分析。 地下工程施工过程中,如煤层开采、巷道开挖和隧道掘进等,施工周围岩体常处于双向受力状态,周围岩体的承载能力较三向受力状态明显下降,一旦失稳,将会带来灾难性的后果,严重威胁着施工人员的生命安全。因此,有必要对施工周围岩体的强度变化及裂纹扩展规律进行分析。根据前面对FRACOD理论基础分析可知,FRACOD可用于模拟双轴压缩试验。故采用FRACOD模拟双轴压缩过程中岩体的轴向应力变化及裂纹扩展规律。同时,为验证该模拟结果的准确性,将模拟结果与室内试验结果进行对比验证。 试验采用的试样长度为120 mm,宽度为60 mm。为模拟非润滑接触条件(强摩擦),试验过程中,限制了试样顶部和底部边界的水平移动。试样的顶部和底部边界分别施加了垂直压缩位移,侧边界施加10 MPa的约束应力。在每一步的计算中,增加竖直相对位移0.01 mm,直至试样破坏为止。根据前期试验经验[20],假定本次试验完整岩样的弹性模量为60 GPa,泊松比为0.25,内聚力为38 MPa,内摩擦角为30°,拉应力为13.4 MPa。I型和II型裂纹断裂韧度值分别为1.2 MPa·m1/2和3.0 MPa·m1/2。 本次模拟采用了Mohr-Coulomb强度准则及随机裂纹起裂函数,并且将初始起裂应力水平设定为岩石强度的50%。模拟试验加载过程中裂纹起裂和扩展的预测过程如图5所示。 图5 双轴应力压缩作用下岩样裂纹的起裂、扩展及最终破坏的预测过程[20] 图6为FRACOD模拟双轴加载试验过程中的应力-应变曲线。轴向应力为80 MPa时裂纹开始起裂,应力-应变曲线偏离初始的线性关系,变为非线性。当施加的应力达到125 MPa左右时,裂纹快速扩展并贯通,当岩样的轴向载荷达到130 MPa时,其形成一个较大的剪切破坏面。峰后阶段裂纹继续扩展,整体承载能力降低。最终,试样完全破坏,残余强度约为60 MPa。此次模拟试验结果与室内试验结果基本一致,说明FRACOD可以很好地模拟双轴压缩试验。 图6 双轴压缩模拟过程中的应力-应变曲线[15] FRACOD于2002年开始用于模拟澳大利亚干热岩地热能开采过程中的深部花岗岩钻孔破裂过程[18]。在该案例中由于钻孔深度较大(>4 000 m),现场地应力测量难以实施,尤其最大和最小主应力值均难以确定,这为后期工程方案设计和施工带来较大影响。为此,进行了钻孔破裂形态的现场观测,并利用FRACOD软件模拟了岩体主应力的分布情况。通过澳大利亚实测数据与模拟结果的对比验证了FRACOD模拟的准确性。 首先,通过声波扫描获得了深度3 000~4 500 m段注入井的破裂宽度,并借助卡尺等工具测量了注入井的破裂深度。注入井典型的破裂扫描图像如图7所示,其中破裂宽度角约为62°,实测破裂深度约为钻孔半径的23%。 图7 钻孔破裂测量值与FRACOD模拟值比较[20] 基于以上现场观测结果,采用FRACOD软件进行注入井典型的破裂过程的模拟。由于注入井深度4 500 m处的压力过大(大于35 MPa),温度过高(约240°),难以获得力学参数,故本次模拟过程选用了文献[14]获得的花岗岩力学参数,即:弹性模量65 GPa,泊松比0.25,内聚力31 MPa,摩擦角35°,单轴抗压强度120 MPa,I型裂纹断裂韧度值为1.35 MPa·m1/2,II型裂纹断裂韧度值为3.07 MPa·m1/2。 FRACOD模型中分析了大量的最大和最小水平主应力组合。对于最大水平主应力为60 MPa(减去空隙水压的有效应力)、最小主应力为30 MPa的组合,预测的破裂角为58°、深度约为钻孔半径的26%,如图7(b)所示。通过对多个应力组合的模拟,得出了两主应力组合与钻孔破坏的宽度及深度的关系,最后根据在不同深度测得的实际钻孔破坏尺寸反算出该处的水平应力大小。结果表明,该地区的原岩水平应力均大于竖直应力。 在后续的钻孔水压致裂工程中,根据微地震监测数据,裂隙的传播都在一个近水平的平面上,证实现场竖直应力为最小主应力。FRACOD所模拟的应力与深井花岗岩的实际观测值相吻合。该模拟结果验证了FRACOD在模拟钻孔破裂方面的可行性。 FRACOD亦可应用于水压致裂方面的研究。为验证FRACOD在模拟水压致裂方面的可行性,进行了水压致裂模拟试验研究,并将模拟结果与Tsukada课题组的注水压裂室内试验结果进行对比验证。 Tsukada等[21]配制了含两条交叉预制裂隙的方形砂浆试件,并对该试件进行了水压致裂试验。结果表明,次生裂纹大致沿预制裂纹方向扩展。当采用FRACOD模拟该室内试验过程时,预测到该试件主要呈剪切裂纹扩展模式,如图8所示。通过对比发现,FRACOD预测的裂纹扩展路径及临界载荷与室内试验结果基本一致,证明了FRACOD软件可准确模拟水压致裂。 图8 裂缝扩展观测与预测的比较[20] 1)基于岩石断裂力学理论及F-准则,开发了能够模拟岩石混合裂纹扩展的FRACOD软件,可以准确模拟岩石的Ⅰ型、Ⅱ型和Ⅰ+Ⅱ型裂纹扩展、应力场、位移场等物理参量的变化特征。该软件对岩石工程设计领域发展具有重要的指导意义和参考价值。 2)从理论方面对FRACOD进行了详细的介绍,软件以间接边界元的位移非连续法为基本理论,引入Mohr-Coulomb准则模拟裂隙的起裂,以及F-准则模拟混合型裂隙扩展及破坏特征。在此基础上,通过钻孔破裂、双轴压缩、水压致裂三个模拟试验进行了案例分析验证。通过模拟试验结果与室内试验或现场观测结果对比发现,FRACOD可以准确模拟岩石的混合裂纹扩展,在众多工程领域具有适用性。 笔者开发的FRACOD软件不仅可以模拟单一场的裂纹扩展,而且还相继研发了H-M(液-力)耦合模块、H-T(液-热)耦合模块、H-T-M(液-热-力)耦合模块用以模拟多场耦合作用下的裂纹扩展规律及岩体破坏特征。在后期工作中,将会一一进行详细介绍。1.2 基于应力释放率的F准则及FRACOD
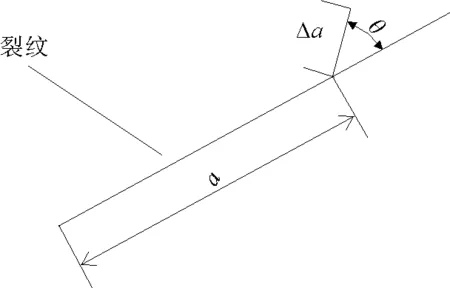

2 工程应用案例分析
2.1 模拟双轴压缩试验
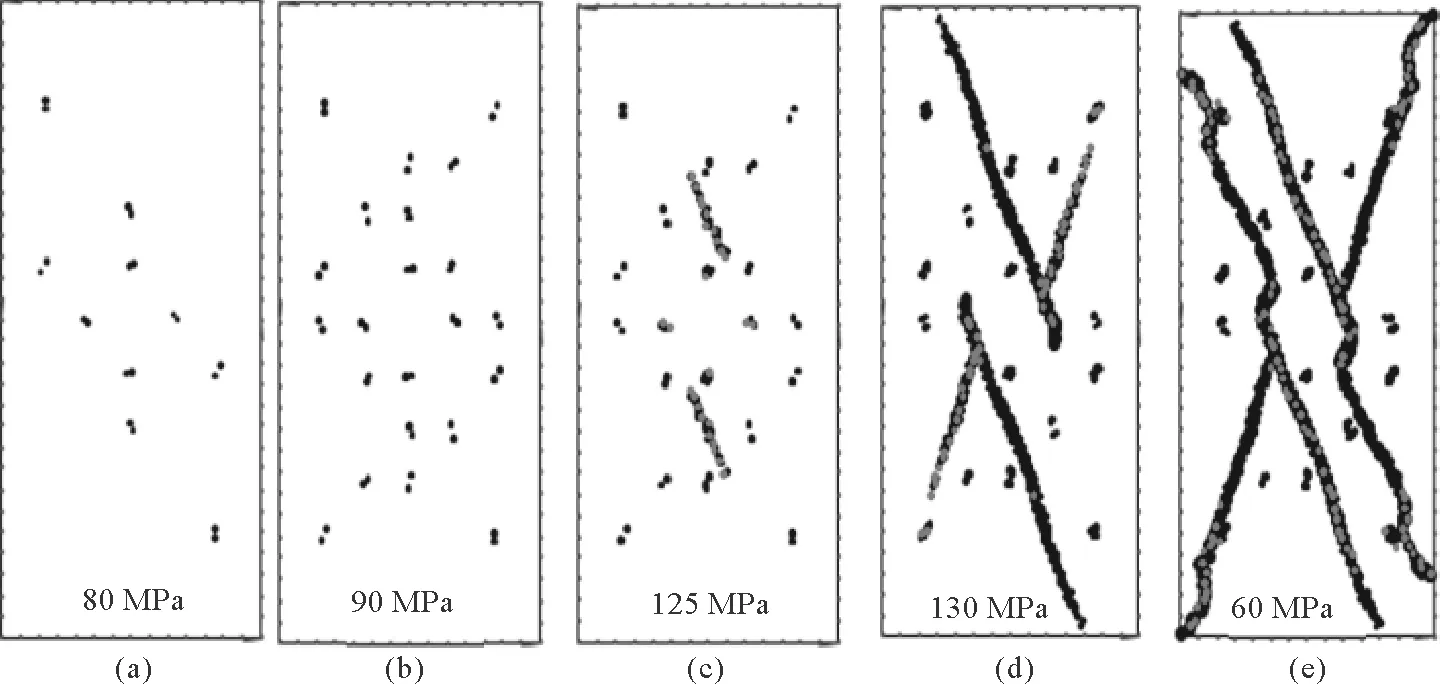
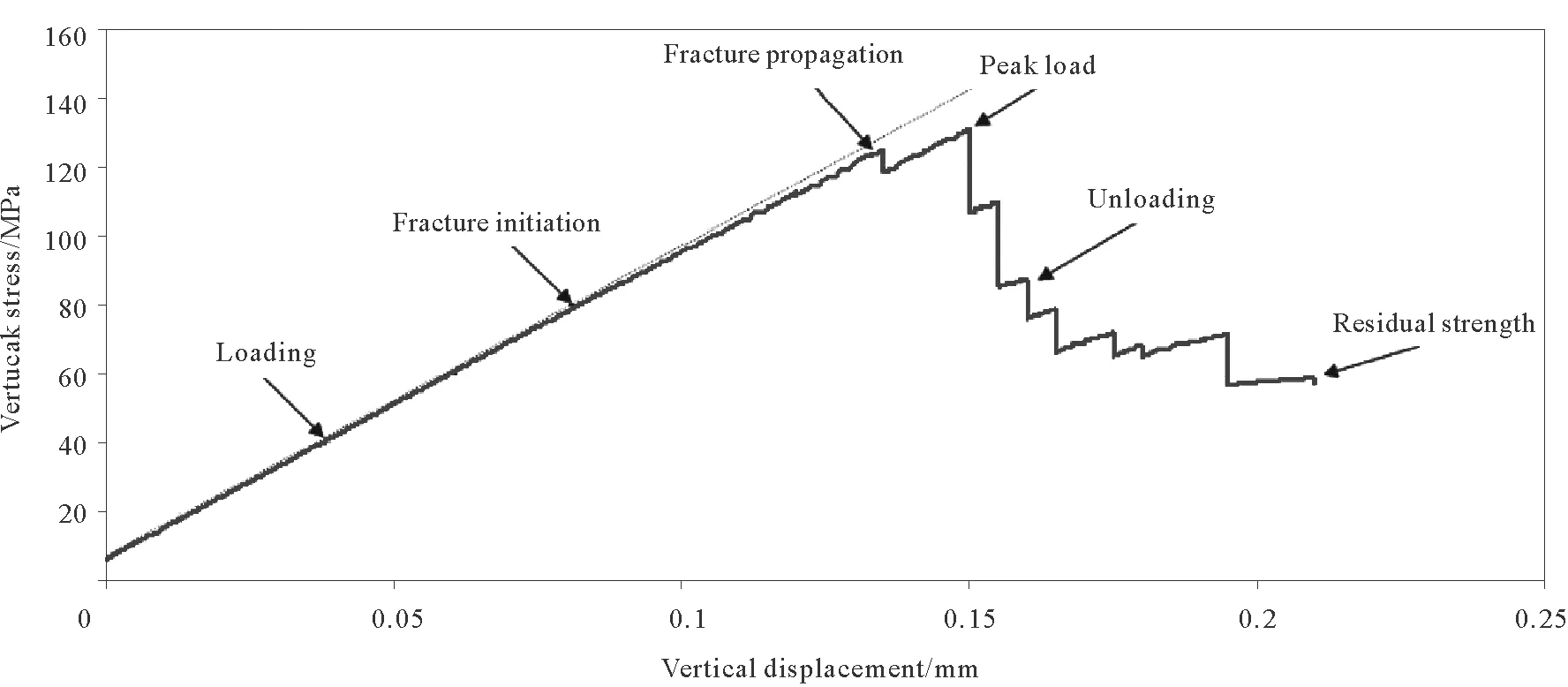
2.2 模拟钻孔破裂
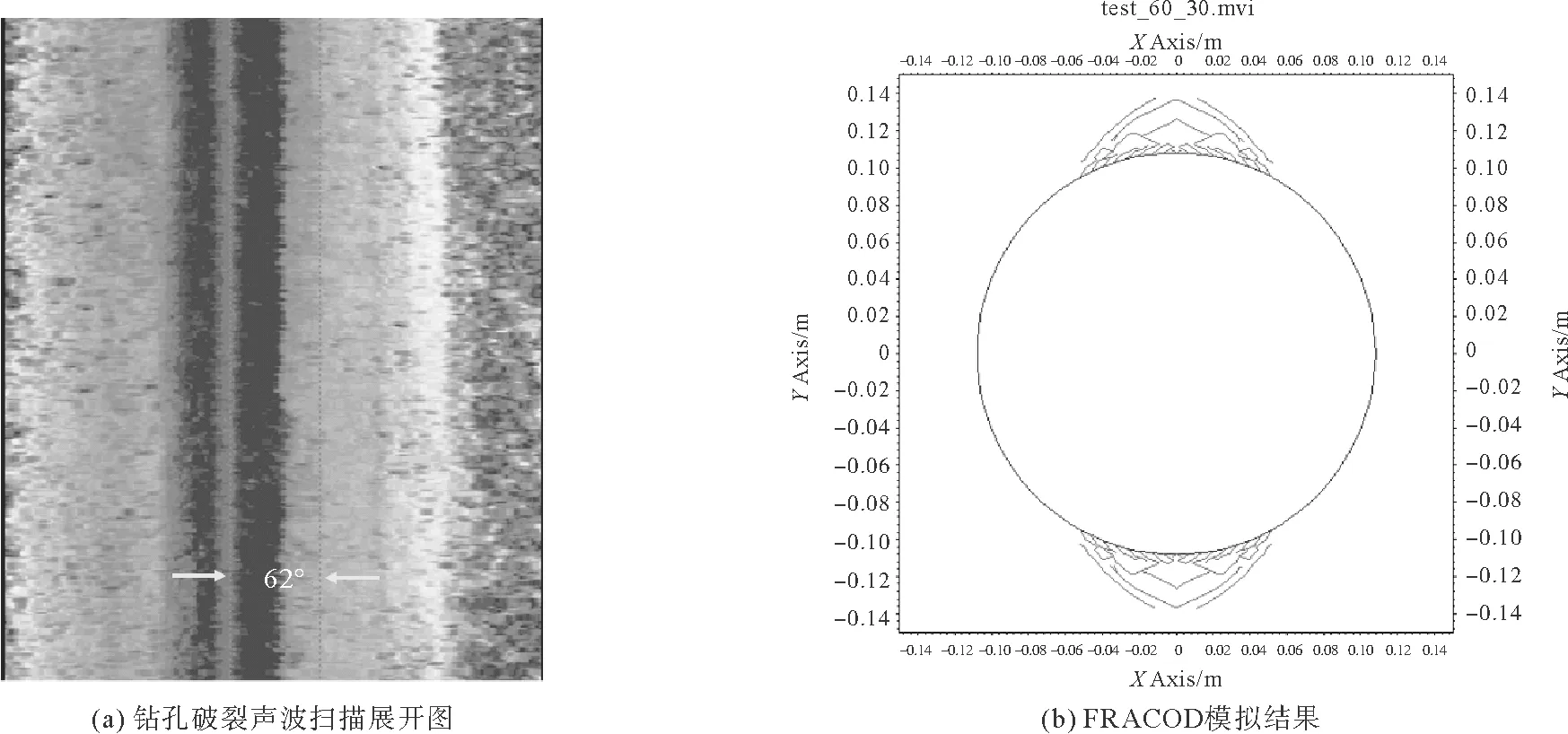
2.3 模拟水压致裂

3 结论

