天然气水合物分解-两相渗流数值模拟研究

13

(1.山东科技大学 矿山灾害预防控制省部共建国家重点实验室培育基地，山东 青岛 266590；2.山东科技大学 矿业与安全工程学院，山东 青岛 266590；3.昆士兰大学 机械与采矿工程学院，澳大利亚 昆士兰州 布里斯班4072)

天然气水合物被称作“可燃冰”，是一种高能量密度的新型能源，具有极高的资源价值[1]。我国水合物储量巨大，海域水合物储量约800亿t油当量[2]。天然气水合物开采的基本思路是人为打破其相平衡条件，目前降压法是应用最广泛的水合物试采方法。针对水合物降压开采过程中储层物理参数演化问题，国内外学者开展了一系列的研究。李淑霞等[3]根据神狐海域水合物资料，采用数值模拟研究了降压速度对水合物开采动态的影响。于明豪[4]采用有限差分法研究了含冰相水合物降压开采过程中的参数相互影响规律。刘乐乐等[5]通过松散沉积物中水合物降压分解阵面演化实验，研究了水合物阵面的传播规律。郝天翔[6]采用有限体积法软件Fluent研究水合物降压过程中的多相流动和化学反应，分析了压力等参数对分解速率的影响规律。刘丽强等[7]采用TOUGH+HYDRATE对南海水合物降压开采进行数值模拟，通过不同等级的参数敏感性分析了水合物储层的参数演化规律。程远方等[8]基于应力敏感性建立了水合物物性参数与水合物饱和度的关系模型，全面研究了水合物分解对储层物性参数的影响。刘建军等[9]建立了THMC模型，研究不同参数对产气效率的影响规律。

目前天然气水合物主要聚焦在室内试验和水合物分解动力学方面，针对不同因素对水合物开采过程中储层各参数的影响规律研究较少。本研究建立了耦合水合物化学分解和气水两相渗流的数值模型，考察降压幅度、初始绝对渗透率和含水饱和度对储层物理参数的影响规律。

1 天然气水合物分解理论模型

1.1 模型假设

天然气水合物开采过程存在物理和化学变化，是一个多相多组分的复杂过程，为评估水合物分解过程中其物理特性的变化规律，需建立一个耦合多个物理场的FEM模型，假设：

1)鉴于I型立方晶体结构水合物在自然界中分布最广泛[10]，假设水合物结构为I型；

2)水合物中气体为纯甲烷，无次生气体，液体为纯水，不考虑甲烷在水中溶解性；

3)甲烷和水的流动符合达西定律，为饱和两相渗流，不考虑沉积物与流体之间化学作用；

4)甲烷和水为饱和两相渗流，且不考虑沉积物与流体之间的化学作用；

5)不考虑开采过程中温度变化，忽略水合物在多孔介质中的二次生成现象。

1.2 天然气水合物分解动力学方程

天然气水合物生成-分解化学方程式为CH4·NhH2O↔CH4+NhH2O，天然气水合物的相态由气体压力和温度控制，其相平衡方程[11]为：

(1)

式中：Pe为相平衡压力，MPa；e1、e2为回归系数；T为温度，K。

天然气水合物相平衡曲线如图1所示，当压力和温度处于相平衡曲线及以上时，水合物以固态形式稳定存在于多孔介质中，其分解与生成速率达到一个动态平衡；当压力与温度在相平衡曲线以下时，水合物的动态平衡被打破，其分解速率大于生成速率，宏观上表现为水合物分解，由固相逐渐转变为气相和液相。

天然气水合物的分解可采用Kim-Bishoni 分解动力学方程[12]来描述，分解速率为：

mh=-kdMhAs(Pe-Pg)。

(2)

式中：As为水合物反应比表面积，1/m2；Mh为水合物摩尔质量，kg/mol；Pg为气体动态压力，MPa。

图1 天然气水合物相平衡曲线

kd为动力学反应速率，Pa·s，与温度成负相关。

(3)

反应比表面积与孔隙率、水合物饱和度和绝对渗透率有关，计算公式为：

(4)

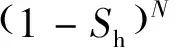
由上述公式可以得到水合物的分解速率

(5)

水合物分解质量守恒方程为：

(6)

根据水合物分解化学式可知，天然气水合物产气速率和产水速率分别为：

(7)

(8)

式中：MCH4、MH2O分别为甲烷和水的摩尔质量，kg/mol。

1.3 气水两相渗流方程

天然气水合物储层气、水两相流动的质量守恒方程[13]分别为：

(9)

(10)

式中：Pw为水的动态压力，MPa；Sg、Sw分别为甲烷和水的饱和度；krg、krw分别为甲烷和水的相对渗透率；ug、uw分别为甲烷和水的动力粘度，Pa·s；ρg、ρw分别为甲烷和水的密度，kg/m3。

甲烷密度采用理想气体状态方程：

(11)

天然气水合物相、气相和水相三相共同占据孔隙空间，各相饱和度关系为：

Sh+Sg+Sw=1。

(12)

毛细管力对气水两相渗流具有明显的影响，大小为润湿相与非润湿相的差值，通过该定义可将式(9)和式(10)统一为Pg的函数，公式为：

Pc=Pg-Pw。

(13)

同时毛细管力与水有效饱和度有关[14]，计算公式为：

(14)

相对渗透率通常为润湿相有效饱和度的函数，目前相对渗透率模型都是基于不同流体在不同多孔介质中的驱替实验数据[15-18]提出的，相对渗透率模型采用Leverett[18]提出的公式：

(15)

(16)

式中：λ是与孔径分布有关的系数；m为相对渗透率系数；se为有效饱和度，定义为：

(17)

式中：Swr为水的残余饱和度；Sgr为甲烷的残余饱和度。

根据式(9)～(17)，气体和水的质量守恒方程可以写为：

(18)

(19)

其中：

(20)

2 物理模型的建立与求解

水合物开采几何模型如图2所示，以边长100 m的井田作为研究对象，采用天然气水合物试采工程中的单井布置，由于模型结构的几何对称性，为提高计算效率，取其四分之一建立边长50 m的二维模型，开采井位于模型左下角，井筒半径为0.15 m。储层初始压力为3.75 MPa，温度为275.45 K，孔隙度为0.35，无水合物绝对渗透率为100 mD，水合物饱和度为0.45，降压幅度为2 MPa。周围边界设置为无流动边界条件，开采井井筒为降压边界，数值模拟参数见表1。

图2 水合物开采几何模型

描述天然气水合物分解-气水两相流动的方程是非齐次的复杂偏微分方程组，具有强烈的非线性，常规手段无法得到其解析解。COMSOL Multiphysics提供了一个基于偏微分方程的建模环境，可通过有限单元法计算偏微分方程数值解。通过COMSOL求解耦合偏微分方程组，其中式(1)～(8)求解采用了域常微分接口，式(9)～(20)求解采用了一般形式偏微分接口。

模型求解后储层压力和水合物饱和度变化如图3所示。井筒开始排水降压后，储层的甲烷和水在压力差的驱动下逐渐向井筒流动，井筒附近形成压降漏斗，储层压力随时间逐渐减小，且压降辐射范围随着时间逐渐增大，降压30 d后，压降影响范围扩大到23 m。水合物储层初始温度为275.45 K，水合物相平衡压力为3.46 MPa，与初始储层压力仅相差0.26 MPa，井筒附近储层压力迅速下降为3.46 MPa以下，水合物开始分解，饱和度逐渐下降。水合物分解区域和压降范围呈现明显的一致性，随时间逐渐增大，开采至30 d时，水合物分解边缘距井筒约22.5 m。

表1 数值模拟输入参数

图3 储层压力和水合物饱和度变化

3 天然气水合物降压开采参数敏感性分析

目前降压开采为天然气水合物试采工程中最常用的方法，但试采工程中不同因素对产气速率、水合物饱和度和渗透率等参数的影响规律仍不够明确。因此，本节讨论影响天然气水合物产气速率、水合物饱和度和渗透率等关键参数的因素，分析其敏感性，这些因素包括降压幅度、储层初始绝对渗透率和储层初始含水饱和度，见表2。

表2 不同敏感因素数值模拟参数表

3.1 不同降压幅度

监测点坐标为(5 m，5 m)，通过该监测点分析降压幅度分别为0.5、1.0、1.5和2.0 MPa时水合物产气速率、水合物饱和度和渗透率的变化，如图4所示。井筒开始降压后短时间内产气速率达到峰值，然后逐渐下降为一定值，如图4(a)所示。初始快速产气是由储层游离气体流动和水合物分解共同作用，由于井筒的突然降压，井周气体流速较大，所以降压初期产气速率较大，气体流速随着时间逐渐稳定，产气速率也随之平稳。模拟结果显示降压幅度为0.5 MPa时产气速率峰值为344 m3/d，降压幅度为1.0、1.5和2.0 MPa时产气速率分别为1 050、1 630和2 170 m3/d，较0.5 MPa分别增长了2.05、3.74和5.31倍。产气速率到达峰值后开始逐渐下降，最终以稳定速率产气，分别为260、713、1 083和1 387 m3/d。

不同降压幅度下水合物饱和度和储层渗透率变化如图4(b)所示。降压开始后，当压降传递到该监测点处，该点水合物开始分解，其饱和度逐渐降低，直至完全分解，饱和度大小为0。降压大小越大，水合物越早开始分解，分解速率也随之增大。降压幅度0.5 MPa时水合物完全分解耗时22 d，降压幅度1.0、1.5和2.0 MPa时水合物完全分解分别耗时7.46、3.81和3.14 d，分别为0.5 MPa的0.34、0.17和0.14倍。由Masuda渗透率下降模型可知，含水合物沉积物绝对渗透率和水合物饱和度成负相关，如图5所示，渗透率随着水合物饱和度增大而减小。所以图4(b)显示降压幅度越大，水合物越早开始分解，渗透率也越早开始增大。

图4 不同降压幅度下水合物各参数变化

图5 渗透率随水合物饱和度变化

3.2 不同初始绝对渗透率

不同初始绝对渗透率下产气速率如图6(a)所示。渗透率是评价流体通过多孔介质能力的基本指标，渗透率越大，气体在储层中更易流动，所以井筒开始降压后短时间内产气速率达到峰值，且该峰值随着储层绝对初始渗透率的增大而增大，渗透率为50、100和200 mD时的产气速率峰值分别为渗透率25 mD时的1.61、2.72和4.69倍。

不同绝对初始渗透率下水合物饱和度和储层渗透率变化如图6(b)所示。降压开始后，当压力传递到该监测点处，该点水合物开始分解，饱和度逐渐降低，直至完全分解。降压速度与渗透率的大小成正比，渗透率更大的储层会更快达到井筒压力，所以渗透率越大，水合物越早开始分解。同上，由Masuda渗透率下降模型可知，含水合物沉积物绝对渗透率和水合物饱和度成负相关，所以渗透率越大，水合物越早开始分解，渗透率越早开始增大。

图6 不同初始绝对渗透率下水合物各参数变化

图7 相对渗透率变化曲线

3.3 不同初始含水饱和度

由图7可知，水的相对渗透率随含水饱和度的增大而增大，气体相对渗透率则相反，与含水饱和度成负相关。由第3.2节分析可知，产气速率随着气体流动能力的增大而增大，因此初始含水饱和度越大，气体相对渗透率越小，产气速率越小。不同初始含水饱和度下产气速率如图8(a)所示。井筒开始降压后短时间内产气速率达到峰值，该峰值随储层初始含水饱和度的增大而减小。初始含水饱和度为0.1、0.2和0.3时产气速率分别为含水饱和度0.4时的2.42、1.75和1.32倍。

不同初始含水饱和度下水合物饱和度和储层渗透率变化如图8(b)所示。气体相对渗透率随含水饱和度的增大而减小，且降压速度与渗透率的大小成正比，所以降压速度随含水饱和度的增大而减小，即储层初始含水饱和度越小，水合物越早开始分解。类似地，渗透率比随着水合物饱和度增大而减小，所以储层初始含水饱和度越小，水合物越早开始分解，渗透率越早开始增大。

4 结论

1)建立了涉及天然气水合物化学分解和气、水两相渗流问题的耦合数值模型，并采用有限单元法进行了求解。井筒开始降压后，井周迅速形成压降漏斗，压降辐射范围随时间逐渐增大，且水合物分解范围和压降范围呈现明显一致性。

2)井筒降压后短时间内产气速率达到峰值，降压幅度为1、1.5和2 MPa时产气速率峰值较0.5 MPa时分别增长了2.05、3.74和5.31倍；产气速率到达峰值后开始逐渐下降，最终以稳定速率产气，水合物分解速率和渗透率增大速率随降压幅度的增大而增大。

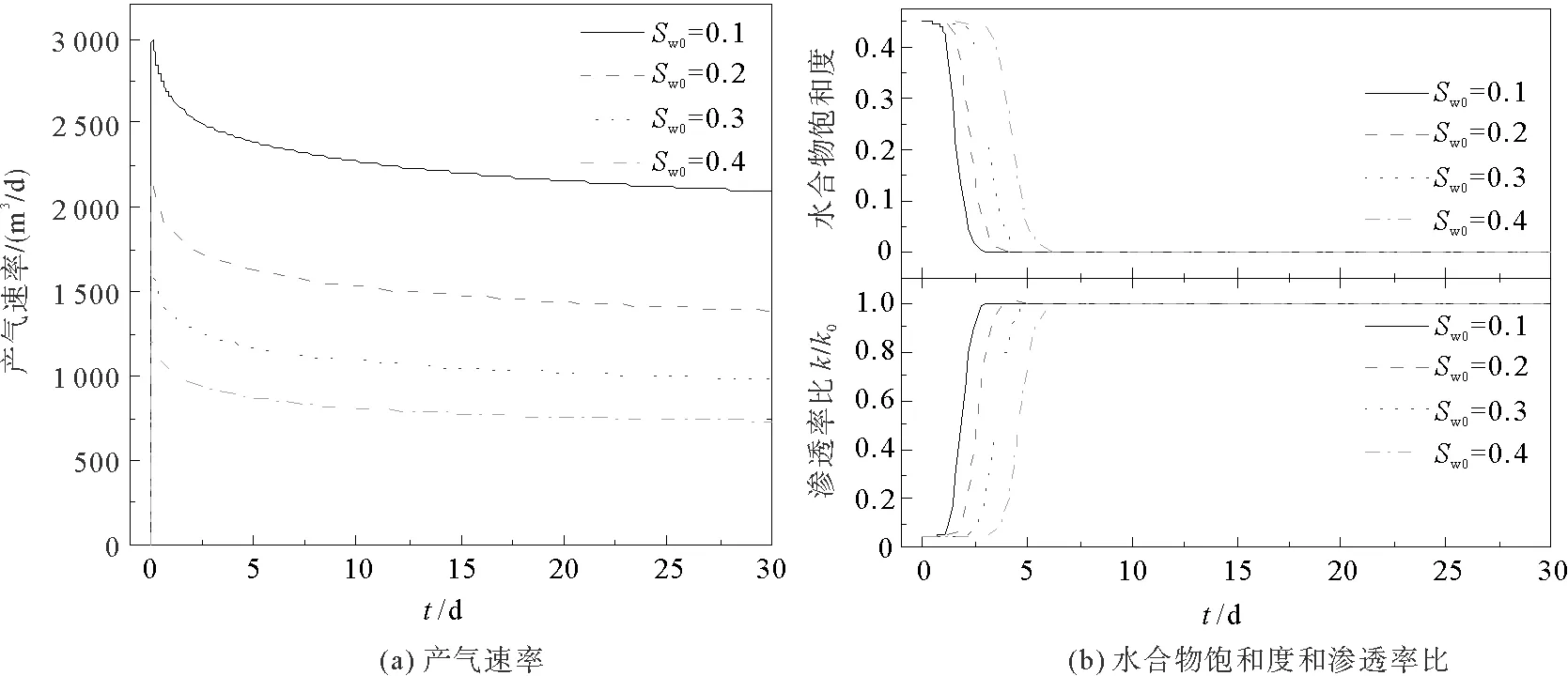
图8 不同初始含水饱和度下水合物各参数变化

3)产气峰值随着储层初始绝对渗透率的增大而增大，绝对渗透率为50、100和200 mD时产气速率峰值分别为渗透率25 mD时的1.61、2.72和4.69倍。绝对渗透率越大，流体的流动性越强，水合物越快开始分解，渗透率越快开始增大。

4)产气速率峰值随储层初始含水饱和度的增大而减小，初始含水饱和度为0.1、0.2和0.3时产气速率分别为含水饱和度0.4时的2.42、1.75和1.32倍。气体相对渗透率随含水饱和度的增大而减小，储层初始含水饱和度越小，水合物越快开始分解，渗透率越快开始增大。