基于粒子图像测速的锚板抗拔破坏机理试验研究

倪钰菲，乔仲发，朱泳，朱鸿鹄,3

(1. 南京大学 地球科学与工程学院，南京 210023；2. 浙江省交通规划设计研究院，杭州 310006；3. 南京大学(苏州)高新技术研究院，江苏 苏州 215123)

近年来，能源需求的增加使海洋开发建设朝着深海推进，悬浮结构、水下平台和海底油气管道等建设中均需要不同形式的锚固结构。同时，陆上的通信塔、悬索桥、人工边坡和基坑等也常需设置抗拔或锚定装置[1]。锚板因具有良好的抗拔承载特性，以及定位准确、施工时间短、对环境破坏小、经济性好等优点，成为一种广泛使用的结构基础形式[2]。

掌握锚板在土中拉拔时的变形破坏机制，对于预测锚板抗拔力有着重要的意义。在过去的几十年里，学者们在这一领域做了大量的研究，系统分析了影响其承载特性的众多因素，如锚板的形状、尺寸、埋置深度、地基土密实度、锚板拉拔速率等。刘明亮等[3]、Pérez等[4]、贾富利[5]、于龙等[6]、张昕等[7]均做过有关锚板抗拔承载特性的研究。

近年来，粒子图像测速(PIV)技术在土工模型试验中得到了成功的应用，该技术可实现全流场瞬态测量和无干扰测量，与常规的电测技术相比有很明显的优势，可获得以前无法观察到的土体精确变形及其分布情况[8]。笔者基于PIV技术和锚板拉拔试验，对锚板周围土体变形破坏的全过程进行实时测量，以深化对锚板抗拔破坏特征及破坏面的认识。

1 锚板抗拔破坏模式

对于锚板在土中的抗拔承载性能，现有的分析方法有极限平衡法、有限单元法和圆孔扩张理论等[9]。采用极限平衡法分析时，破坏模式的建立取决于对破坏面形状、应力沿破坏面分布的假定。众多学者对此开展了系统的研究。Meyerhof等[10]考虑了锚板的形状、埋深和砂土的内摩擦角，假定破坏面与竖直方向的夹角为φ/4～φ/2，φ为土内摩擦角。Chattopadhyay等[11]假定破坏面与锚板边缘相切并沿曲线向表面发展，破坏面与地面的夹角为45°-φ/2。Saeedy[12]假定破坏面与锚板边缘相切，形状为向土体表面扩展的对数螺旋线。锚板埋深不同时，破坏面不同，浅埋时破坏面由锚板边缘延伸至地面，深埋时破坏面延伸至地下一定深度，不到达地面。

在各种破坏面中，土体中锚板破坏的滑裂面形式基本分为3类：摩擦圆(柱状破坏面)、倒椎体和曲面[5]，如图1所示。当锚板浅埋时，破坏面一般为延伸至地表的土体楔形，破坏面多假设为直线、斜线或对数螺旋线。对于柱状破坏面，锚板的抗拔力由锚板正上方圆柱形破坏面内的土体重量加上竖直破坏面上的摩擦阻力组成；而倒椎体破坏面与竖直方向的夹角为φ，该破坏模式中锚板的抗拔力为破坏面内倒椎体的土体的重量；曲面破坏面是由锚板边缘延伸并与地面相交，夹角为45°-φ/2。对于深埋锚板，Meyerhof等[10]指出，破坏面中包含未达地面的深楔形土体。

综上所述，对于锚板上拔时周围土体变形破坏的模式尚未有共识，不同学者提出的破坏模型差别较大。因此，有必要采用先进的测量技术，对锚板的抗拔破坏机理进行更加精细化的研究。

2 PIV数字图像分析技术

粒子图像测速(particle image velocimetry，简称PIV)是利用图形图像处理技术发展起来的一种新型流动测量技术，其突出优点在于可实现全流场瞬态测量和无干扰测量，且可由全场的速度信息来求得流场的其他物理量，如压力场等[13]。PIV实现过程一般分为3步：通过硬件设备采集流场图像，应用图像处理算法提取速度信息，显示流场的速度矢量分布[14]。

近年来,PIV技术逐渐被应用于岩土工程试验研究[14-17]，基于灰度分布图像相关法、粒子分布图像相关法等关联算法，分析土体变形前后的两幅连续图像，可获得土体变形后的位移场。通过PIV计算得到的速度、剪应变率等数据，可分析砂粒的运动方式和应变积累，准确揭示土体的变形过程和机制[14-15]。在试验中用数码相机连续拍摄锚板周边土体，利用Geo-PIV软件分析照片即可掌握土体的变形规律。

3 锚板拉拔试验

3.1 试验设备及加载方式

通过拉拔试验探究锚板周边土体的破坏模式。试验设备由模型箱、半圆形锚板、金属连接杆、夹具、拉力计和位移计组成。如图2所示，模型箱底部为10 mm厚的铝板，四周为10 mm厚的透明有机玻璃板，内壁尺寸为500 mm×300 mm×500 mm。金属连接杆直径为5 mm，该杆穿过锚板质心连接到拉力计。试验所用拉力计量程为0～100 N，精度为±0.1%F.S.。位移计量程为600 mm，精度为0.5 mm。

有学者做了关于锚板模型试验的尺寸效应研究，研究发现：埋深比相同时，锚板承载力系数随锚板直径的增加而减小；埋深比增加时，不同直径锚板的上拔承载系数差别增大，尺寸效应更明显[5,9]。现有关于锚板拉拔的试验研究大多采用直径小于100 mm的锚板，不超过模型箱宽度的1/5，只有少数离心机试验和现场测试采用大尺寸锚板[5,10]。因此，本试验中锚板选用直径70 mm、厚度5 mm的半圆形金属锚板，其中，锚板与有机玻璃侧板相贴。在锚板上拔时，据Liu等[3,16]的研究，半圆形锚板与有机玻璃的界面摩擦会提供更高的抗拔力，但半圆形锚板与圆形锚板的破坏位移很接近，因此，锚板与侧板间的界面摩擦对土体在拉拔力峰值时刻及最终破坏面位移的影响可忽略不计，这意味着可采用半圆形锚板模拟圆形锚板，以确定土体的位移场[17]。

试验装置由图像获取系统、动力系统和数据采集系统3部分组成，如图2(b)所示。图像获取系统由佳能数码相机、三脚架、计算机和遮光帷幕4部分组成。数码相机由计算机控制，实现自动连续拍照。动力系统由万能材料试验机和计算机组成，由计算机程序控制试验机运行，万能材料试验机提供锚板竖向拉拔力。数据采集系统由加载设备、拉力计、位移计、数据线和计算机4部分组成，加载设备为万能试验机，通过锚板提供匀速的垂向拉力；拉力计和位移计实时同步获取并记录锚板的拉拔力和位移，由计算机实时监控并记录数据。

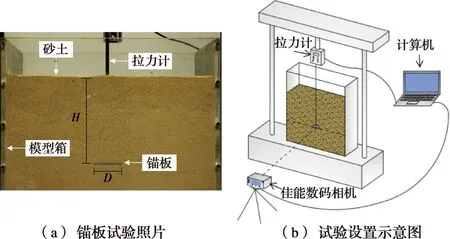
图2 锚板拉拔试验设备

3.2 土样参数及制备

试验所用砂土取自南京仙林某建筑工地，为级配不良砂，具体物理性质见表1。试验共展开4组模型试验，设计了2组不同密度的砂土地基，平均密度分别为1.40 g/cm3(松砂)和1.60 g/cm3(密砂)，对应的相对密实度分别为14.8%和76.2%。锚板埋置深度分为浅埋(H/D=1)和相对深埋(H/D=3)两种。在试样制备时，先按设计的地基土密实度和埋深称取所需的砂土质量，在模型箱底部铺设20 mm厚等密实度的砂土作为垫层。将连接好的半圆形锚板直边与有机玻璃板紧贴，如图2(a)所示，再分层填筑砂土地基并压实至预定高度。

表1 砂土试样的物理力学性质指标Table 1 Physical and mechanical properties of the test sands

3.3 试验步骤

1)首先将相机置于有机玻璃模型箱正面一侧约500 mm处，使其光轴垂直于模型箱，再调整焦距和ISO以获取最佳图像。测试过程中光源仅照亮有机玻璃面一侧砂土，并在相机和模型箱间设置黑色遮光帷幕，避免试验人员移动造成的阴影影响图片质量。

2)打开拉力计，激活计算机上的数据采集系统，设置自动采集频率为2 Hz；激活摄像机驱动程序，相机设置为自动拍摄模式，帧速率为每10 s摄取一帧。

3)通过计算机控制万能试验机给锚板提供竖向拉拔力，控制拉拔速率为5 mm/ min，并读取锚杆的载荷数据。当土体出现明显的滑裂破坏或当锚板拉拔力变化不大时，测试终止。

4 试验结果分析

4.1 锚板拉拔力与位移关系

由数据采集系统采集到锚板的拉拔力与位移数据，在多组试验数据中选取结果较好的数据，以深埋锚板(H/D=3)为例，二者关系曲线如图3所示。其中，密砂中锚板位移为38.5 mm时达到峰值拉拔力88.3 N；松砂中锚板位移58.3 mm时达到峰值拉拔力29.2 N。由拉拔力与位移关系可以看出，锚板拉拔过程主要分为两个阶段：峰值前的缓慢增长阶段、峰值后的波状缓慢减小阶段。曲线中峰值前锚板拉拔力随位移的增加先是快速增加，二者基本呈线性关系，出现拐点后进入缓慢增长阶段，以逐渐缓慢的速率达到峰值，峰值后拉拔力随位移增加缓慢下降，呈现波动减小状态。曲线特征是峰值前拉拔力随位移逐渐增加，峰值后逐渐减小。峰值后曲线波动较大是因为锚板上方土体变形，导致砂粒滑落至锚板下方空隙中引起。

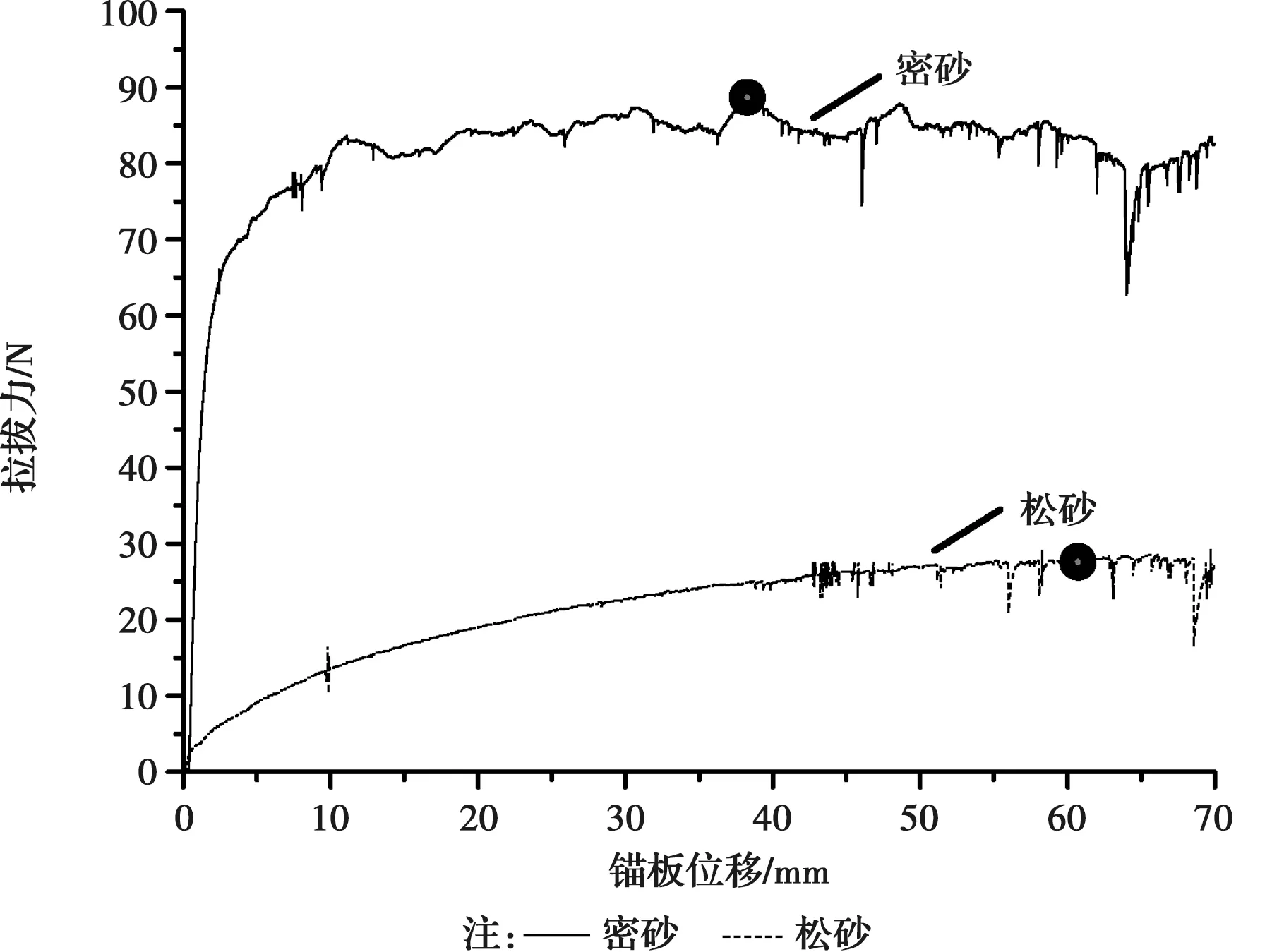
图3 H/D=3时砂土地基中锚板拉拔力与位移关系曲线

4.2 锚板拉拔时的位移场分析

在锚板上拔时，使用相机对锚板上拔过程进行实时拍摄，运用PIV技术对两幅图像进行相对位移计算，锚板周围土体的位移场分布可直观的反应砂土地基的破坏面。图4为埋深比H/D=1、3时锚板分别在松砂和细砂中土体位移场的计算结果。由图4可发现，当土体密实度及锚板埋深不同时，对锚板周围土体变形影响较大，且破坏面形态均不相同，具体表现：

1)当砂土地基浅埋(H/D=1)时，从位移场中可看出，松砂地基中锚板上部土体位移较小，破坏面呈现类似图1的柱状破坏面。而密砂地基中锚板上部土体位移变化明显，土体位移由锚板边缘向地表逐渐呈向外倾斜状增大，形成一个倒椎体形的影响区，破坏面与垂直面左右两侧的夹角分别约为14°和15°，破坏面基本对称且呈现为倒椎体。

2)当砂土地基深埋(H/D=3)时，松砂地基中锚板上部土体位移发生在地基内部，破坏面由锚板边缘向地表延伸，但未达到地基表面，由H/D=1时的呈现柱形影响区逐渐转变为灯泡形的影响区，破坏面所包围的区域范围约是锚板直径的1.5倍。同时，该影响区有压实作用，在锚板下部形成梯形空洞，但锚板上部地表并未出现隆起抬升现象，这表明，在松砂地基中锚板的拉拔过程也是松砂压密的过程。而密砂地基中锚板上部土体位移较大，破坏面与垂直面左右两侧夹角分别约为23°和17°，形状为由锚板边缘延伸至地表且呈曲线向外逐渐增大，类似于图1中的曲面破坏。

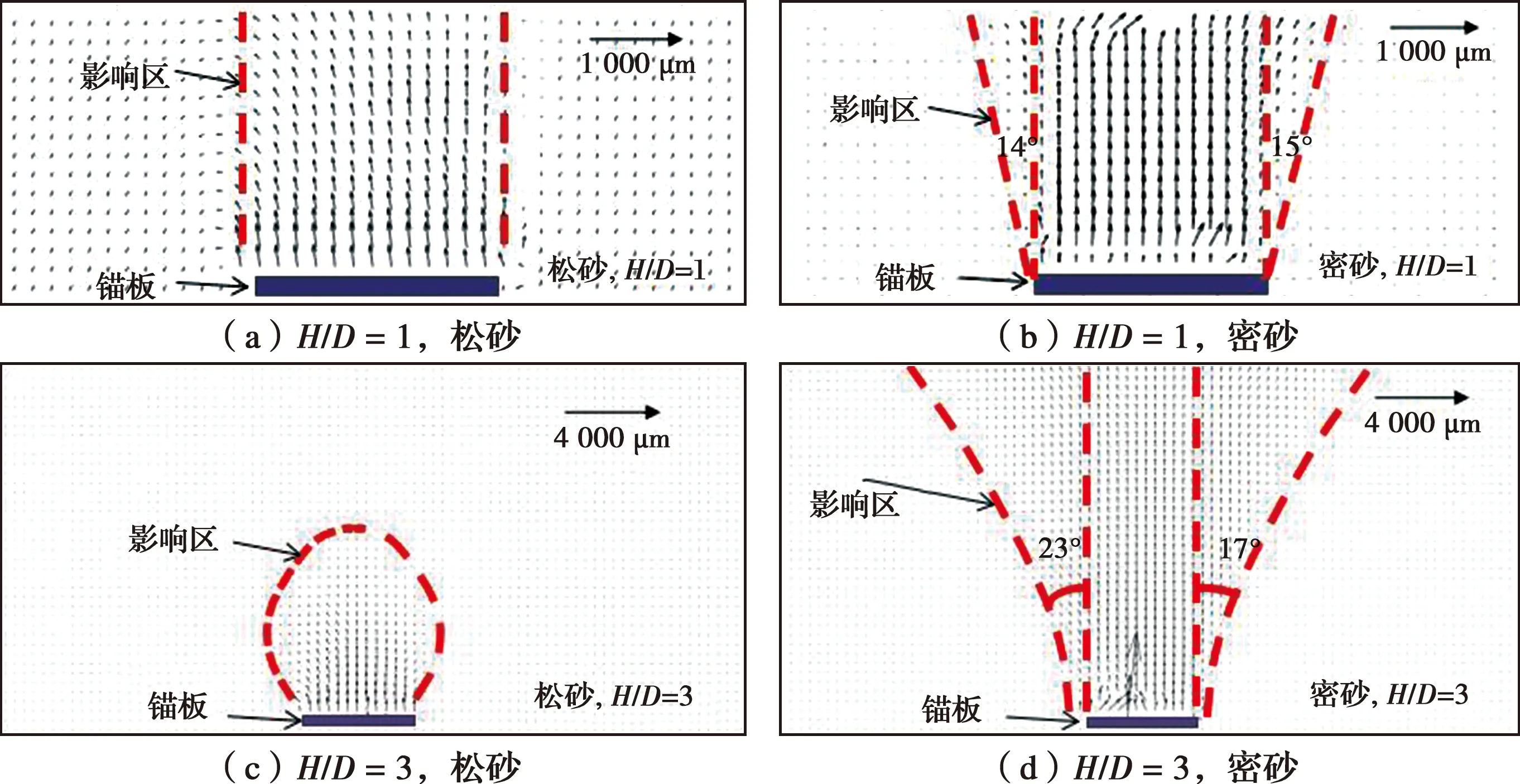
图4 锚板破坏时周围土体位移矢量图

Liu等[16]开展了类似研究，其结果如图5所示。对比发现，相似试验条件下，H/D=1时，松砂、密砂地基中的破坏面分布呈圆柱形和倒锥体，笔者试验结果与其基本一致。但H/D=3时，松砂地基内破坏面在锚板上部形成的灯泡状影响区，其影响区范围约是锚板直径的2倍，在密砂地基中破坏面影响区呈U型，而笔者所得松砂地基中影响区范围约是锚板直径的1.5倍，密砂地基中破坏面呈曲线型。形成这一差异的原因可能是因为试验采用的松砂、密砂密度并不一致，笔者所用松砂和密砂相对密实度为14.8%和76.2%，而Liu等所用松砂和密砂相对密实度为27%～47%和71%～85%。此外，试验发现由土体位移场得到的土体破坏面与图1中土体中锚板破坏模式较为一致。

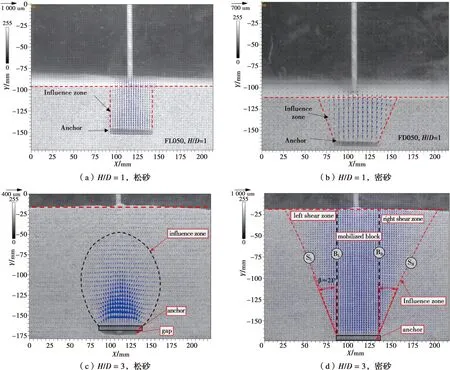
图5 锚板破坏时周围土体位移矢量图[16]

4.3 锚板拉拔时的应变场分析

土体破坏通常是剪切破坏，由最大剪应变值所在点可大致确定破坏带[16]。研究发现，土体密度和锚板埋深比对土体的剪切破坏模式均有影响，试验中由剪切应变场可近似得到土体的破坏面，图6为浅埋和深埋时松砂、密砂地基中剪切应变随锚板拉拔时的最终发展状态分布云图。

1)图6(a)、(b)为H/D=1时，松砂、密砂地基的最终剪切应变场。在松砂地基中，剪切应变场中形成的两条剪切带，由锚板边缘向地表延伸，二者形成锥形破坏面，如图6(a)所示。左右两侧剪切带大致对称，左侧破坏面与水平面的夹角为63°，约为45°+φ/2，其中φ是砂土的内摩擦角。

在密砂地基中，剪切应变场中的两条剪切带由锚板边缘产生并发生倾斜，可能是因为试验过程中砂土为人工分层填埋压密，锚板左侧上方土体压密不均，相比右侧土体疏松，锚板上方两侧土体剪切速率不同，在拉拔锚板时锚板发生向右侧倾斜，由图4(b)密砂位移场矢量图可以看出，锚板上方土体有向右位移的迹象。同时，试验中不可避免地会有些砂粒沿半圆形锚板表面滑落，及图像处理的计算误差，造成破坏面左右不对称，左侧破坏面出现向右倾斜，如图6(b)所示。右侧剪切带与垂直面夹角约为11°，约为φ/4。

2)图6(c)和(d)为H/D=3时，松砂、密砂地基的最终剪切应变场。在松砂地基中，剪切应变区域沿着锚板上部边缘发展，达到峰值拉拔力时最终发展情形如图6(c)所示，破坏面与位移场分析中类似，为灯泡形的影响区，影响区包围的区域范围约是锚板直径的1.5倍，该影响区中的砂土此时的塑性行为主要体现为砂土受到压密。锚板边缘两侧产生的剪切带形成锥形破坏面，剪切带与水平面的夹角为61°，约为45°+φ/2。

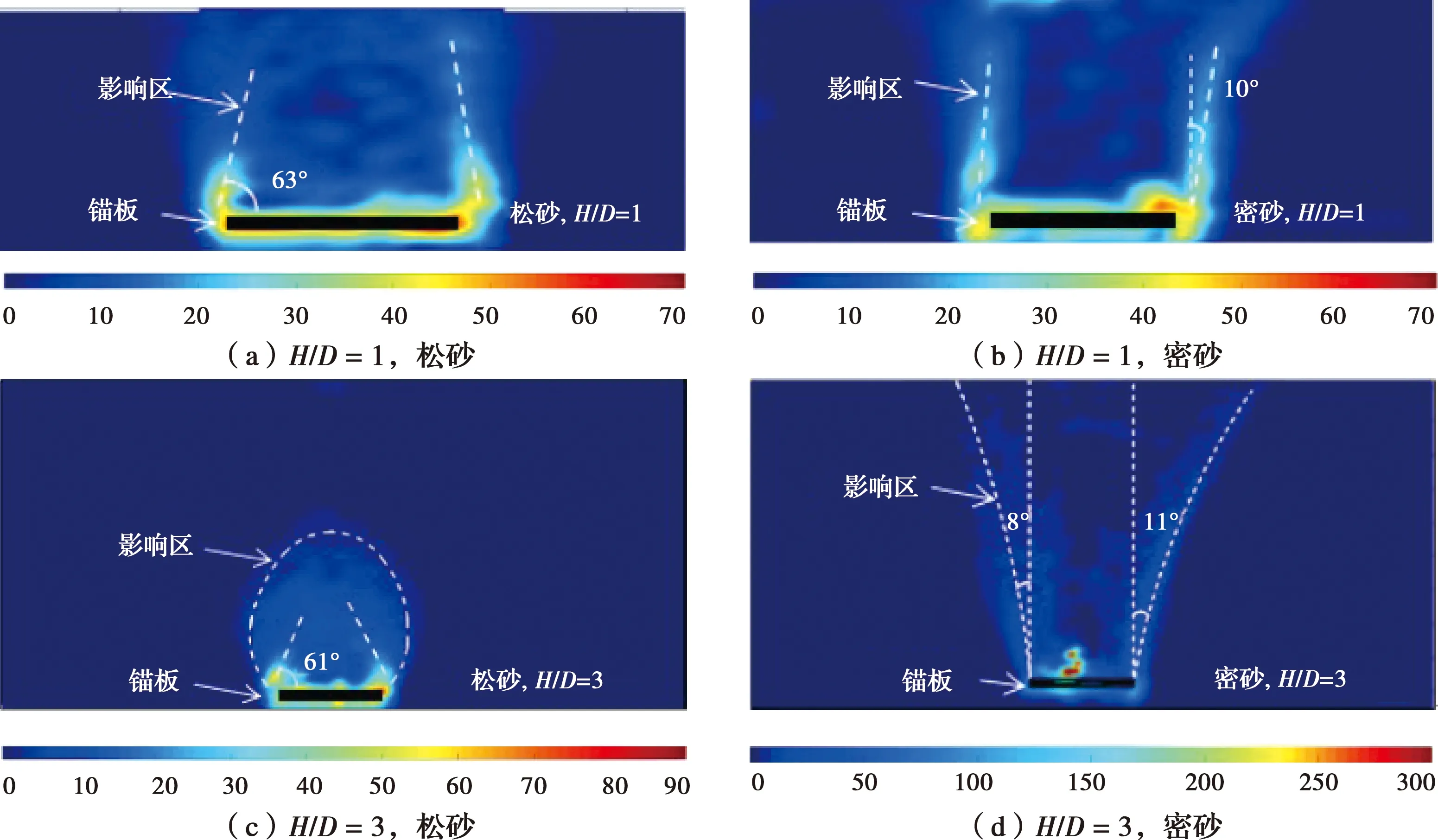
图6 地基中剪应变最终云图

在密砂地基中，剪切应变场中锚板边缘产生两条明显的剪切带，从锚板边缘延伸至地基表面，如图6(d)所示，破坏面与位移场分析中一致，为曲面破坏。左右两侧剪切带与垂直方向的夹角分布约为8°和11°，约为φ/4。

Liu等[16]的研究中，分细砂和粗砂对剪切应变场的影响，但粒径大小的不同对土体中锚板的破坏模式的影响可忽略不计。细砂和粗砂在松砂地基中破坏面与水平面的夹角分别为71°或77°，本研究中夹角为61°，均约为45°+φ/2；细砂和粗砂在密砂地基中破坏面与垂直面的夹角分别为10°和7°，夹角为11°，均约为φ/4，研究结果与Liu等的研究结果基本一致。

此外，研究过程中还发现，在松砂地基中剪切带与水平面夹角与其他研究者所得的结果[1,16]基本一致，但在密砂地基中，破坏面与垂直面夹角与Ilamparuthi等[1]得出的φ/2相比要小些。这是因为笔者这一角度测量基于剪切应变场，而其他研究者的角度测量基于土体位移场，因此造成了差异，但前文中密砂的破坏面与垂直面夹角约为φ/2。剪切应变场中的破坏面被认为更接近真实破坏面，这也说明了大多数基于位移场假定的破坏面高估了锚板的抗拔能力[16]。

5 结论

基于粒子图像测速技术，对锚板拉拔过程中锚板周围土体的位移场和应变场进行了分析，得到不同地基土密实度和锚板埋深条件下锚板周围土体的变形及破坏模式，结论如下：

1)当锚板浅埋(H/D=1)时，松砂地基中破坏面延伸至地表，破坏面呈柱状体，两条剪切带形成锥形破坏面，剪切带与水平面的夹角约为45°+φ/2。而密砂地基中破坏面呈倒锥体，剪切带由锚板边缘产生并发生倾斜，剪切带与垂直面形成的夹角约为1/4φ。

2)当锚板深埋(H/D=3)时，松砂地基中破坏面未到达地表，在锚板上部形成灯泡形的影响区。该影响区有压实作用，且锚板边缘产生的剪切带形成锥形破坏面，剪切带与水平面的夹角约为45°+φ/2。而密砂地基中两条剪切带由锚板边缘产生延伸至地表，破坏面呈曲面，剪切带与垂直方向的夹角约为φ/4。

3)在松砂地基中，剪切带与水平面的夹角约为45°+φ/2，而在密砂地基中，剪切应变带与垂直面夹角为φ/4。不论是松砂还是密砂地基，剪切带所形成的夹角均与砂土地基中锚板的埋置深度无关。