一种旋转导弹锥形运动稳定性分析方法研究*

孔寒雪，蒋虎超，朱雯雯，张晓峰，朱成成

(上海航天控制技术研究所·上海·201109)

0 引 言

旋转是战术导弹和制导弹箭所采用的一种重要体制。随着科学技术的高速发展和未来战场环境的日益恶化，现代武器系统正朝着多样化、智能化、协同一体化和低成本的方向发展[1-2]。采用旋转体制的导弹由于其特有的一些优点，在制导武器系统中具有巨大的发展潜力和应用前景[3]。旋转导弹多为近程、低空、快速反应的防空导弹，主要拦截来自低空和超低空的空中威胁，为超近程防空武器装备。旋转导弹的主要特点是：在飞行过程中，绕其纵轴低速自旋；使用单通道控制，控制系统简单，导弹只需一对操纵机构，即可获得俯仰和偏航方向的控制力，实现导弹在空间做任意方向的运动[4]。但在旋转导弹飞行过程中，将产生马格努斯效应和陀螺效应，使旋转导弹俯仰和偏航通道具有气动交联、惯性交联和控制交联，使旋转弹具有特殊的动力学特性。这种特性表现为弹体除了绕自身的纵轴旋转外，还会绕其速度矢量轴做周期式的圆形运动，也就是锥形运动[5]。这种锥形运动会产生如附加的马格努斯效应、陀螺效应导致的通道间严重耦合等，将影响导弹的控制和制导精度，如果锥形运动发散，甚至可能造成弹体飞行失稳，导致飞行任务失败[6]。对于锥形运动的形成原因、稳定条件等国内外已进行了一些研究。Peterson等首先分析了导致锥形运动的可能因素：包括发射的不确定因素、初始扰动、马格努斯力和力矩等[7]；Nicolaides等通过理论推导和风洞实验，证明了旋转诱导产生的面外力和面外力矩是产生锥形运动的直接原因[8]；Shi等从刚体运动和弹性形变耦合的角度分析了耦合对锥形运动的影响[9]；Ji等基于速度控制规律设计，通过建立关于速度的一阶近似模型，研究了锥形运动对飞行器的影响[10]；Yan等基于章动理论对圆锥运动稳定性进行了分析[11]；任天荣等基于旋转弹的变质量陀螺方程，对旋转弹产生锥形运动的条件进行分析探讨[12]；颉凯平等通过对锥形运动稳定性的理论分析和仿真计算，得到了确保火箭弹稳定飞行的舵翼面安装误差及发动机推力偏心指标要求[13]。

本文将以旋转导弹为研究对象，对锥形运动进行动力学建模，通过劳斯定理，分析锥形运动稳定的条件和角运动特性，并通过仿真分析旋转导弹转速和速度对锥形运动稳定性的影响，为设计相应的控制策略抑制导弹的锥形运动提供理论基础。

1 锥形运动动力学建模

锥形运动可以由弹体系oy1轴、oz1轴的速度和绕着两个轴的角速度描述，分别以弹体坐标系oy1、oz1的速度Vy、Vz，角速度分量ωy、ωz为状态变量，建立动力学方程如式(1)所示[14]

(1)

式(1)中，θ、φ为弹体的俯仰角和滚转角，Vx、Vy、Vz为导弹速度在弹体系各轴上的分量，ωx、ωy、ωz为导弹角速度在弹体系各轴上的分量，My、Mz分别为俯仰力矩和偏航力矩，Fy、Fz为气动力在弹体系oy1轴、oz1轴的合力，Jx、Jy、Jz为导弹对弹体系各轴的转动惯量。

可以将气动力转换至弹体坐标系下进行计算，如式(2)所示

(2)

式(2)中X、Y、Z为速度坐标系下的三轴气动力，X为阻力，Y为升力，Z为侧向力；α、β为攻角和侧滑角。

由于所研究的动态稳定性问题是在锥形运动的章动角是一个小值的前提下进行的，所以可将原来的系统用一个线性系统在稳定点附近加以近似。通常都是基于小角度假设和系数固化假设，这些假设包括：

(1) 旋转弹质心速度矢量沿弹体纵轴的分量Vx的数值很大，接近于质心前进速度V

(3)

(2) 小角度假设，例如俯仰角比较小，所以进行如下线性化

sinθ≈θcosθ≈1

(4)

(3) 攻角和侧滑角可以近似表示为

α≈Vy/Vβ≈Vz/V

(5)

(4) 弹体速度、转速、质量以及空气动力系数在小段时间内保持不变；

(5) 角速度、速度等矢量的横向分量比较小，将横向分量之间的乘积项忽略。

基于以上的假设，可以得到一个四阶的动力学矩阵如式(6)

(6)

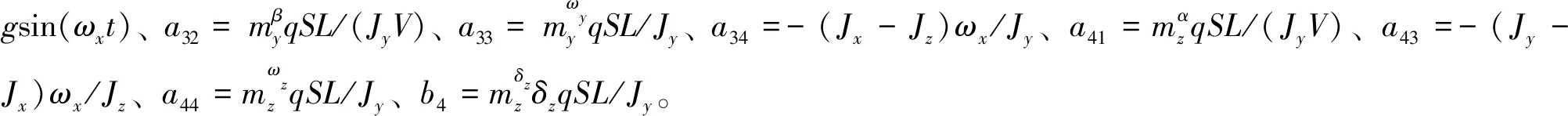
2 锥形运动稳定性分析

一个动力学系统稳定的充要条件是系统特征方程的根均具有负实部，将式(6)中的动力学方程可以写为一般形式如式(7)

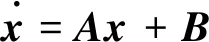
(7)

式中，状态变量x=[Vy,Vz,ωy,ωz]T；A为系统矩阵，决定系统的稳定性，用式(8)表示

(8)

根据劳斯判据可知，如果一个系统是稳定的，则劳斯判定式的第一列都应该为正数，即特征方程所有的根均位于根平面的左半平面[15]。

所以要判定系统的稳定性，首先要得到系统的特征方程。将系统的状态矩阵代入式(9)

|sI-A|=0

(9)

可得到系统的特征方程如式(10)所示

Δ(s)=f4s4+f3s3+f2s2+f1s+f0

(10)

式中

(11)

根据劳斯判据，可以得到系统稳定的充要条件为

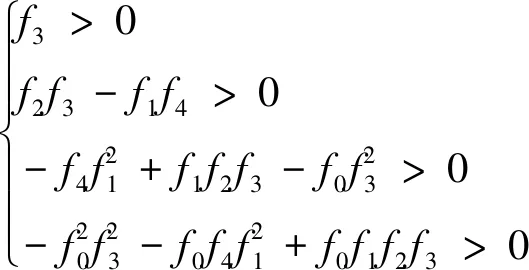
(12)

从式(6)和式(12)可以看到，决定锥形运动稳定性的不等式组其系数由导弹的飞行状态(高度、速度)、相关气动参数和弹体自旋角速度决定。所以通过代入导弹在不同状态下的弹体气动参数，可以得到旋转导弹稳定性的边界条件对不同参数的要求。

3 仿真验证

在弹体外形已经确定的情况下，导弹的飞行状态决定了弹体在此状态下的气动特性，所以在分析锥形运动的稳定时，主要对飞行速度和弹旋速度对锥形运动稳定性的影响进行分析。

对旋转导弹的稳定性判据进行仿真验证。首先对其在相同转速，不同速度下的锥形运动进行仿真，通过绘制攻角和侧滑角在半弹体坐标系下的运动曲线，来看锥形运动对弹体角运动的影响。由于仿真在弹体坐标系下完成，需要对弹体系下的攻角和侧滑角进行转换，其计算方法如式(13)所示

(13)

式中，α4和β4分别为半弹体下的攻角和侧滑角，α1和β1分别为弹体系下的攻角和侧滑角。假设弹体的自旋速度为15r/s，分别对不同速度下的导弹进行仿真，设定初始的半弹体下攻角和侧滑角扰动为2.5°，可以得到此时角运动曲线如图1所示。

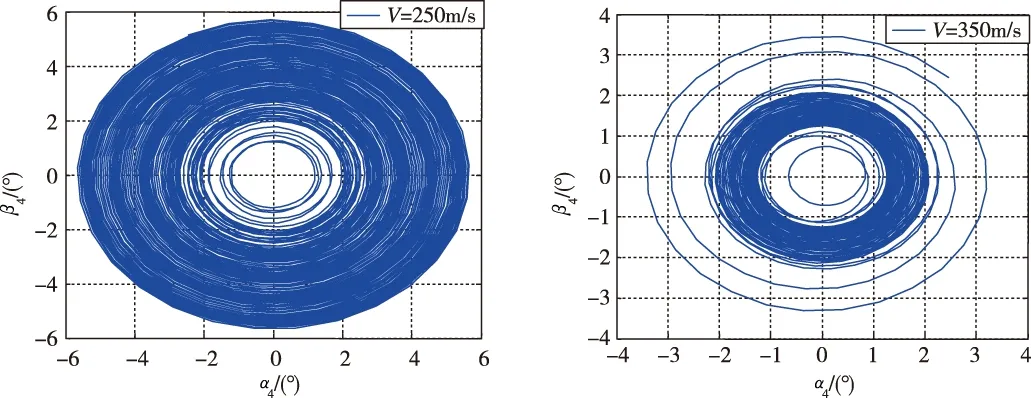
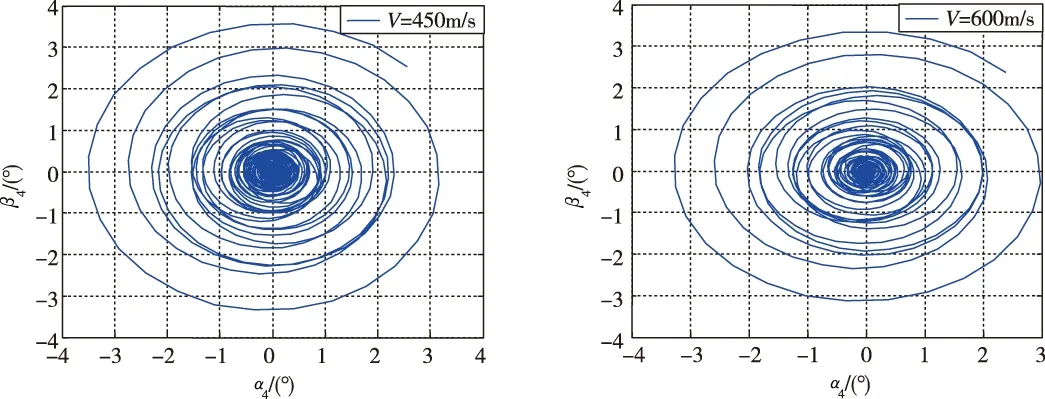
图1 不同速度下的旋转导弹角运动曲线Fig.1 Angular motion curves of rotating missile at different speed

从图1中可以看出，随着速度的增大，旋转导弹锥形运动的稳定性越强，在速度为250m/s的时候，锥形运动发散，速度为350m/s的时候，锥形运动临界稳定，速度为450m/s和600m/s，锥形运动有着良好的稳定性。

下面对旋转导弹在某一飞行状态下，不同转速下的锥形运动进行仿真，假设某一旋转导弹在高度为1500m、速度450m/s的条件下的弹体参数和气动参数如表1和表2所示。

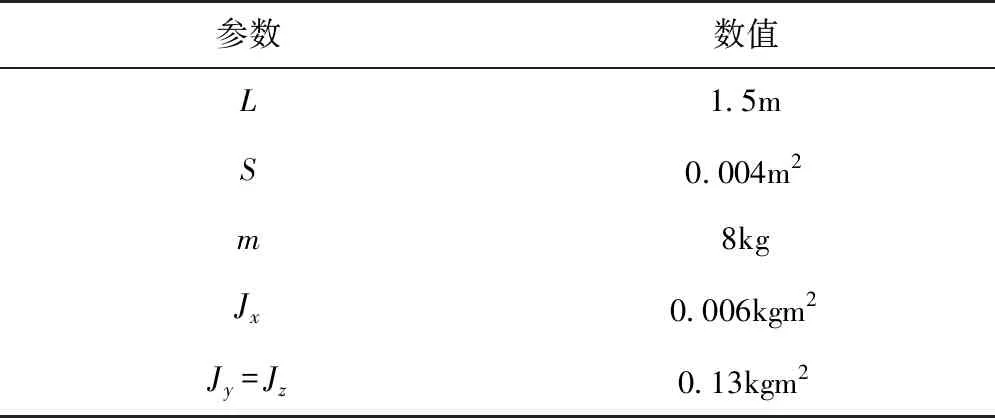
表1 弹体参数Tab.1 Projectile body parameters

表2 气动参数Tab.2 Aerodynamic parameters

将表1和表2的数据代入式(6)、(7)、(10)，同时解式(11)的不等式组，可以得到此状态导弹的稳定边界条件为：

0<ωx<26.80r/s

下面分别在弹体不同转速的情况下对其角运动特性进行仿真，其仿真结果如图2所示。

从图2中可以看出，导弹在6r/s和15r/s的转速下运动，其锥形运动收敛，且转速较低，收敛较快，在28r/s时略超出稳定边界，锥形运动未收敛，而在30r/s锥形运动明显发散。

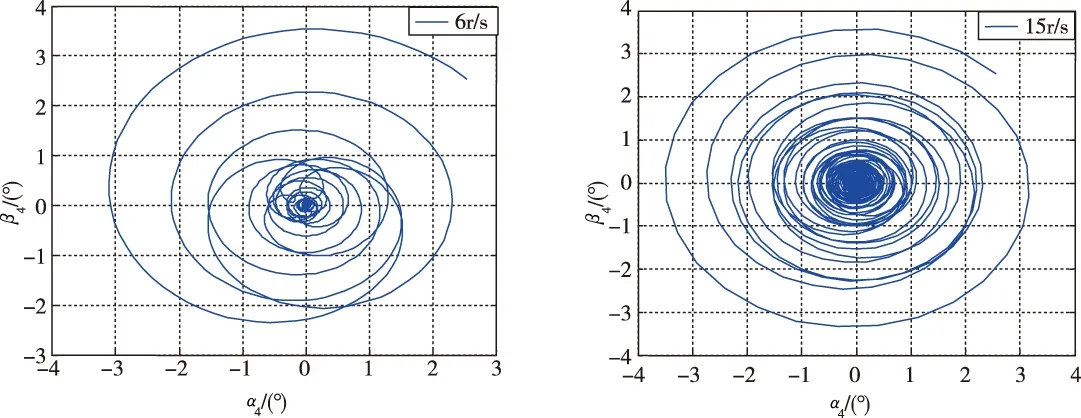
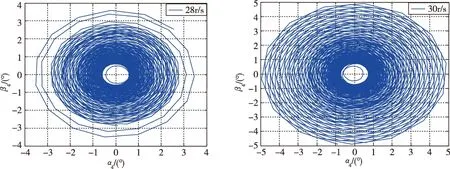
图2 旋转导弹不同转速下的角运动曲线Fig.2 Angular motion curve of rotating missile at different rotational speed

由于在旋转导弹飞行过程中，其转速与速度常常存在一定的对应性，当导弹到达一定飞行速度的同时，导弹也达到一定的转速，将导弹不同速度下的气动参数代入稳定性判据可以得到导弹在不同速度下对转速边界的要求如表3所示。

表3 不同速度下的稳定性边界Tab.3 Stability boundaries at different speed

由表3可知，当导弹达到相应的飞行速度时，要保持导弹的锥形运动稳定，其转速也应在相应的范围内。

4 结 论

本文通过对锥形运动的关联状态变量进行动力学建模，得到了只含有弹体自旋速度、气动参数、飞行状态等变量的状态方程。通过劳斯定理进行分析，得到了关于弹体自旋速度的不等式组，从而分析了影响旋转导弹锥形运动稳定的因素。除了弹体自身的气动外形、飞行状态外，旋转导弹的转速也是影响其锥形运动稳定性的关键因素。通过分析，提出了一种基于劳斯定理的旋转导弹锥形运动稳定性分析方法。在旋转导弹的飞行状态确定后，通过推导不等式组确定了旋转导弹的稳定性边界，并通过仿真对旋转导弹锥形运动稳定性进行了分析，验证了稳定性条件的正确性。通过该方法对旋转导弹锥形运动进行稳定性分析，对旋转导弹总体设计及制导控制系统设计具有一定的实际意义。