多梁复合结构的动力学建模及全局解析振型分析*

王凤祥，郝淑英，胡文华

(1.天津理工大学 机械工程学院天津市先进机电系统设计与智能控制重点实验室·天津·300384;2.天津理工大学 机电工程国家级实验教学示范中心 ·天津·300384)

0 引 言

多梁复合结构广泛应用于航空航天工程等领域，例如：空间机械手、卫星天线、国际空间站结构[1]、能量采集器[2]。图1中的空间站机械手[3]和工业机械臂具有多梁复合结构的典型特征。深入研究这些结构的动力学特性是所在系统进行参数设计和运动控制的关键[4]。

(a)空间站机械手

(b)工业机械臂图1 典型多梁复合结构Fig.1 The typical multi-beam composite structures

常见的多梁复合结构有L型梁、T型梁、Z型梁和门型梁，国内外许多学者对这些结构的平面运动模型的频率或振型进行了研究。Balachandran和Nayfeh[5]利用拉格朗日方程对L型结构的平面弯曲振动进行了动力学分析。Warminski等人[6]研究了两个正交方向上具有不同柔度的L型梁的振型相互作用。Narayanan等人[7]研究了三自由度T型结构在简谐激励下的非线性动力学响应。Uddin等人[8]指出T型压电悬臂梁能够将环境振动能量转化为生物医学设备的电能。Wei等人[9]对带末端质量的L型梁在不同全局模态下的动态响应进行了研究。Chen等人[10]通过三次多项式近似地求出了L型梁的挠度[11-13]。Erturk等人[14]设计了L型压电能量采集器，指出该型采集器具有较宽的能量采集频带。三梁结构也引起了研究者的广泛关注[15-17]。Filipich等人[18]研究了附有扭簧和集中质量的门型框架的自由振动。Pan等人[19]讨论了五种典型的门型框架屈曲问题。此外，工程中也常用到折叠结构，如机械臂和旋臂起重机。Guan和Zhu[20]指出Z型热微致动器与传统V型致动器相比有一定的优势。Mardanpour和Hodges[21]将机翼等效成Z型结构研究其变形过程。在结构的动力学研究和控制中，结构振型的精度至关重要。Kim和Yoo[22]研究了多参考系对折角旋转梁结构振型分析收敛性和准确性的影响。Tripathi和Bajaj[23]用有限元法计算了几种多梁复合结构的振型，并且分析了振型误差。Wei等人[24]建立了非线性节点连接的多梁结构的动力学模型。Zhang等人[25]用实验方法定性地验证了所获得的Z型梁的解析振型。梁结构的非平面运动控制方程中通常存在较多耦合变量，因此，其非平面动力学特性比平面动力学特性更为复杂。Ho等人[26]分析了简支梁的弯曲和纵向变形。Silva和Glynn[27-28]建立了强迫振动下梁的非平面运动控制方程。Zhang[29]分析了悬臂梁结构的非平面振动特性。Georgiades等人[30]研究了L型梁的非平面线性振型。

上述文献在多梁复合结构的平面或非平面运动模型上做了很多工作，但很少涉及解析振型的定量验证。本文利用哈密顿原理建立多梁复合结构的动力学模型，得出运动控制方程及其边界条件，给出了多梁复合结构的线性频率和全局解析振型的求解方法，提出了在数值结果的基础上通过MAC和频率对比对全局解析振型进行了定量验证的方法，以L型梁和Z型梁为例说明了求解及验证全局解析振型的有效性。本文提出的一种求解多梁复合结构的全局解析振型并进行定量验证的方法，对相关工程应用中多梁复合结构的参数设计和运动控制具有指导意义。

1 理论建模

1.1 位置向量

多梁复合结构是指多根直梁组成的复合结构，常见的形式有L型梁、V型梁、Z型梁以及门型梁等结构。图2中，(a)为L型梁结构，(b)为Z型梁结构，坐标OXYZ表示惯性坐标，oixiyizi是结构中第i部分的局部坐标。

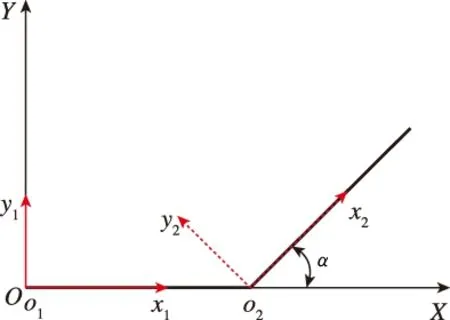
(a)L型梁

(b)Z型梁图2 多梁复合结构示意图Fig.2 Scheme of multi-beam composite structures

多梁复合结构中各部分的位置向量可表示为

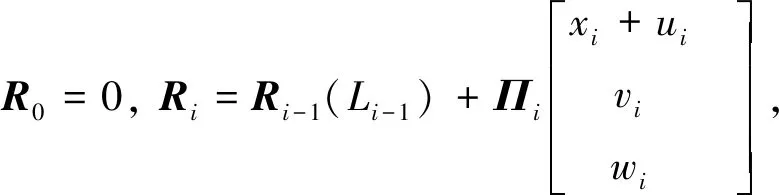
(1)

式中：Πi见附录A；ui、vi、wi分别表示多梁复合结构中各部分在xi，yi和zi轴方向的位移；Li是第i部分的长度。n是复合梁结构包含的直梁个数。如果只考虑复合梁结构在平面内位移，公式(1)可简化为平面运动模型。当n=2时，公式(1)可用于描述V型梁和L型梁；当n=3时，公式(1)可用于描述Z型梁和门型梁。

1.2 系统能量

多梁复合结构中各部分的动能可表示为

Ti=

i∈{1,2,…,n}

(2)

式中：符号| |表示对矢量取模，ρi是多梁复合结构中第i部分的密度；Jix、Jiy、Jiz分别表示沿x、y、z方向的主质量惯性矩；ωix、ωiy和ωiz分别表示沿x、y、z方向的角速度；Ai是横截面积；Kix是扭转刚度；Kiy和Kiz分别表示沿y、z方向的弯曲刚度；κix、κiy、κiz分别表示沿x、y、z方向的曲率。

多梁复合结构中各部分的势能可表示为

(3)

式中σi和εi分别表示多梁复合结构中第i部分的应力和应变。

1.3 控制方程及边界条件

将系统动能和势能代入哈密顿方程，有

(4)

式中：Hi是为方便和简化计算而引入的符号。

通过变分计算，得出多梁复合结构的运动控制方程及边界条件如下

(5)

(6)

式中：i∈{1,2,…,n}，γi∈{ui,vi,wi,θi},θi表示多梁复合结构中第i部分绕各自xi轴的扭转角度，单撇号表示对xi求一次偏导数，双撇号表示对xi求两次偏导数。

2 全局解析振型

2.1 理论分析

对小幅振动，可以忽略式(5)中的非线性项，得到多梁复合结构的线性运动控制方程如下

(7)

(8)

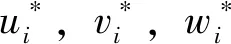
对式(7)、(8)中的变量进行变量分离，可以得到

(9)

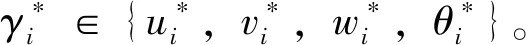
根据Georgiades等人[28]的研究，整个结构的运动是同步的。因此

(10)

将式(9)、(10)代入式(7)、(8)可以得到如下振型

(11)

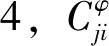
2.2 数值分析

本节以平面运动模型说明利用有限元法分析多梁复合结构的振型和频率。令结构中每个单元包含两个节点，每个节点具有三个自由度。例如，第k个单元的局部位移用第ζ个节点和第η个节点定义并表示为

(12)

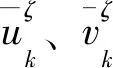
令长度为lk的第k个元素的形函数Nk为

(13)

(14)

(15)

为了获得质量和刚度的总矩阵，引入定位矩阵Lk和全局广义坐标p：

(16)

(17)

利用式(16)和(17)将每个节点的运动δk表示为

δk=Lkp

(18)

将单元的动能和势能代入到哈密顿方程：

(19)

通过变分计算并简化式(19)，得到

(20)

式中：M和K分别由式(21)和(22)表示

(21)

(22)

给定多梁复合结构的材料和几何参数，由式(20)可以计算出结构的线性频率和数值振型。

2.3 分析实例

2.3.1 L型梁

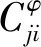
图3 L型梁的全局解析振型Fig.3 Global analytical modes of L-shaped beams

2.3.2 Z型梁

本节以Z型梁为例说明多梁复合结构的全局解析振型的定量和定性验证方法。令Z型梁一端固定一端自由，其几何和材料参数为：Ei=69GPa，ρi=2730(kg·m-3)，μi=0.33，Li=0.1m，bi=1.2×10-2m，hi=1×10-3m，i={1，2,3}，基于式(11)和式(20)可以求解出结构的线性频率。

图4给出了Z型梁的基于式(11)和式(20)获得的前三阶频率之间的相对误差。图中，f表示频率，上标T是解析结果，上标N是数值结果，下标是频率的阶数。从图中可以看出，解析频率与数值频率最大相对误差在±0.001以内，这表明两种结果具有良好的一致性。

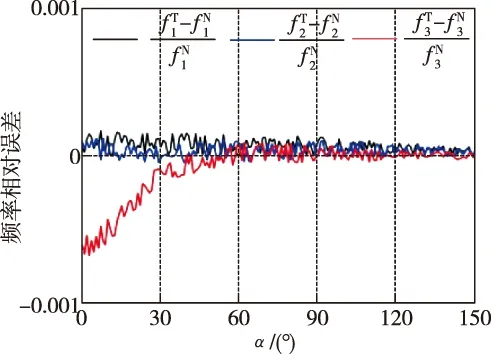
图4 Z型梁的前三阶频率相对误差Fig.4 The relative errors of the first three order frequencies of a Z-shaped beam

图5 Z型梁的前四阶解析振型Fig.5 The first four mode shapes of Z-shaped beams

图6 前五阶振型的MACFig.6 MAC of the first five order mode shapes

图7(a)所示的实验系统通常用来获取多梁复合结构的频率和振型。信号发生器输出激励信号经过功率放大器后输出到激振器，激振器振动多梁复合结构，数据采集器和传感器检测并记录结构的响应信号。图7(b)是Z型梁的实验现场图片。图中，铝合金Z型梁安装在激振器上，应变片贴在Z型梁的固定端，非接触位移传感器放置在Z型梁的侧面。应变片和非接触位移传感器分别用来测量结构的面内外位移。

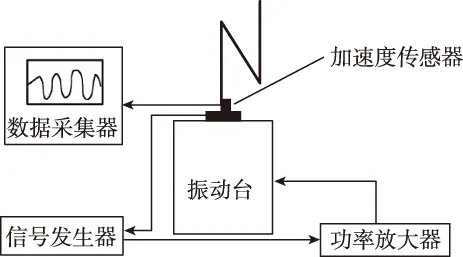
(a)实验系统示意图

图8给出了Z型梁在折叠角为60°时的振型。图8(a)、(b)和(c)分别是第一阶面内的解析振型、数值振型和实验振型，图8(d)、(e)和(f)分别是第一阶面外的解析振型、数值振型和实验振型。图中，解析振型由式(11)计算所得，数值振型由有限元软件ANSYS获得，实验振型由图7所示系统进行纯模态实验拍照所得。从图中可以看出，三种方式所获得的结果基本一致，这定量地验证了Z型梁全局解析振型的正确性。

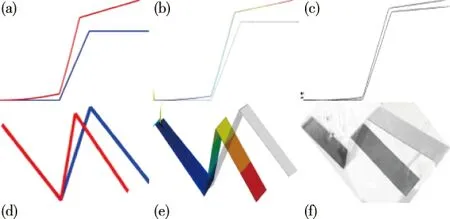
图8 Z型梁的第一阶面内外振型Fig.8 The first in-plane and out-of-plane order mode shapes of a Z-shaped beam

本节给出了关于多梁复合结构全局解析振型的求解方法，提出了基于数值分析以及实验分析的全局解析振型定量定性验证手段，以L型梁和Z型梁为例介绍了关于多梁复合结构的频率的解析方法和数值方法的误差分析，以及多梁复合结构全局解析振型的定性定量分析方法。

3 非线性模型

基于上一节中得到并验证的全局解析振型，利用伽辽金法，将公式(4)中各位移变量进行截断：

(23)

式中：qj是第j阶的无量纲广义坐标；φj是第j阶的振型；m是截断阶数；ε是小参数。

将式(23)代入式(4)，有

=0

(24)

引入无量纲时间：

(25)

将式(25)代入式(24)，得到

(26)

考虑系统受小幅激励情况，有

(27)

将式(27)代入式(26)，考虑阻尼，得到无量纲的m自由度非线性系统：

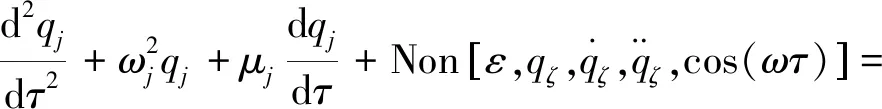
(28)

式中：ωj表示第j阶的无量纲频率；μj表示第j阶的无量纲阻尼系数；Non表示非线性项；ζ∈{1,2,…,m}；Fj表示第j阶的无量纲外激励幅值分量；ω表示无量纲外激励频率。

本节利用伽辽金方法对连续系统进行截断，得到了系统的常微分运动控制方程，可为多梁复合结构的非线性动力学特性研究提供基础。显然，式(28)中各参数与式(23)中引入的全局解析振型φj有密切关系，因此，解析振型的准确性对系统非线性动力学特性分析有很大影响。

4 结 论

本文给出了多梁复合结构的位移场的一般表达式，通过哈密顿原理推导出多梁复合结构的运动控制方程及其边界条件的通式，给出了多梁复合结构的全局解析振型的一般求解过程，并提出了基于数值分析和实验分析对多梁复合结构的全局解析振型进行定性定量验证的方法，以L型梁和Z型梁为例利用频率误差分析、振型的定性比较以及定量MAC分析说明了本文提出的全局解析振型求解验证方法的正确性，进一步利用伽辽金方法和全局解析振型对多梁复合结构进行截断，得到了其对应离散系统的一般形式，为后续研究非线性动力学特性提供了理论基础。

解析振型的准确性对利用伽辽金方法截断系统进而进行非线性动力学特性分析有很大影响。本文提出的全局解析振型求解验证方法，可以提高基于振型对原系统进行截断得到的非线性离散系统的准确性，对工程中多梁复合结构非线性动力学响应的参数影响规律研究有重要意义，该方法也可以拓展应用于对更一般形式的复合结构的动力学研究。

(A1)

(A2)

(A3)

附录B

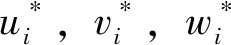
(B1)

(B2)

(B3)

(B4)

(B5)

(B6)

(B7)

(B8)

附录C

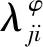
(C1)

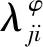
(C2)

(C3)

式中：ωφ表示与振型φ对应的频率。