基于异构传感器网络的随机系统节点协同方法研究

卞 秀 运

(江西应用科技学院 江西 南昌 330100)

0 引 言

随着电子科技等技术的飞速发展，传感器节点具有强大的数据处理功能，制造成本低，体积小，因此，无线传感器网络也得到广泛的发展与应用[1]。传感器网络通过节点相互通信、相互协同工作，从不同的角度获取数据，使得获取的数据具有较高的正确率和可信度[2]。而节点的死亡退出和添加，或者节点移动等都会导致节点的邻居集发生变化，改变了网络的拓扑结构，通信图变为动态，进而造成计算复杂和瞬态的不稳定[3]。无线传感器网络应用的另一个问题是通信延迟，当网络中出现时间延迟，节点则需通过其他节点评估其相邻节点的当前数据，容易造成网络的不稳定和振荡等问题[4]。

在一般的传感器网络中，通常采用集中式卡尔曼滤波器或分散式卡尔曼滤波器进行估计，分散式卡尔曼滤波器估计没有用于数据融合和分析的中央单元，每个节点的估计类似于集中式卡尔曼滤波器[5]，而集中式卡尔曼滤波估计受到大型传感器网络中的限制，所有节点可能无法将其测量信息发送到中央单元。近年来，切换拓扑、通信延迟、丢失和噪声连接已用于分散估计[6]。

陈嵩等[7]采用粒子群优化算法，对无线传感网络通信延迟进行消除，通过能量消耗量找出节点死亡过程中网络延迟的变化规律，对无线传感网络的目标函数进行优化，并通过自适应策略达到快速消除通信延迟的目的。徐艮凤等[8]提出了一种无线传感器网络数据融合的算法，该算法将无线传感器网络节点分解成多个不均匀簇，并构建拓扑结构，以达到低延迟和低能耗的效果。任霞丽[9]提出了基于协同过滤的镜像误差修正定位算法(Correcting Localization Algorithm of mirror image error based on Cooperation Filtering，CLACF)，该算法通过相邻节点网络引入定位模型，通过过滤方法挑选出精确度高节点的位置信息，能有效地降低整个传感器网络的定位误差。Zhou等[10]研究了具有切换拓扑的连续线性时不变系统的分布式估计，文中假设网络具有状态一致的传感器，并且系统对于所有节点都是可观察的，然而，该估计方法不能适用于具有通信延迟和异构传感器的网络。而在随机线性时变系统中，极少有同时考虑切换拓扑和通信延迟的异构传感器网络的协同估计。

本文通过每个节点仅与其邻居通信，同时考虑通信延迟和切换拓扑，每个网络节点融合测量信息，并通过协同估计确定目标系统的状态。基于这种传感器网络的协同估计方法，提出了一种用于传感器网络协同估计的算法，对具有切换拓扑和连接延迟的传感器网络进行分散估计。该方法不需要整个目标系统的状态进行估计，允许网络具有不同测量矢量的异构传感器，且提高了估计精度。

1 问题定义

具有N个传感器网络和一个移动目标，目标与传感器连接表达式为g(t)=(N,εG(t))，其中G(t)为N×N相邻矩阵。在时间t时刻，如果第i个节点可以从第j个节点接收信息，则gij(t)=1，否则gij(t)=0。如果图是无向的，则节点i和j可以相互接收彼此的信息。时变目标的动态方程为状态空间形式，即：

ξ(t+1)=A(t)ξ(t)+B(t)w(t)

(1)

式中：ξ(t)为状态向量，w(t)为零均值高斯过程噪声，其方差为σ(t)。矩阵A(t)和B(t)分别为目标的给定状态转移矩阵和输入矩阵。在具有N个传感器的传感器网络中，第i个传感器的测量表示为：

yi(t)=Ci(t)ξ(t)+vi(t)i=1,2,…,N

(2)

式中：Ci(t)为状态观测增益矩阵，vi(t)为第i个传感器的零均值白高斯测量噪声，其方差为σi(t)。通常假设在时间t，传感器网络的第i个节点只访问由通信图确定的其相邻信息Ni(t)。通信图具有可变的拓扑结构，其切换不受设计者的影响。

2 协同估计算法

以τ(τ>0)表示传感器网络中的通信延迟，则在时间t-τ之前的测量数据为有效数据。在每个网络节点处计算该时间t-τ状态的协同估计，同时考虑到相邻节点的延迟信息，进行预测每个节点处时间t的系统状态，进而获得目标系统的动态估计。第i个传感器相邻测量值的矢量为：

(3)

第i个节点计算的延迟信息状态预测及其误差协方差矩阵定义为：

(4)

Pi(t|t-τ)=σ(ξ(t)-ξi(t|t-τ))

(5)

通过卡尔曼滤波器的预测关系可以确定第i个节点协同估计ξi(t-τ∣t-τ)。对于传感器网络的第i个节点，若ξi(t-τ∣t-τ)和Pi(t-τ|t-τ)已确定，则:

(6)

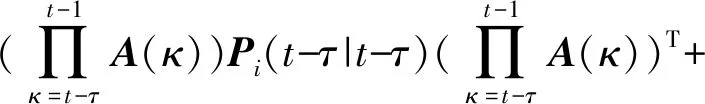
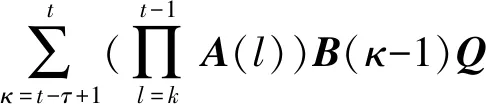
(7)

当i>j时，ξ(t)为:

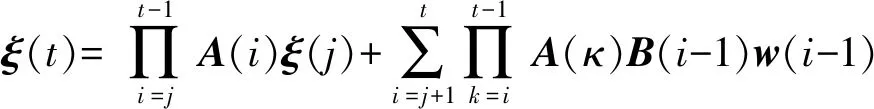
(8)

将式(8)代入式(4)，则对于j=t-τ，第i个节点的预测为:

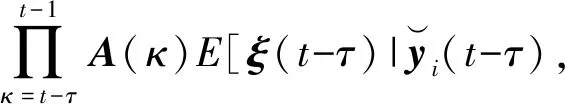
(9)

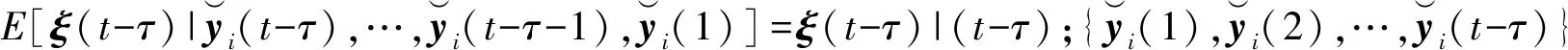
E[w(i-1)]=0

(10)

故，式(9)简化为:

(11)

将第i个节点预测误差定义为:

ξi(t|t-τ)=ξ(t)-ξi(t|t-τ)

(12)

将式(12)依次代入式(8)、式(11)和式(12)可得:

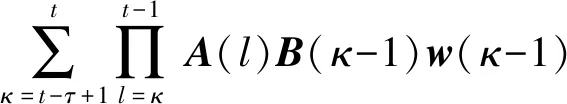
(13)

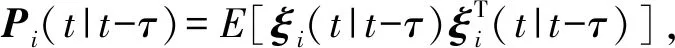
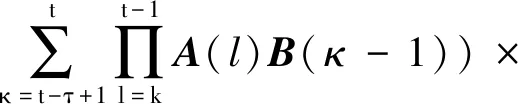
(14)

式中：E[ξ(t-τ)wT(j)]=0，j=t-τ，t-τ+1,…，t-1。因此，ξi(t-τ∣t-τ)可表示为：

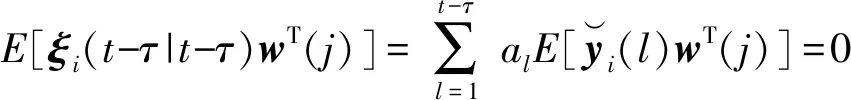
当j=t-1，t-2,…，t-τ，则:

E[ξi(t-τ|t-τ)wT(j)]=0

(16)

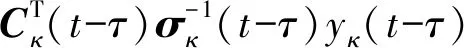
ξi(t-τ|t-τ)=Pi(t-τ|t-τ)(Pi-1(t-τ|t-τ-1)ξi(t-

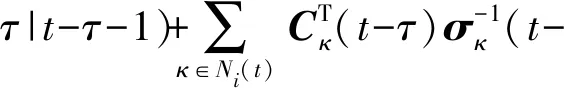
τ)yκ(t-τ))

(17)

Pi(t-τ|t-τ)=(Pi-1(t-τ|t-τ-1)+

(18)

在t时刻，第i个节点邻居的测量矢量(式(3))可表达为:

(19)

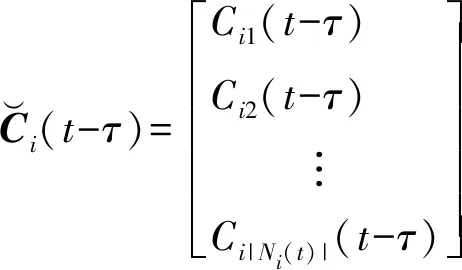
由于vi(t)是不相关的高斯白噪声，均值为零，且σi(t)的方差也为零，因此，vi(t)也是高斯分布，均值为零，方差为:

(20)

因此，卡尔曼滤波器的递归关系为:

ξi(t-τ|t-τ-1)=A(t-τ-1)ξi(t-τ-1|t-τ-1)

(21)

Pi(t-τ|t-τ-1)=A(t-τ-1)Pi(t-τ-1|t-τ-

1)AT(t-τ-1)+B(t-τ-

1)Q(t-τ-1)BT(t-τ-1)

(22)

ξi(t-τ|t-τ)=ξi(t-τ|t-τ-1)+Ki(t-

(23)

τ))Pi(t-τ|t-τ-1)

(24)

(25)

利用矩阵反演引理，式(23)和式(24)可写为:

ξi(t-τ|t-τ)=Pi(t-τ|t-τ)(Pi-1(t-τ|t-

τ-1)ξi(t-τ|t-τ-1)+

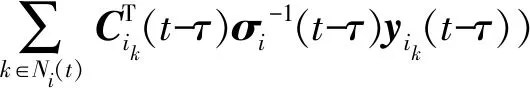
(26)

Pi(t-τ|t-τ)=(Pi-1(t-τ|t-τ-1)+

(27)

通过式(26)和式(27)可求解式(17)和式(18)。卡尔曼滤波器是具有最小方差的最优线性滤波器，考虑延迟τ和本地节点之间的信息交换，式(17)和式(18)是估计误差协方差意义上第i个节点的最优解。通过获得的结果，进而在传感器网络中具有通信延迟的协作估计获得在传感器网络中具有通信延迟的协作估计算法，在时间t处的连接拓扑即为g(t)。

第i个节点通过通信网络向其所有邻居发送消息，由于存在通信延迟，在时刻t，第i个节点接收到相邻的时间信息，该通信模式与实际无线传感器网络中基于包的通信完全兼容。该方法不要求所有节点都具有目标的可观测性，且该限制降低了邻居集的可观测性。

为了将算法的运行时计算开销与集中式和局部估计的运行时计算开销进行比较，协同式、集中式和局部式在每个网络节点的每个采样时间执行的计算浮点运算的次数分别为10τ+2Ni(t)+15、10τ+2N+15和10τ+17，协同式、集中式和局部式的计算开销都很相近，对于高速处理器，基本不会造成其他影响。

3 仿真结果与分析

目标跟踪是传感器网络估计的重要部分，通过数值模拟方法对运动目标进行跟踪，验证算法的可行性。假设目标是平面上的二维运动。在这种情况下，传感器可以分为三组，一组传感器只测量目标位置的第一个维度，另一组传感器测量第二个维度，再一组传感器同时测量两个维度。在通信网络中，传感器与邻居交换信息，并考虑通信延迟和切换拓扑，进行协同估计目标位置，通过实例对运动目标进行定位估计，并将协同估计方法与集中估计和局部估计方法进行比较。

将目标视为点对象，在X-Y平面上运动。在平滑运动的情况下，目标运动模型采用文献[11]中近似恒定速度模型，即：

(28)

式中：ξ(t)为时刻t的目标状态向量，I2×2为二维单位矩阵，w(t)为零均值高斯噪声，采样间隔Δt假定为0.1。

三个节点的协同估计目标位置，则节点处的测量值为：

(29)

(30)

(31)

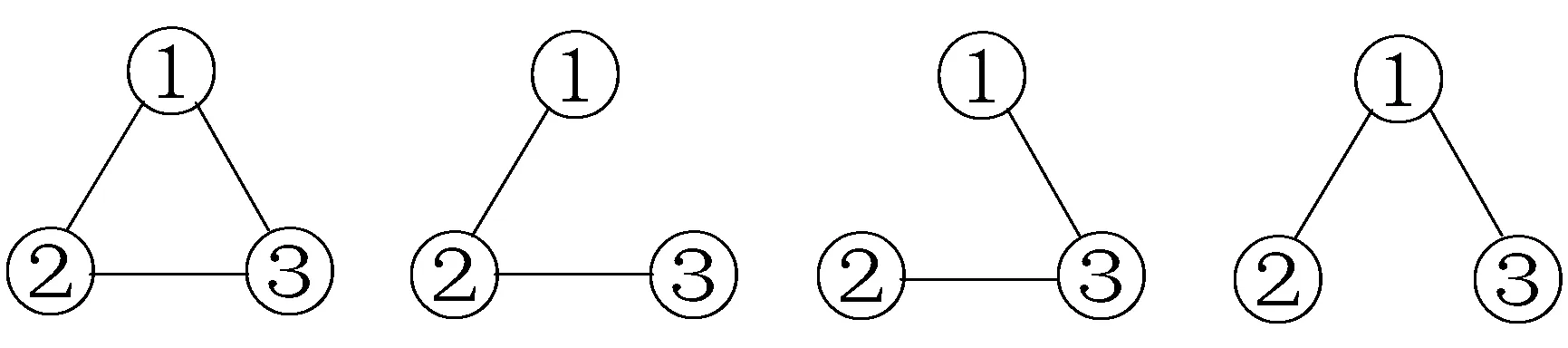
g1 g2 g3 g4图1 传感器网络切换拓扑关系

由式(28)可知，网络的第1个和第2个节点分别测量目标的水平(xt)和垂直(yt)位置，整个目标位置对它们来说是不可观测的。每个节点至少与一个其他节点通信，当相邻节点的信息可用时，则目标位置在每个节点上都是可见的。

将X-Y平面的真实目标位置与协同式、集中式和局部估计进行比较，图2和图3分别为水平位置和垂直位置的比较。可以看出，在局部估计中，网络的第1个和第2个节点分别只能估计目标的水平和垂直位置，因为目标的整个位置矢量对于它们是不可观察的，而对于第3个节点它们是可观察的。除了第三个节点外，其他两个节点无法在局部估计目标的整个位置向量，因此，局部估计仅适用于只适用于目标系统的整个状态向量都是可见的传感器。然而，通过本文中的算法，所有网络节点估计目标的整个位置矢量，且每个节点的整个目标系统的可观察性要求被降低到该组相邻节点的可观察性一致。在准确性方面的最佳估计是集中估计，然而，由于通信限制，对于大多数实际应用是无法实现的。

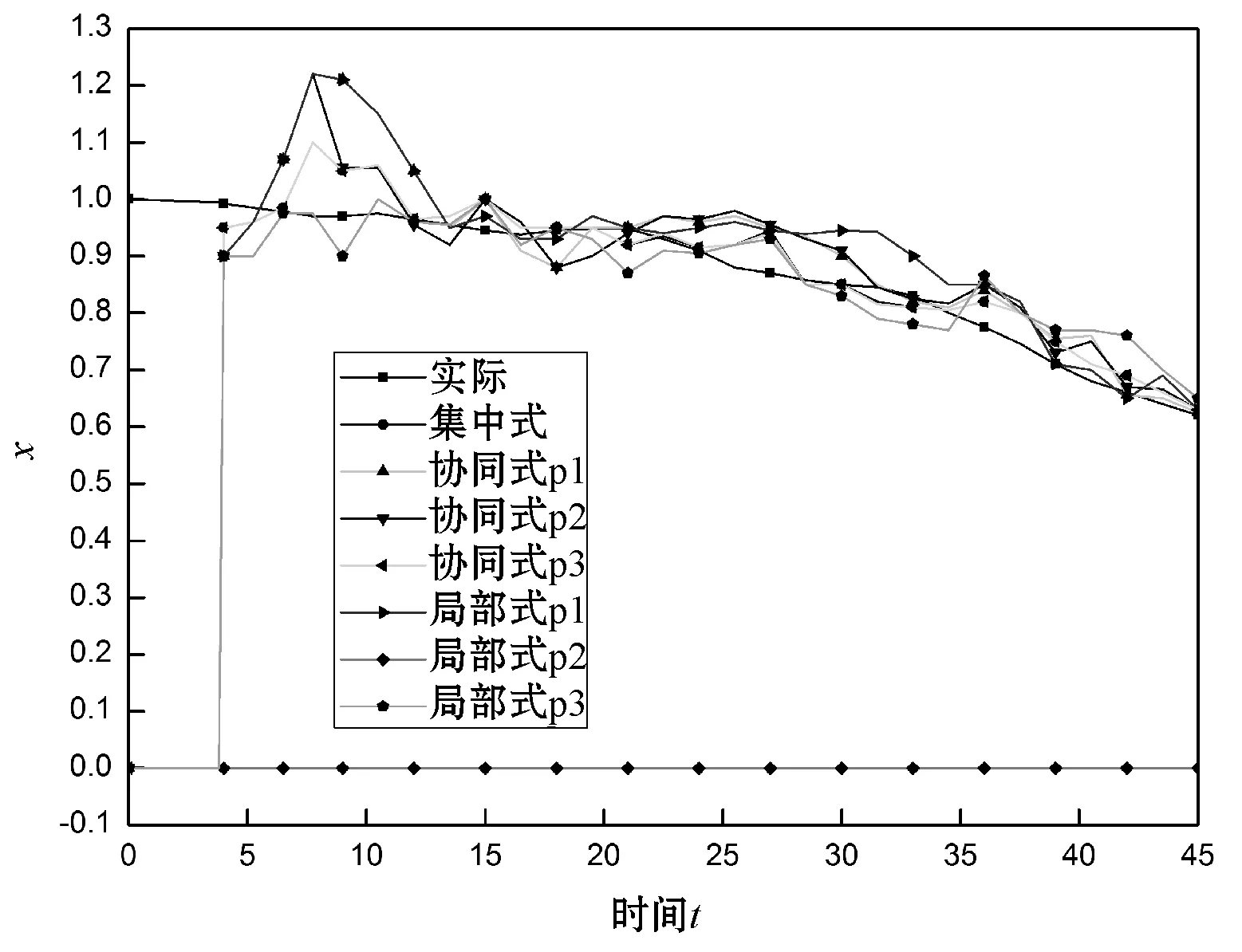
图2 水平位置对比

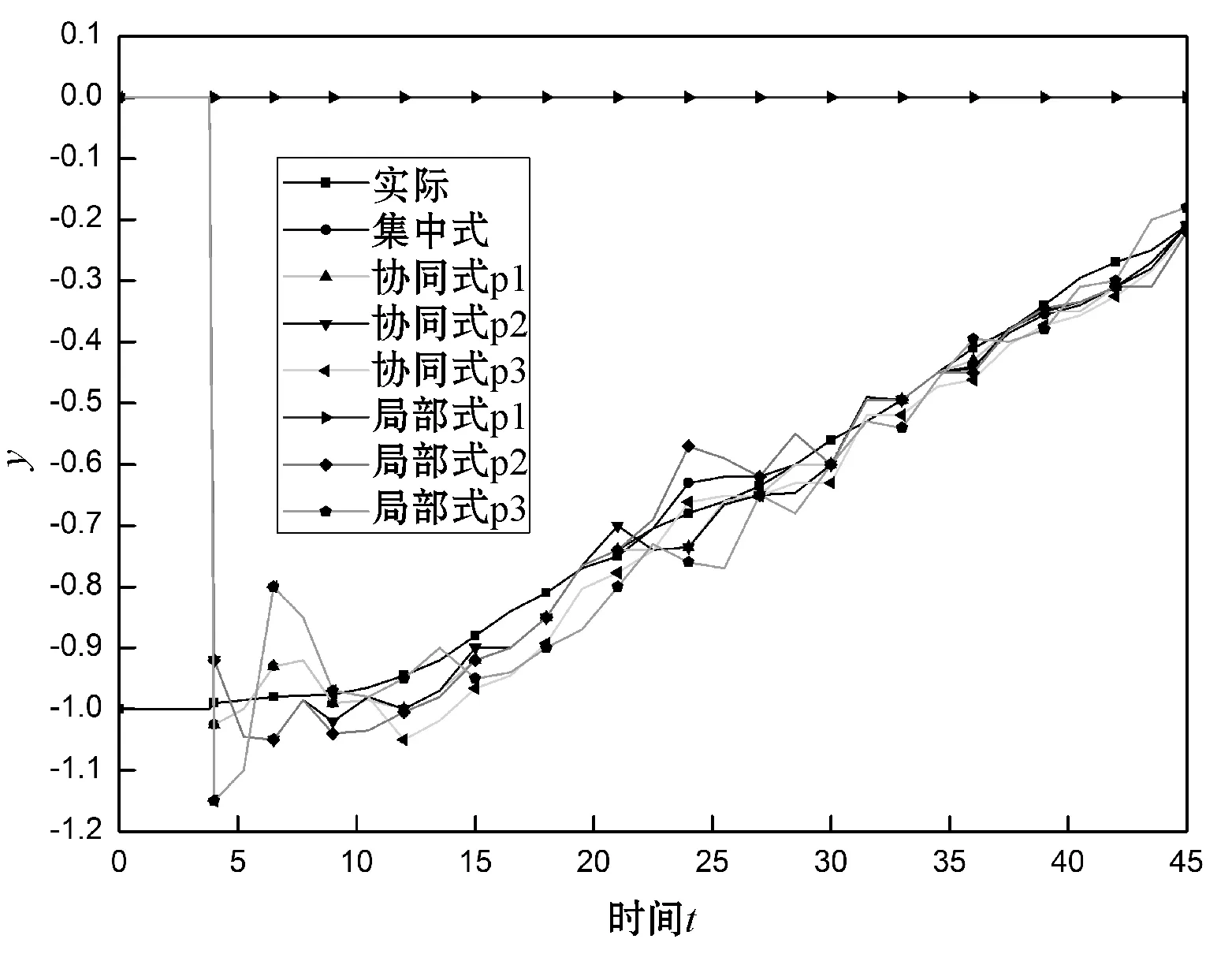
图3 垂直位置对比

本文中的估计方法的性能非常接近集中估计，而不需要满足集中式方法的通信要求。图4为三种方法的估计误差协方差，由图可知，第1个和第2个节点的局部位置估计不准确，并且相关的误差协方差是累积的，原因在于目标对于这些网络节点是不可观察的，因此，局部估计不能有效地进行估计，而本文中的估计方法与集中式估计方法非常接近，进而验证了所提出的方法的有效性。

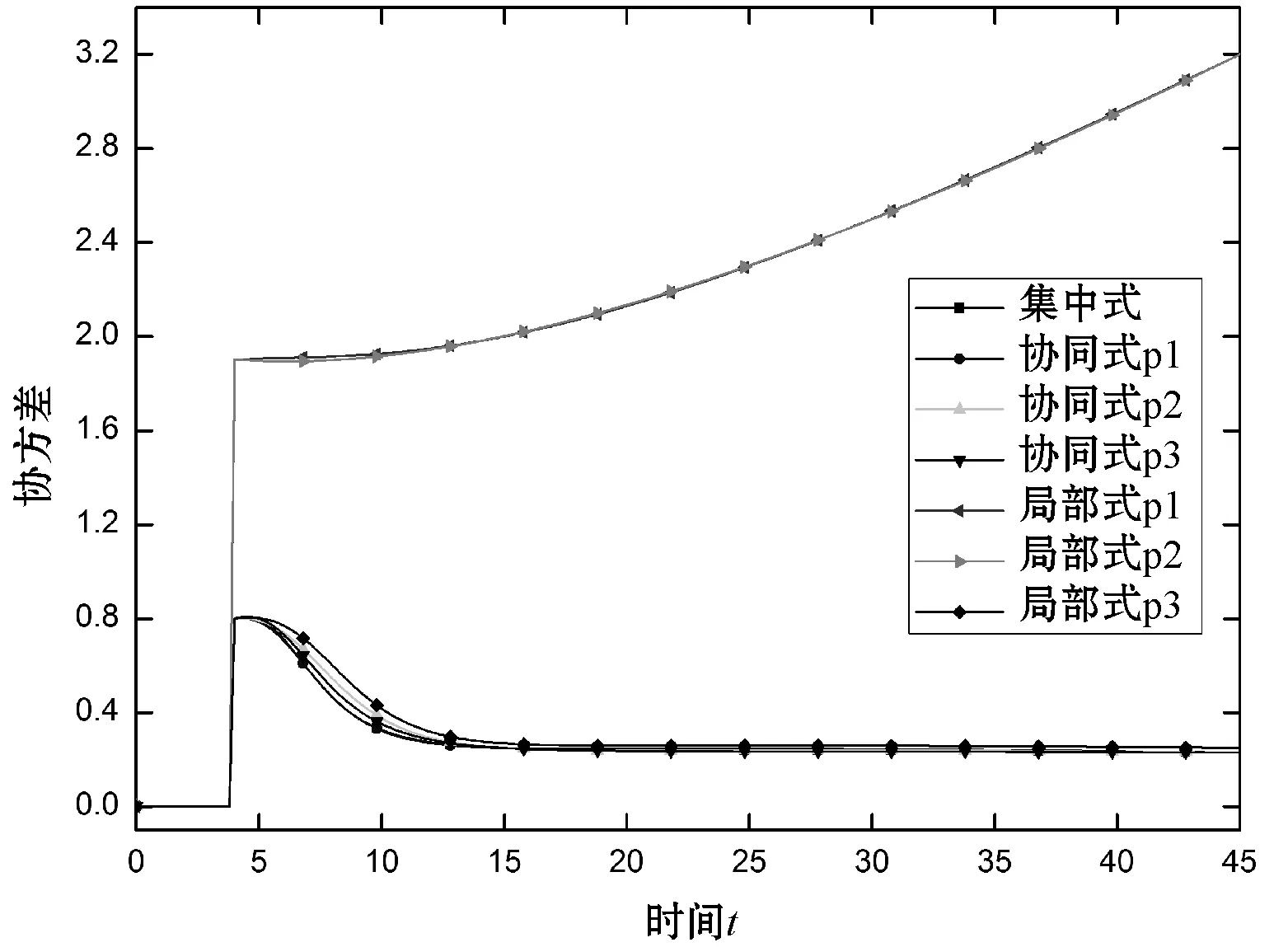
图4 协方差对比

为验证该算法的可行性，采用NS-2仿真软件，分别对模拟退火算法[12]( Simulate Annealing Arithmetic，SAA)、修正定位算法[9]和本文中的协同式算法进行对比。通过在100 m×100 m的区域内随机不熟传感器节点形成无线传感器网络，信标节点个数分别为5/10/15/20/25/30/35/40，仿真次数100次。对比三种算法的定位覆盖率和定位误差与节点密度和节点总数之间的关系。

图5为节点定位覆盖率和信标节点密度的关系曲线，由图可知，无线传感器网络中节点覆盖率随着节点密度变大而增大，模拟退火算法是集中式的定位算法，其通信开销大，能耗大，CLACF算法是基于协同过滤的定位算法，可将其他相邻节点作为参考；而本文中算法对节点要求较低，对所有节点的依赖性相对较小，协同式算法在覆盖率方面分别高于SAA算法和CLACF算法6.1%和4.8%。图6为节点数和定位误差之间的关系曲线，由图可知，当信标节点密度一定时，节点定位误差随着节点数量的增加而减小，当网络节点数量较少时，协同式算法的定位误差均小于SAA算法和CLACF算法，原因在于协同式不需要知道所有节点的信息。在相同的网络环境下，协同式算法的定位误差分别比SAA算法和CLACF算法的定位误差降低了7.7%和3.8%。由此可知，本文中提出的协同式算法的节点定位精度相对较高。

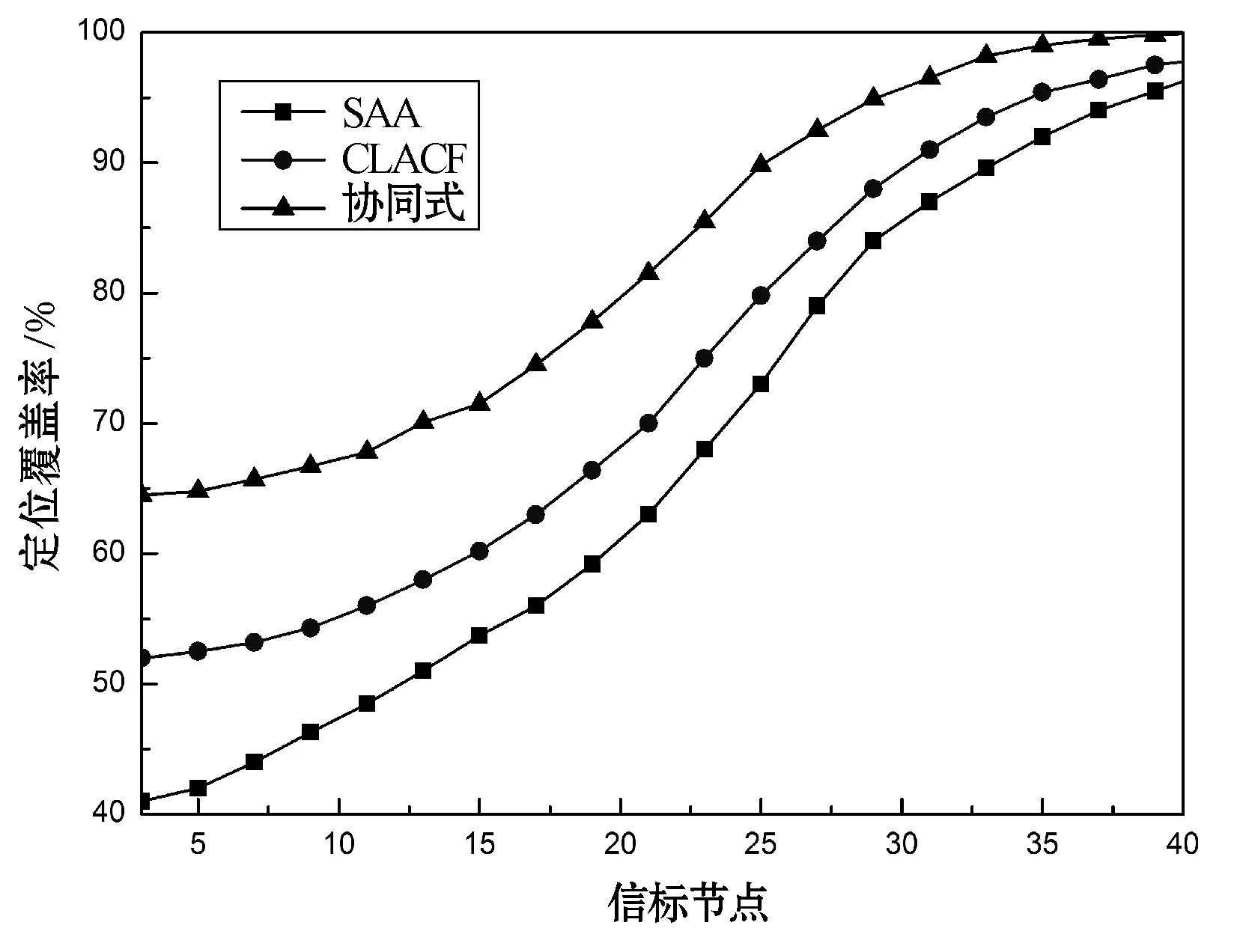
图5 定位覆盖率对比

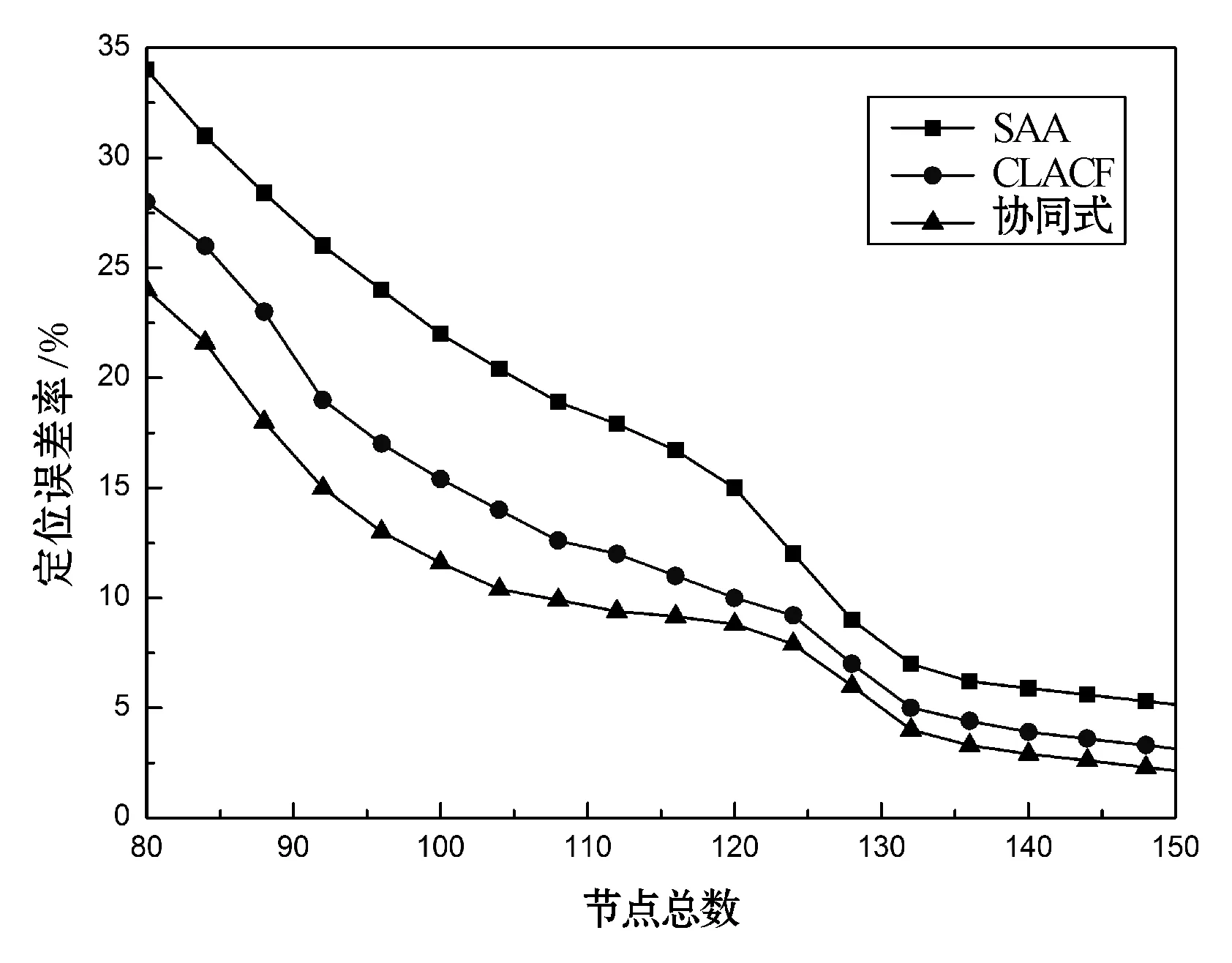
图6 定位误差率对比

4 结 语

本文提出了一种基于通信延迟和切换拓扑的传感器网络状态估计方法。通过本方法，目标系统的状态由每个节点估计，而不需要知道所有节点的信息；该方法不要求目标系统对每个单独的节点都具有可观测性，只需要对每个传感器节点及其相邻节点集具有可观测性即可。该方法估计误差的协方差比局部估计的协方差小，且不受通信限制，其性能与集中估计方法相近。实验对比了SAA算法、CLACF算法和协同式算法，结果表明，协同式算法定位覆盖率和定位精度均较优，可适用于大型移动网络和可能出现通信故障的网络。