具有心理效应的随机扰动捕食-食饵模型

陈哲文,魏春金,张树文

(集美大学理学院，福建 厦门 361021)

0 引言

捕食-食饵模型一直是生态学和生物数学的重要研究内容，有很多文献研究了该模型,并获得了很好的研究成果[1-4]。众所周知,心理效应[4-6]也会对种群的持久和灭绝造成一定影响。当捕食者在某一区域聚集过多时,就会给食饵带来一定的心理影响,导致其不太愿意在该区域出现。由此,提出了以下模型

(1)

其中：x(t),y(t)分别表示食饵和捕食者在t时刻的种群密度;模型的所有参数都是正的;r1,r2分别表示食饵和捕食者的内禀增长率;a1表示食饵种群的密度制约系数;b1是捕食者对食饵的捕获率;b2与b1有相似的意义;y(t)/f(y(t))可以用来描述“心理效应”[5],其中,y(t)/f(y(t))满足以下2个条件：1)y(t)/f(y(t))>0;2)y(t)/f(y(t))在(0,ξ)单调递增,在[ξ,+∞)单调递减。

食饵x(t)会随着y(t)/f(y(t))的增加而减少。y(t)/[ax(t)]是Leslie-Gower 项,Aziz[3]指出，它是衡量捕食者y(t)随着它最喜欢的食饵x(t)的稀缺而减少。在食饵x(t)严重稀缺的情况下,捕食者y(t)有其他替代的食物来源,但它的增长仍将受到其最喜爱的食物x(t)数量不足的限制。这种情况可以通过在分母上加上一个正常数k2来处理。因此,式(1)的方程变为dy(t)=[(r2-b2y(t))/((x(t)+k2))y(t)]dt。此外,在现实生态系统中,各种形式的环境干扰都是无时不在、无处不在的,种群的增长率经常受到随机波动的影响。一般来说,环境中的随机波动可以用白噪声来描述[7]。于是,得到了下述模型:

(2)

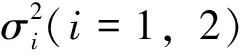
1 预备知识

a.s.:=几乎处处,trA(A是矩阵):=矩阵A的秩。

初值为X(t0)=X0的d维随机微分方程

dX(t)=f(X(t),t)dt+g(X(t),t)dB(t),t0≤t≤T。

(3)

设X(t)(t≥0)是方程(3)的解,V∈C2,1(Rn×R+;R),则V(X(t),t)仍是It过程,具有随机微分dV(X(t),t)=(Vt(X(t),t)+VX(X(t),t)f(t)+1/2 tr[gT(t)VXX(X(t),t)g(t)])dt+VX(X(t),t)g(t)dB(t),a.s.,称此式为It公式[8]。

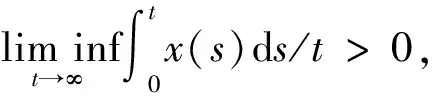
引理1[4](存在唯一性定理) 假设f(x(t),t),g(x(t),t)关于x(t)满足以下条件:ⅰ)局部Lipschizt条件，存在ck>0(k=1,2,…),使得对∀x,y∈Rn且|x|∨|y|≤k,有不等式|f(x,t)-f(y,t)|∨|g(x,t)-g(y,t)|≤ck|x-y|成立;ⅱ)线性增长条件，存在c>0,使得|f(x,t)|∨|g(x,t)|≤c|1+|x||,∀(x,t)∈Rn×R+,则初始条件为x(0)=x0∈Rn的系统(3)存在唯一连续的局部解x(t),t∈[0,τe),其中τe是爆破时。

引理2[10]考虑下列随机微分方程

dX(t)=X(t)[r1-a1X(t)]dt+σX(t)dB(t),

(4)

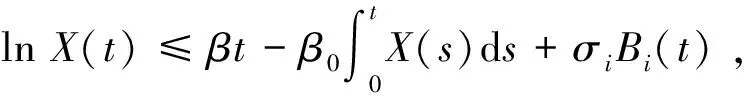
2 主要结果

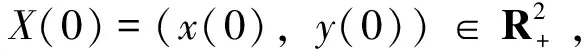
证明令u(t)=lnx(t),v(t)=lny(t)。由It公式可得

(5)

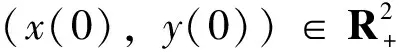
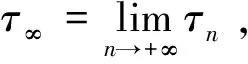
dV(x(t),y(t))=LVdt+(x-1+xy)σ1dB1+(xy-1+k2y)σ2dB2,

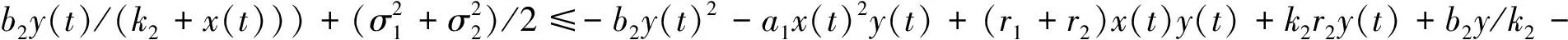
让Ωn={τn≤T},当n≥n1时,由上述P(τn≤T)≥ε,∀n≥n1,有p(Ωn)≥ε。由停时的定义,把n和1/n代入V(x(t),y(t)),易得V(x(T∧τn),y(T∧τn))≥min{n-lnn-1 ,1/n+lnn-1,-lnn+(k2+n)n-(1+lnk2),lnn+(k2+1/n)1/n-(1+lnk2)}:=Q。则V(x(0),y(0))+MT≥E(V(x(T∧τn),y(T∧τn)))=E(1Ωk(λ)V(x(T∧τn),y(T∧τn)))≥εQ。其中,1Ωk(λ)是Ωk的指标函数。令n→∞，得到∞>V(x(0),y(0))+MT=∞,与假设矛盾，即τ∞=∞,a.s.。证毕。

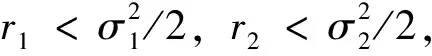
证明ⅰ)对lnx(t)应用It公式可得

(6)

两边同时从0到t积分

(7)

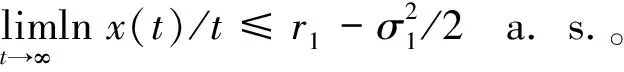
对lny(t)应用It公式可得两边同时从0到t积分

(8)

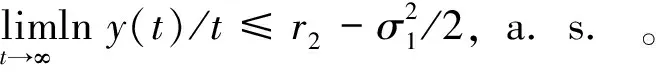
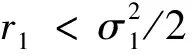
(9)

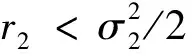
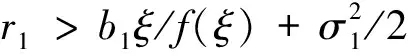
(10)

3 数值模拟

为了验证结果的正确性,采用Milstein高阶方法[11]对随机系统(2)进行数值模拟。取f(y)=1+αy(t)2,α是测量心理或抑制作用的参数。显然它满足y(t)/f(y(t))在y(t)较小的时候递增,在y(t)较大的时候递减。另取r1=0.4,r2=0.3,k2=1,b2=0.3,b1=0.4,a1=0.1和初值(1,0.8),通过取不同的σ1,σ2,α来研究白噪声和心理效应对系统(2)的影响。

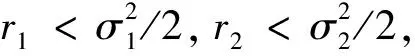
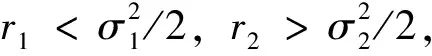
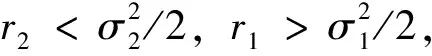
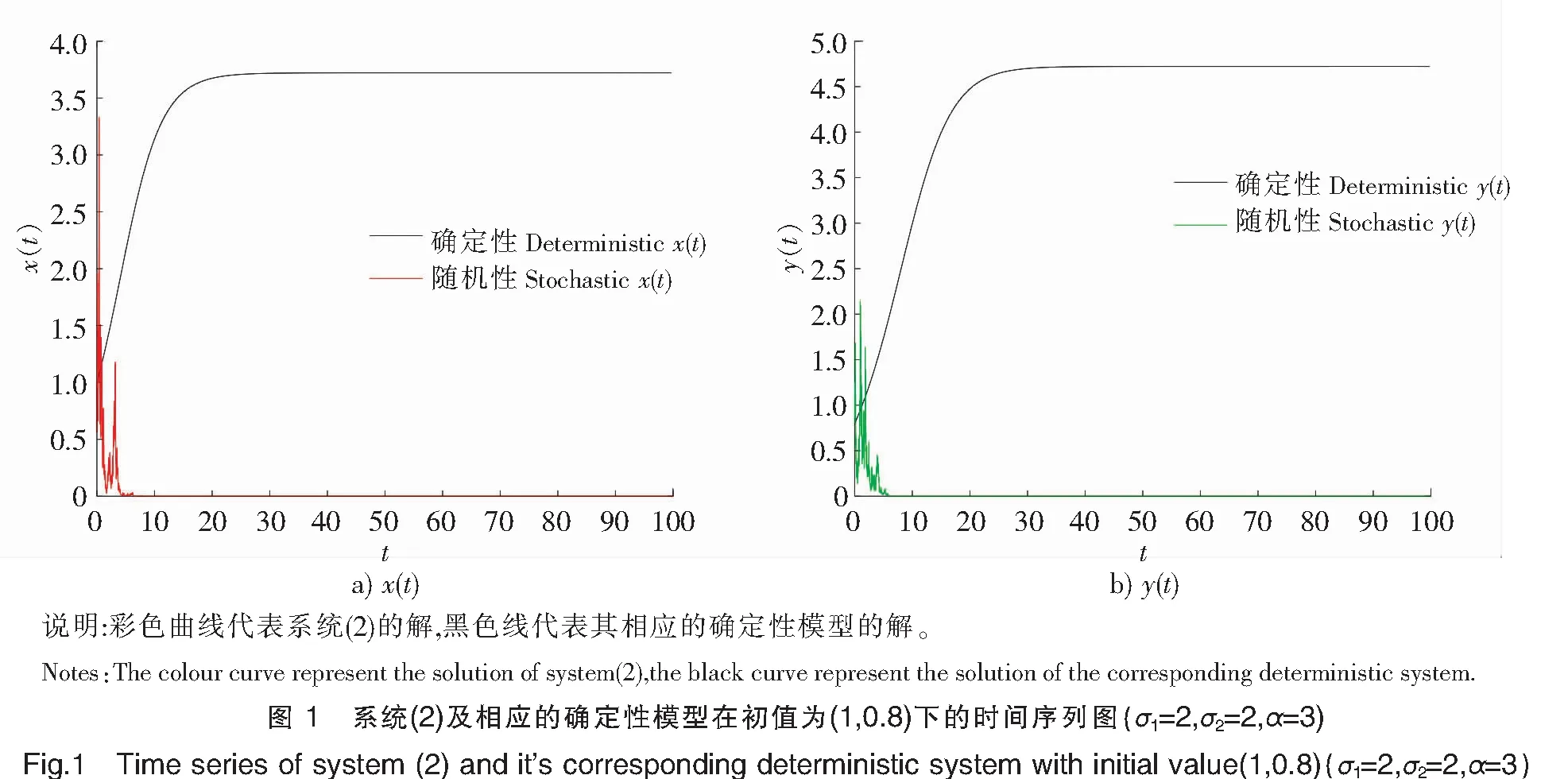
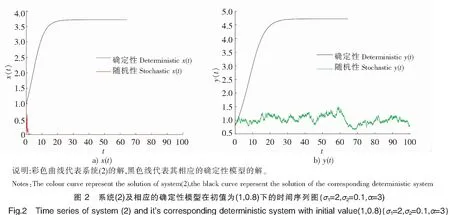
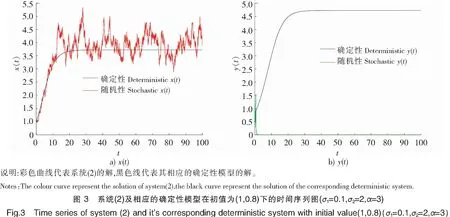
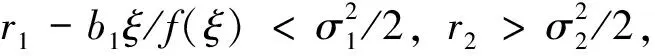
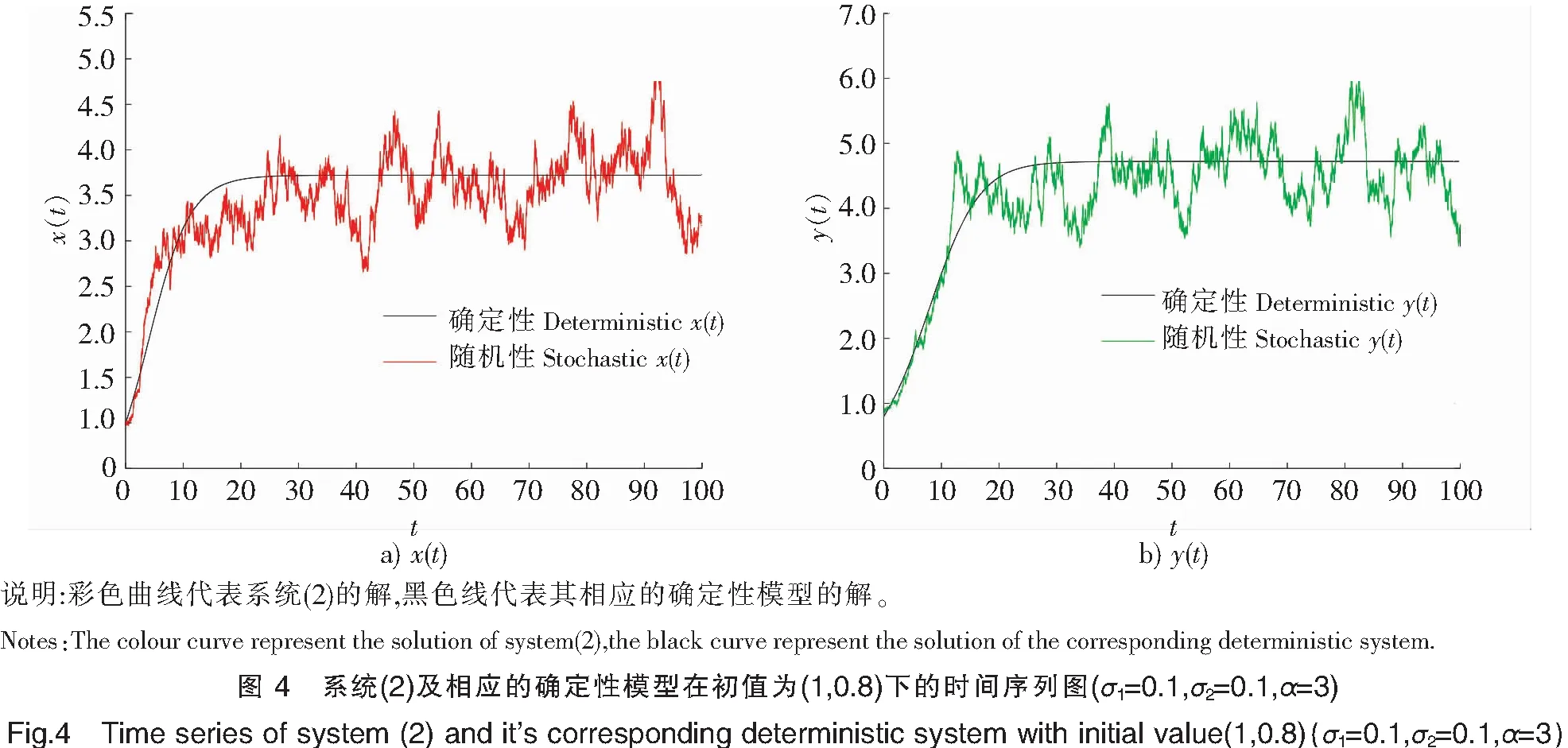
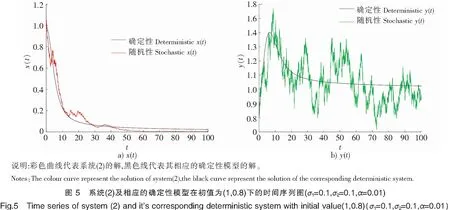
比较图1、图2可以发现,当σ1与α不变,σ2变动时,种群x(t)始终灭绝,而种群y(t)则由灭绝变为平均持续生存。比较图1、图3可以发现,当σ2与α不变,σ1变动时,种群x(t)由灭绝变为平均持续生存,而种群y(t)始终灭绝。由此可知,白噪声过大时,种群趋于灭绝；白噪声较小时,种群可以平均持续生存。而将图4与图5进行比较,当σ1与σ2均不变,将α的取值改变,在“心理效应”较小的时候,种群x(t)是平均持续生存的,在“心理效应”较大的时候,则种群x(t)趋于灭绝。而种群y(t)始终是平均持续生存的。可以看出，心理效应也会对种群x(t)的平均持续生存和灭绝造成一定影响,即较强的心理效应不利于种群x(t)的生存。

4 结论

本文研究了具有心理效应的随机扰动捕食-食饵系统。通过构造合适的Liapunov函数并运用It公式,证明了系统(2)全局正解的存在唯一性，给出了种群x(t),y(t)灭绝与平均持续生存的充分条件。最后通过数值模拟验证结果的正确性,得到：随机扰动对种群的生存与灭绝扮演着重要的角色,当白噪声较大时,种群x(t),y(t)更快地趋于灭绝;当白噪声较小时,种群x(t),y(t)相对缓慢减少,并持续生存;种群x(t)也会受到心理效应的影响,当心理效应较大时,种群x(t)会不太愿意在该区域出现,从而导致数量减少。